Задача 2. Оценка дуговой эластичности

Для стимулирования сбыта своей продукции фирма — производитель молочной продукции объявила о снижении цен на одну из разновидностей йогуртов с 24 до 18 руб. за упаковку. В результате за две недели компания увеличила объем продаж с 10 тыс. до 18 тыс. ед. продукции.

Оценим эластичность потребительского спроса по методу дуговой эластичности.

Прирост спроса Q₂ — Q₁ = 18 — 10 = 8 тыс. ед.

Средняя величина спроса (Q₁ + Q₂)/2 = (10 + 18)/2 = 14 тыс. ед.

Прирост цены P₂ — Р₁ = 18 — 24 = - 6руб.

Средний уровень цены (Р₁ + P₂)/2 = (18 + 24)/2 = 21 руб.

Таким образом, E_d = (8/14) : (-6/21) = -2.

Экономический смысл полученного коэффициента:

Снижение цены на йогурт на 1% ведет к увеличению спроса на 2%.

Использование формулы дуговой эластичности при всей простоте и привлекательности дает лишь приблизительное значение коэффициента эластичности. Погрешность будет тем больше, чем значительнее прирост рассматриваемых парамет­ров.

По характеру эластичности рыночных показателей приня­то выделять три возможных случая в зависимости от абсолют­ной величины коэффициента эластичности (Е).

Если абсолютная величина коэффициента эластичности 0 < |Е| < 1, то говорят о неэластичности спроса или предложе­ния — темпы роста рассматриваемого параметра меньше тем­пов изменения воздействующего на него фактора.

Если |Е|=1, то имеет место единичная эластичность — рас­сматриваемый параметр растет теми же темпами, что и другой фактор.

Если |Е| >1, то спрос или предложение считаются эластич­ными — параметр растет более высокими темпами, чем изменя­ется другой фактор.

Кроме того, в теоретических моделях могут рассматривать­ся ситуация абсолютной неэластичности параметра (Е = 0), ко­гда изменение какого-либо параметра рыночной конъюнктуры вообще не оказывает влияния на величину рассматриваемого показателя, и ситуация абсолютной эластичности (Е = (∞). Впоследнем случае даже незначительное изменение какого-либо параметра повышает (или понижает) значение другого фактора на неограниченно большую величину.

На рис. 1. представлены два основных типа кривых спроса.

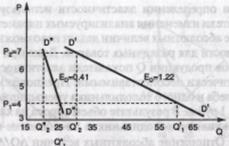
Рис. 1. Эластичность спроса по цене: D'D' — эластичный спрос; D'D" — неэластичный спрос

В первом случае (рис. 1.35 D'D') малейшее увеличение цены вызывает резкое падение объема спроса. Спрос, гибко и чувствительно реагирующий на изменение цены, называется эластичным, а соответствующие товары называются товарами с эластичным спросом. Во втором случае (рис. 1. D"D") даже значительное увеличение цены вызывает лишь небольшое снижение объема спроса, что соответству­ет неэластичному спросу на товар. К товарам с неэластичным спро­сом относятся, например, товары первой необходимости, которым нет замены, а также товары с ажиотажным спросом, скажем, цветы накануне 8 Марта.

Из определения эластичности и приведенных выше фор­мул можно вывести два важных свойства эластичности.

Первое свойство: эластичность (в отличие от производной) — безразмерная величина, значение которой не зависит от того, в каких единицах мы измеряем объем, цены или какие-либо другие параметры.

Предположим, что на рынке кофе повышение цены на 10 руб. за кг сократило объемы суточного потребления кофе на 40 кг. Дадим оценочные данные производной функции спроса по цене:

dQ/dp = — 40 кг/10 руб./кг = — 4 (кг²/руб.).

Аналогичным образом оценим производную спроса на элек­троэнергию. Предположим, что мы имеем

dQ/dp = — 0,08 (квт/ч/руб.).

Полученные для различных товаров производные являются несопоставимыми по единицам измерения, а их сравнение — экономически бессмысленным. Если же мы оцениваем эла­стичность, то размерности сокращаются, и это позволяет ана­лизировать и сравнивать реакцию покупателей и продавцов на различных товарных рынках.

Второе свойство: эластичности взаимно обратных функций являются взаимно обратными величинами.

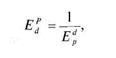
где Ed — коэффициент эластичности спроса по цене, Е_р — коэффициент эластичности цены по спросу. Поясним вышеизложенное на материале конкретной за­дачи 3.3.