Предельные случаи теоремы Паскаля

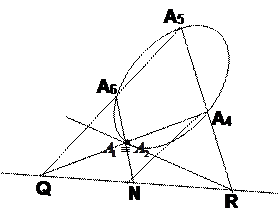Если одна из вершин шестивершинника перемещается по квадрике и совпадает с соседней вершиной, то их рассматривают как две вершины шестивершинника, и прямая, проходящая через эти две точки, будет отдельной стороной шестивершинника.

Определение 9.4. Фигура которая получается при совпадении двух вершин (фактически она состоит из пяти точек и шести прямых) называется предельным шестивершинником.

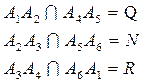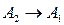Пусть . Противоположные стороны:

Каждый предельный шестивершинник определяет конфигурацию Паскаля, причем каждая конфигурация предельного перехода может быть закреплена соответствующей теоремой.

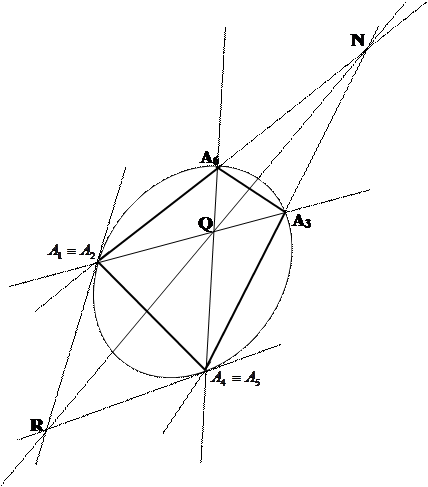Теорема 9.5 ( ). Для того чтобы прямая касалась квадрики, определяемой данными пятью точками, необходимо и достаточно, чтобы для предельного шестивершинника, определенного данными точками и прямой, выполнялись требования теоремы Паскаля.

Теорема 9.6( ) Пусть четыре точки, из которых никакие три не лежат на одной прямой, и прямая проходящая через одну и только одну из них. Для того чтобы прямая касалась квадрики, определяемой данными четырьмя точками, необходимо и достаточно, чтобы для предельного шестивершинника, определенного данными точками и прямой, выполнялись

требования теоремы Паскаля.

Теорема 9.7. ( ) Пусть четыре точки из которых никакие три не лежат на одной прямой, и прямая проходящая через одну и только одну из них. Для того чтобы прямая касалась квадрики, определяемой данными четырьмя точками, необходимо и достаточно, чтобы для предельного шестивершинника, определенного данными точками и прямой, выполнялись требования теоремы Паскаля.

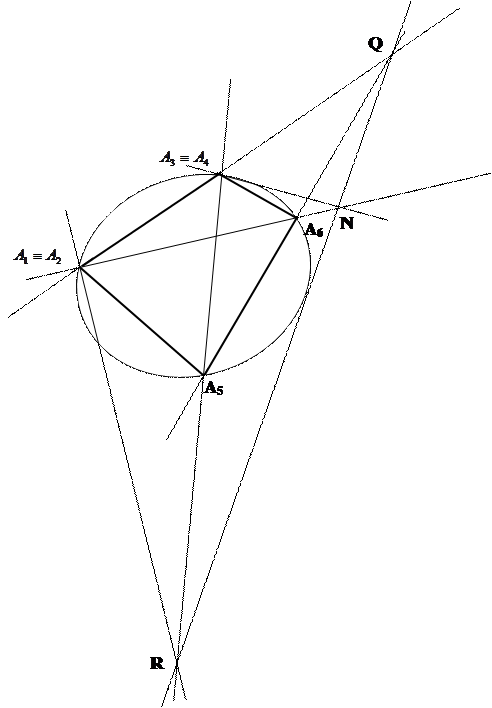Теорема 9.8.( 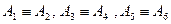). Пусть три точки, из которых никакие три не лежат на одной прямой, и прямая проходящая через одну и только одну из них. Для того чтобы прямая касалась квадрики, определяемой данными тремя точками, необходимо и достаточно, чтобы для предельного шестивершинника, определенного данными точками и прямой, выполнялись требования теоремы Паскаля.

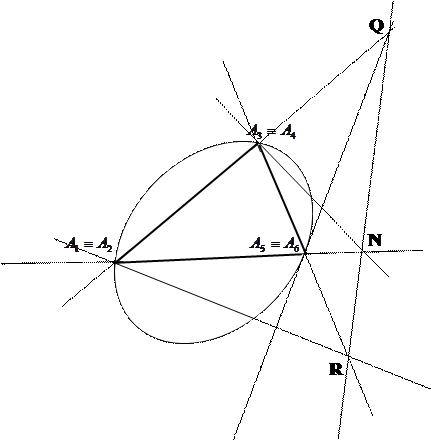
Теорема 9.9 (Теорема Брианшона. Для того чтобы шесть прямых, среди которых нет трех принадлежащих одной точке, касались овальной квадрики необходимо и достаточно, чтобы три прямые соединяющие противоположные вершины шестивершинника, образованного данными прямыми, пересекались в одной точке называемой точкой Брианшона.

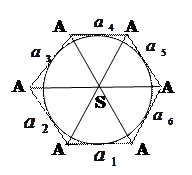В точку Брианшона при полярной корреляции переходит Паскалева ось (прямая, на которой лежат точки пересечения).

Предельные случаи теоремы Брианшона получаются двумя способами:

1) они двойственны предельным случаям теоремы Паскаля;

2) их можно получить путём предельного перехода из самой теоремы Брианшона: смещают две касательные, и точка их пересечения совпадает с точкой касания или является точкой касания.

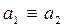I. II.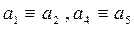

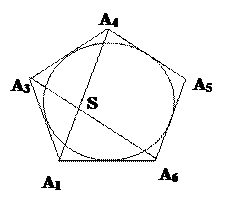
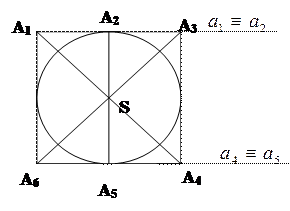
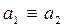
III. IV.

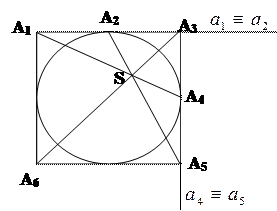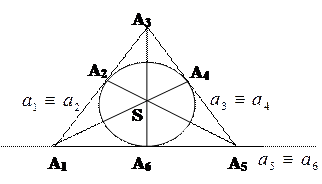Теорема 9.10.(теорема Штейнера). Пусть даны два пучка с центрами О₁ и О₂ и установлено проективное соответствие не являющееся перспективным. Тогда множество точек пересечения соответственных прямых этих пучков является овальной линией второго порядка проходящей через точки О₁ и О₂.

Следствие: Если f – соответствие указанное в теореме Штейнера, то образы прямой О₁О₂ при отображении 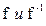являются касательными к овальной квадрике в точках О₁ и О₂.

Теорема 9.11. (обратная теореме Штейнера). Дана овальная квадрика и на ней произвольные точки О₁ и О₂. Каждой прямой О₁М пучка с центром О₁ поставлена в соответствии прямая О₂М пучка О₂. Точка М – произвольная точка не совпадающая с О₁ и О₂. Касательной в точке О₁ поставим в соответствии прямую О₂О₁, а касательной в точке О₂ – прямую О₁О₂. Полученное соответствие является проективным, но не перспективным.

Теорема 7 (об образовании кривых второго порядка посредством проективного отображения одного пучка прямых на другой). Пусть на плоскости даны два пучка прямых с центрами О и О и проективное отображение одного пучка на другой, ставящее в соответствие каждому лучу пучка О луч пучка .

Если отображение не является перспективным, то точки пересечения

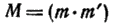
лучей, соответствующих друз другу, при этом отображении лежат на некоторой кривой второго порядка, проходящей через точки О и . Обратно, если на какой-нибудь кривой второго порядка у взяты точки О и и каждому лучу m пучка О ставится в соответствие луч пучка О, идущий в точку пересечения М луча с кривой , то полученное отображение есть проективное отображение пучка О на пучок (очевидно, не являющееся перспективным).

Предположим, что на плоскости дана система однородных координат левые части уравнений всех рассматриваемых далее прямых и кривых второго порядка суть многочлены первой, соответственно второй, степени относительно переменных .

Докажем сначала второе утверждение теоремы 7. Возьмем какие-нибудь два луча пучка О и соответствующие им лучи пучка О (рис. 247). Точки О и лежат на данной кривой второго порядка. Пара прямых есть распадающаяся кривая второго порядка, уравнение которой может быть записано в виде

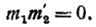(10)

Точно так же пара прямых 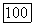есть распадающаяся кривая второго порядка, уравнение которой может быть записано в виде

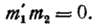
Кривая у проходит через четыре точк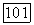и и 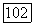каждая из которых принадлежит обеим кривым (10) и (11); поэтому кривая у принадлежит пучку кривых, определенному кривыми (10) и (11).

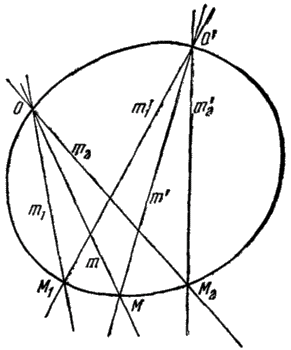
Рис. 247.

Следовательно, уравнение кривой можно записать в виде

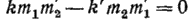
или (помня о возможности заменить через через в виде

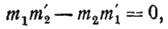
т. е. в виде

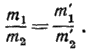
Возьмем теперь в каждом из пучков по проективной системе координат, имеющей лучи 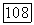соответственно 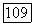своими фундаментальными лучами. Каждая прямая 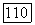пучка О имеет уравнение вида

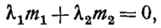
а каждая прямая 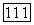пучка О — уравнение вида

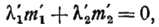
причем 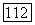соответственно А и 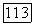суть координаты лучей 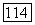в соответствующих координатных системах 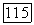. Если прямые 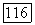соответствуют друг другу в рассматриваемом отображении, то их точка пересечения М принадлежит кривой 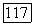, значит, координаты этой точки удовлетворяют уравнению (12). Но эти координаты удовлетворяют и уравнениям (13) и (13).

Подставляя координаты точки М в эти уравнения, получаем равенства

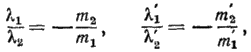
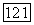правые которых суть определенные числа, равные между собою в силу (12), так что Итак, при нашем отображении пучка О на пучок лучу, имеющему в выбранной в этом пучке координатной системе координаты 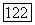соответствует в другом пучке луч, имеющий в соответствующей координатной системе координаты 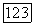Проективность отображения 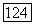этим доказана.

Доказываем первое утверждение теоремы Штейнера.

Пусть между пучками 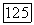установлено проективное соответствие. Тогда при надлежаще выбранных в каждом пучке проективных координатных системах соответствующие друг другу лучи 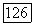обоих пучков имеют пропорциональные пары координат: 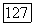и, следовательно, выражаются через координатные лучи 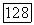соответственно 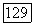одинаковым образом:

Координаты точки пересечения М лучей 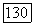удовлетворяют обоим уравнениям 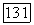и 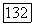, т. е.

Определяя из второго из этих уравнений 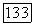подставляя результат в первое уравнение (14), получаем

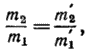
т. е. уравнение

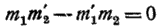
степени не выше второй (относительно 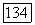). Пусть уравнение (15) — первой степени, тогда оно является уравнением прямой 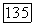, которая оказалась бы осью перспективы для проективного отображения — вопреки нашим предположениям.

Итак, уравнение (15) — второй степени и определяет кривую второго порядка, проходящую через точки 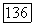. Теорема Штейнера доказана.