Задачи на построение, связанные с овальной линией.

Теоремы Паскаля, Брианшона, Штейнера

Теорема 9.1. (о задании квадрики пятью точками) Каковы бы ни были пять точек проективной плоскости, из которых никакие четыре не лежат на одной прямой, существует единственная квадрика, проходящая через эти точки.

Доказательство

1) Пусть даны A,B,C,D,E , удовлетворяющие условию теоремы, причем А,В,С лежат на одной прямой, а D,E не принадлежат этой прямой. Тогда лишь одна из них, например, точка С может лежать на одной прямой с точками D и Е, а значит из этих пяти точек найдутся четыре точки, не лежащие на одной прямой. Пусть это будут точки А, В, D, Е.

2) Введём проективную систему координат, где точки А, В, D, Е являются базисными.

Так как точки должны принадлежать некоторой квадрике, то их координаты будут удовлетворять уравнению квадрики 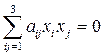, и доказательство будет сводиться к нахождению коэффициентов в уравнении квадрики, с условием, что A,B,C,D,E удовлетворяют ей.

3) Подставляя координаты точек А, В, D в уравнение, получаем: а₁₁=а₂₂=а₃₃=0. Следовательно, уравнение искомой квадрики имеет вид:

а₁₂х₁х₂+а₁₃х₁х₃+а₂₃х₂х₃=0

Подставляя координаты точек Е, С, получаем систему:

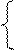
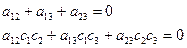
Кроме нулевого решения система имеет единственное решение с точностью до множителя: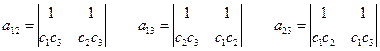

Считая определители, получаем коэффициенты, которые подставляем в уравнение нашей квадрики: .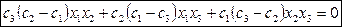

Данное уравнение определяет квадрику.

Определение 9.2. Совокупность шести различных точек, называемых вершинами, и шести различных прямых, называемых сторонами, называется шестивершинником.

А₁А₂А₃А₄А₅А₆ – шестивершинник

А₂А₃ и А₅А₆

А₃А₄ и А₆А₁

А₂ и А₅

А₃ и А₆

Теорема 9.3 (Теорема Паскаля)

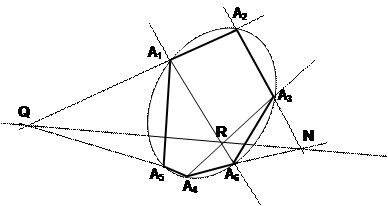
Для того чтобы шесть точек, ни какие три из них не лежат на одной прямой, принадлежали одной овальной квадрике необходимо и достаточно, чтобы точки пересечения противоположных сторон шестивершинника лежали на одной прямой.

Доказать: Q,R,N принадлежат одной прямой.

Доказательство

1) Рассмотрим проективный репер ( А_1, А_2, А_3, А₄ ), тогда А₁(1,0,0), А₂(0,1,0), А₃(0,0,1), А₄(1,1,1). Точка А₅ имеет координаты (с₁,с₂,с₃) и точка А₆(d₁,d₂,d₃). По теореме 9.1 квадрику можно задать уравнением 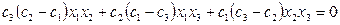. Точки принадлежат квадрике значит уравнение примет вид: 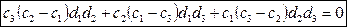- необходимое и достаточное условие принадлежности шести точек одной квадрике.

2) Докажем, что точки N,Q,R принадлежат одной прямой, для этого напишем уравнения прямых А₁А₂ , А₂А₃, А₃А₄, А₄А₅, А₅А₆, А₆А₁ по двум точкам:

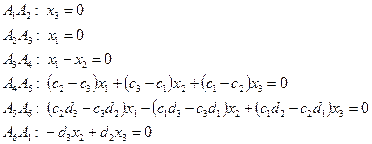
3) Найдем координаты точек пересечения Q,R,N составив системы соответствующих прямых

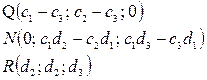
4) Составим определитель из координат точек, и он равен 0. Отсюда следует, что R, N, Q принадлежат одной прямой.