Модель оптимальной партии заказа

Все затраты, связанные с запасами делятся на 3 группы:

- затраты по хранению;

- затраты по размещению заказа на сырье и материалы, их транспортировке и приемке;

- затраты, связанные с нехваткой запасов (падение объема реализации, утрата доверия покупателей, сбои в процессе производства).

Затраты по хранению в основном увеличиваются пропорционально среднему размеру запаса. Величина запасов в свою очередь зависит от частоты их пополнения. Если годовая потребность в сырье составляет S ед. и предприятие заказывает N партий в год, то Q = S/N – величина одного заказа. Если запасы расходуются равномерно, то средний запас рассчитывается по формуле:

А = [S/N]/2.

Затраты по хранению запасов рассчитываются в процентах от среднегодовой стоимости запасов (С). Общие годовые затраты по хранению (ТСС) равны:

ТСС = С Р А,

где Р – покупная цена единицы запаса.

Затраты по размещению и выполнению заказов на сырье и материалы в большинстве случаев не зависят от размера партии, а являются постоянными для одного заказа. Таким образом, общие затраты по выполнению заказов (ТОС) равны:

ТОС = F N = F S / 2A,

где F – постоянные затраты на размещение одного заказа.

Общие затраты по поддержанию запасов (TIC):

TIC = ТСС + ТОС = С Р А + F S / 2A

C ростом среднего размера заказа снижаются затраты по размещению заказа и возрастают затраты по хранению и наоборот. Модель оптимальной партии заказа (ЕОQ – Economic Ordering Quantity) позволяет оптимизировать пропорции между этими группами затрат таким образом, чтобы совокупная их сумма была минимальной:

,

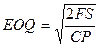F – постоянные затраты на размещение одного заказа;

S – годовая потребность в запасах сырья;

С – годовые затраты по хранению в процентах от среднегодовой стоимости запаса;

Р – покупная цена единицы запаса.

Модель оптимальной партии заказа основана на допущениях:

1) годовая потребность в запасах может быть точно спрогнозирована;

2) объемы реализации равномерно распределены в течение года;

3) не происходит задержек в получении заказов.

Для предотвращения дефицита материальных запасов в случае задержки поставки или непрогнозируемого роста спроса необходимо создавать страховой запас. Если спрос на продукцию предприятия подвержен сезонным колебаниям, то модель EOQ может быть применима для отдельных периодов, в течение которых объемы реализации относительно стабильны.

Для запасов готовой продукции задача состоит в определении оптимального размера партии производимой продукции. Если производить определенный товар мелкими партиями, то операционные затраты по хранению его запасов в виде готовой продукции будут минимальными. Вместе с тем, существенно увеличатся затраты, связанные с частой переналадкой оборудования, подготовкой производства и другие. Используя вместо годовой потребности в сырье показатель планируемого объема производства, аналогичным образом можно использовать модель ЕОQ для определения оптимального среднего размер партии продукции и среднего размера запаса готовой продукции.

Вопрос 6

Цель управления дебиторской задолженностью заключается в оптимизации ее общего размера с учетом динамики объемов реализации и обеспечении своевременной ее инкассации.

Разработке политики управления дебиторской задолженностью предшествует анализ ее состояния, в рамках которого изучается:

а) средний размер дебиторской задолженности и ее удельный вес в составе оборотных активов предприятия;

б) средний период инкассации задолженности в днях;

в) состав дебиторской задолженности по ее видам;

г) состав дебиторской задолженности по ее срокам погашения. Выделяется нормальная, просроченная и безнадежная дебиторская задолженность;

д) «возраст» дебиторской задолженности. Такой анализ углубляет характеристику ее состава по срокам погашения и проводится обычно только в разрезе нормальной дебиторской задолженности.