Группы Ассура и их классификация

Кинематическая цепь, которая после присоединения её всеми свободными элементами кинематических пар к стойке получает подвижность, равную нулю, называется группой Асура. Таким образом,

W_гр.Асс. = 0.

В состав группы Асура входят только кинематические пары 5 класса, поэтому, согласно формуле Чебышёва:

W_гр.Асс. = 3n – 2 p₅ = 0,

откуда получаем 3n = 2p_{5 ,} или p₅ = 3/2∙n, как условие существования группы Ас-

сура. Составим таблицу из нескольких сочетаний количества звеньев и кинематических пар в группах Ассура согласно приведённому выше соотношению

Группы Ассура делятся на классы и порядки.

Класс группы определяется классом наиболее сложного замкнутого контура в составе группы:

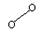
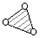
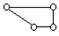
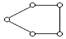
II класс III класс IV класс V класс и т. д.

Кинематические пары в контуре III класса, могут быть расположены по одной прямой, не образуя никакой контур, однако считается, что и в этом случае имеется контур III класса. Порядок групп Ассура определяется количеством свободных элементов кинематических пар, которыми группы Ассура присоединяются к дру 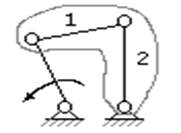гим звеньям.

Рассмотрим несколько примеров групп Ассура и механизмов с этими группами.

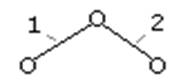
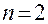
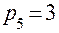
Группа Ассура II класса, 2-го порядка Четырёхшарнирный

1-го вида механизм

Группы II класса делятся также на виды (модификации) в зависимости от количества и расположения в них поступательных и вращательных кинематических

пар. Приведённая выше группа Ассура относится к первому виду. Если в этой группе один из крайних элементов вращательной пары заменить поступательным, то получится группа второго вида. Если заменить среднюю вращательную пару поступательной, то такая группа Ассура получится группой Ассура третьего вида.

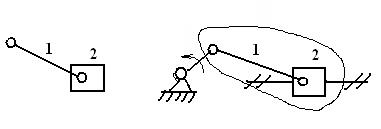
Группа Ассура Кривошипно-ползунный

II класса, 2-го механизм

порядка, 2-го вида

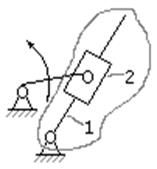
Группа Ассура II класса, Кривошипно-кулисный

2-го порядка, 3-го вида механизм

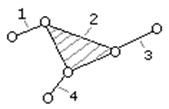
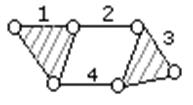n = 4