Классификация по числу условий связей

Классификация плоских кинематических пар

Из курса теоретической механики известно, что свободное твердое тело в про- странстве имеет шесть степеней свободы (рис 1.1). 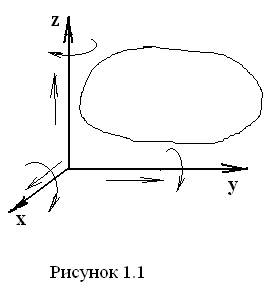Это три поступательных движения вдоль трёх осей координат и три вращательных движения вокруг этих осей. Можно также сказать, что на свободное твёрдое тело не наложено ни одной связи. Если обозначить число степеней свободы буквой H, а

число связей буквой S, то можно записать:

Н = 6, S = 0

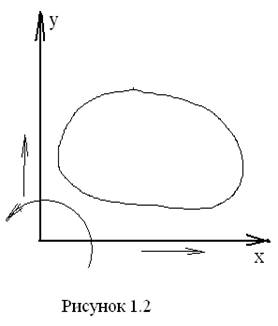
При переходе из пространственной системы в плоскую твёрдое тело теряет три степени свободы, что означает, что на него наложено три связи. Так что свободное твёрдое тело в плоскости имеет H = 3 и S = 3. Например, тело, находящееся в координатной плоскости XY, может двигаться поступательно вдоль этих осей и вращаться вокруг оси, перпендикулярной плоскости XY (рис 1.2).

В плоской кинематической паре количество ограничений в движении звена, называемых условиями связей, может быть или два, или одно.

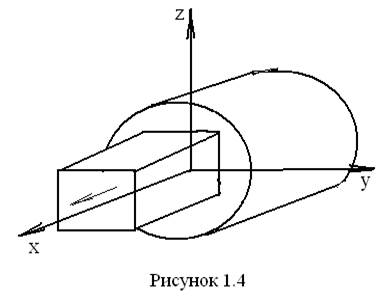
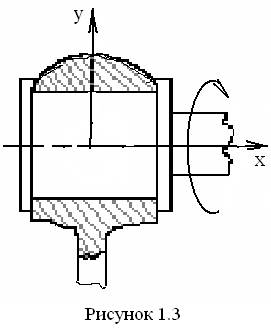
В первом случае общее количество условий связей вместе с тремя потерянными при переходе из пространства в плоскость составляет S = 5. Такая кинематическая пара в соответствии с числом S является парой 5-го класса, а так как в ней может выполняться только одно движение (H = 1), то эта пара называется также одноподвижной кинематической парой. Кинематические пары 5-го класса могут быть вращательными (рис. 1.3) и поступательными (рис. 1.4) в зависимости от характера относительного движения звеньев, реализуемого в ней. Возможные относительные движения звеньев в этих парах на указанных рисунках отмечены стрелками.

Во втором случае общее количество условий связей S = 4, и кинематическая пара является парой 4-го класса, а в соответствии с

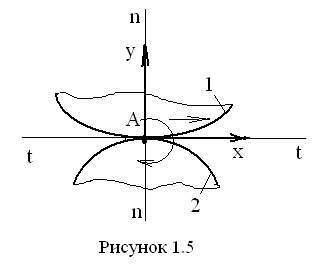
H = 2 она называется двухподвижной кинематической парой (рис. 1.5). Как видноиз этого рисунка, пару 4-го класса в плоскости составляют две кривые 1 и 2, контактирующие друг с другом в точке A. Относительное движение звеньев этой пары возможно в направлении касательной t–t (ось X) и вращение вокруг точки A. Невозможно движение вдоль нормали n–n (ось Y).