ОПЕРАЦИИ НАД СОБЫТИЯМИ.
Сумма (объединение) событий А и В - событие, состоящее в появлении хотя бы одного из событий А и В. Сумму событий обозначают А + В (или А∪В).
Произведение (пересечение) событий А и В - событие, состоящее в их совместном появлении. Произведение событий обозначают А ∙ В (или А∩В).
Разность событий А и В - событие А\В, происходящее тогда и только тогда, когда происходит А, но не происходит В.
|
|
|
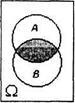
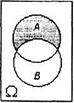
а) А + В б) А ∙ В в) А\В г) Ᾱ
Рис. 6.1
На рис. 6.1 события А + В, А ∙ В, А\В, Ᾱ заштрихованы
Теорема 6.1. Для любых событий Л, В и С справедливы следующие законы и свойства:
1. Коммутативности А + В = В + А; А∙ В = В ∙ А.
2. Ассоциативности: (А • В) • С = А • (В • С); (А + В) + С = А + (В + С).
3. Дистрибутивности: А • (В + С) = (А • В) + (А • С).
4. Идемпотентности: А• А = А; А + А = А.
5. Поглощения. А + Ω = Ω ; А • Ω = А; А +Æ= А; А • Æ = Æ.
6. А+ А = Ω ; А = Ω \А.
7. А + (А •В) = А; А • (А + В) = А.
8.Де Моргана: ⌐ (А•В) = Ᾱ + ; ⌐ (А + В) = Ᾱ • .
9.А\(В•С) = (А\В) • (А\С); А\(В + С) = (А\В) + (А\С) = (А\В)\С/
10.Двойного отрицания: ⌐ Ᾱ = А.
11. А + Ᾱ = Ω;
12. А\В = А • В .
Доказательство этой теоремы опускается.
ВЕРОЯТНОСТЬ СОБЫТИЯ А ( Р(А) ) - отношение числа т благоприятствующих событию А исходов к общему числу п всех равновозможных попарно несовместных элементарных исходов, образующих полную группу, т.е.
Р(А) = m\n (6.1)
Данная формула представляет собой т.н. классическое определение вероятности по Лапласу.
Теорема 6.2. Вероятность достоверного события равна единице: Р(Ω ) = 1.
Доказательство. Пусть Ω - достоверное событие. Тогда в результате испытания оно обязательно произойдет. Следовательно, каждый элементарный исход испытания будет благоприятствующим событию Ω , т.е. m = n. Значит, Р(Ω ) =m\n = 1.Теорема доказана.
Теорема 6.3. Вероятность невозможного события равна нулю: Р(Æ) = 0.
Доказательство. Пусть Æ - невозможное событие. Тогда в результате испытания оно никогда не произойдет. Следовательно, число благоприятствующих событию 0 исходов равно нулю, т.е. m = 0. ЗначитР(Æ) = 0\ n. =0. Теорема доказана.
Теорема 6.4. Если А - случайное событие, то 0 < Р(А) < 1.
Доказательство. Так как А - случайное событие, то в результате испытания оно может как наступить, так и не наступить. Поэтому число m благоприятствующих событию А исходов испытания, с одной стороны, больше нуля, а с другой стороны меньше числа n всех элементарных исходов испытания, т.е. 0 < m < n . Тогда 0/ n < m / n < n / n, и значит,
0 < m / n < 1. Теорема доказана.
Теорема 6.5. Если А - событие, то 0 < Р(А) < 1.
Доказательство следует из теорем 6.2 - 6.4.
Пример 6.5. Испытание состоит в подбрасывании игральной кости, на каждой из граней которой проставлено число очков (от 1 до 6). Какова вероятность того, что: а) выпадет 2 очка? б) выпадет нечетное число очков?
Решение. В данном испытании имеется 6 равновозможных случаев (выпадение 1,2,3,4,5,6 очков, т.е. n = 6), т.к. нет оснований предполагать, что появление какого-то определенного числа очков более вероятно (при условии, что кость симметрична). Поэтому вероятность выпадения любого числа очков, в том числе и 2, при одном (m = 1) подбрасывании равна 1/6.
Событию А, заключающемуся в появлении нечетного числа очков, благоприятствуют три случая (выпадение 1, 3 и 5, т.е. m = 3), поэтому по формуле (6.1) получаем Р(А) = m / n = 0,5.
Ответ, а) 1/6; б) 0,5.
Пример 6.6. В коробке из 12 кубиков находятся 5 красных кубиков. Найдите вероятность того, что среди восьми взятых наудачу кубиков, ровно 2 красных.
Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 8 кубиков из 12, т.е. числу сочетаний из 12 элементов по 6 (С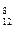 
). Подсчитаем число исходов, благоприятствующих событию А - "Среди восьми взятых кубиков ровно 2 красных": 2 красных кубика можно взять из 5 красных кубиков С 
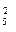способами; при этом остальные 8 ∙ 2 = 6 кубика не должны быть красными; взять же 6 не красных кубика из 12 - 5 = 7 не красных кубиков можно С 
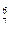способами.
Следовательно, число благоприятствующих исходов равно С 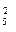• С .
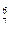Искомая вероятность равна отношению числа исходов, благоприятствующих событию,
к числу всех элементарных исходов: Р(А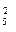) = (С • С 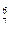) : (С 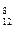) = 14 \ 99.
Ответ: 14/99.
В основе математических моделей, используемых в теории вероятностей, лежат три понятия: пространство элементарных событий Ω, класс событий А (подмножеств Ω) и определенная на этом классе функция множеств Р - вероятностная мера. Значение Р(А) функции Р для события А и называется вероятностью события А.
ОТНОСИТЕЛЬНАЯ ЧАСТОТА СОБЫТИЯ - отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Относительная частота события А определяется формулой W(А) = m\n, где m - число появлений события, n - общее число испытаний.
Определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта. Так, если по окончании экзаменационной сессии выясняется, что из 24 случайно отобранных студентов неуспевающими являются 3 студента, то относительная частота появления неуспевающих студентов W(А) = 3/24 = 0,125.
Длительные наблюдения показывают, что если в одинаковых условиях производятся опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости, суть которое состоит в том, что в различных опытах относительна частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число есть вероятность появления события. Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.
Пример 6.7. По данным статистического управления города N относительная частота рождения девочек за 2000 г. по месяцам характеризуется следующими числами (числа расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473. Относительная частота колеблется около числа 0,482, которое можно принять за приближенное значение вероятности рождения девочек.
СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. Классическое определение вероятности предполагает, что число элементарных исходов испытания - конечно, а элементарные события равновозможные. О равновозможности элементарных исходов испытания судят из соображений симметрии. Так, например, обстоит дело при бросании игрального кубика, когда предполагают, что он имеет идеальную форму правильного многогранника (куба), при извлечении шаров из урны, когда считают, что шары абсолютно одинаковые по форме и неразличимы на ощупь, и т.п.
Однако задачи, в которых можно исходить из соображений симметрии, на практике встречаются весьма редко. Чаще встречаются испытания, элементарные события которых не являются равновозможными. В таких случаях классическое определение неприменимо. По этой причине наряду с классическим определением пользуются также статистическим определением вероятности, принимая за вероятность события относительную частоту или число, близкое к ней. Другими словами, если в результате достаточно большого числа испытаний оказалось, что относительная частота события А весьма близка к числу 0,78, то это число принимают за статистическую вероятность события А, и говорят, что событие А стохастически устойчиво. Например, если при 100 попытках стрелок попал в цель 81 раз, то можно считать, что для него вероятность попадания в цель при данных условиях приблизительно равна 0,81, т.е. относительной частоте попадания.
АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ.
Пусть Ω - пространство элементарных событий некоторого стохастического эксперимента и в Ω выделена система 5 событий, являющаяся алгеброй событий. Это означает, что:
1) Ω Î S;
2) Если А Î S Þ Ᾱ Î S;
3) Если А и В Î S Þ А+ В Î S и А∙ В Î S.
Каждому событию А поставим в соответствие число Р(А) (его вероятность) так, что выполняются следующие свойства:
1 .("АÎ S) [Р(А) ≥ 0].
2. Р( Ω )= 1
3.Если А и В несовместны (АВ = Æ), то Р(А + В) = Р(А) + Р(В).
Тройка (Ω , S , Р) называется вероятностным пространством.
Этот подход позволяет, не обсуждая трудного вопроса о том, откуда известны первоначальные вероятности, если известны вероятности одних событий, вычислить по ним вероятности других, достаточно сложных событий, пользуясь только перечисленными аксиомами. В таком виде аксиоматика теории вероятностей была предложена
А.Н. Колмогоровым.
ГЕОМЕТРИЧЕСКАЯ МОДЕЛЬ ТЕОРИИ ВЕРОЯТНОСТЕЙ. Рассмотрим опыт, состоящий в бросании случайным образом точки на отрезок [а; b], предполагая, что попадания в любую точку равновозможны. Пространство элементарных событий Ω в этом опыте - все точки отрезка [а; b]. Поскольку множество элементарных событий несчетно (бесконечно) и все они равновозможны, то для "w Î Ω Р(w ) = 0. Так что классическая схема неприменима. В этом случае положим, что вероятность события А - "Попадание брошенной точки на отрезок [с; d] Ì [а; b] -пропорциональна длине отрезка [с; d] , т.е. Р(А) = к ∙ (d - с), где d - с - длина отрезка. Коэффициент к находится из условия нормировки: Р(Ω ) = к ∙ (а - b) = 1 => к = 1 / (а - b) и Р(А) = (d - с ) / (а - b).
Пример 6.8.Абонент ждет телефонного вызова в течение одного часа. Какова вероятность, что вызов произойдет в последние 20 минут этого часа?
Решение. Пусть событие А состоит в том, что вызов произошел в последние 20 минут. Изобразим пространство элементарных событий в виде отрезка длины 60. Тогда элементарные события, благоприятные А, заключены в последнюю треть отрезка, следовательно, Р{А) =1/3.
Ответ: 1/3.
Естественно, что вместо отрезка можно говорить о плоской фигуре, определив вероятность как отношение Р(А) = S(А) / S (Ω), где S(А) иS (Ω) - площади cоответствующих фигур.
Нетрудно убедиться, что все аксиомы и в том, и в другом случае выполняются.
Пример 6.9.Два лица Х и У условились встретиться в определенном месте между 12 часами и часом, при этом пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц X и У, если приход каждого из них в течение указанного часа может произойти случайно, и моменты прихода независимы?
Решение. Обозначим момент прихода лица X через х, а лица У - через у. Для того, чтобы встреча произошла, необходимо и достаточно выполнение неравенства |х - у| < 20. На координатной плоскости множество точек, удовлетворяющие этому неравенству, изоб 
разятся в виде полосы (рис. 6.2, а), все возможные исходы - точками квадрата со стороной 60 (минут) а благоприятствующие встрече - расположатся в заштрихованной области (рис. 6.2, 6). Следовательно, искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата, т.е. равна (602 - 402 )/602 = 5/9.
у* >
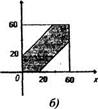
Рис. 6.2
Ответ: 5/9.
ВЕРОЯТНОСТИ СУММЫ И ПРОИЗВЕДЕНИЯ СОБЫТИЙ. Часто бывает так, что вероятность некоторого события можно найти, зная вероятности других событий, связанных с этим событием.
Теорема 6.6. (Теорема сложения вероятностей). Вероятность суммы (объединения; появления одного из них, безразлично какого) двух произвольных событий равна сумме вероятностей этих событий за вычетом вероятности их совместного появления, т.е.
Р(А + В)= Р(А) + Р(В)– Р(АВ).
Доказательство. Пусть А и В - произвольные события. Обозначим через п число всех элементарных исходов испытания, в результате которого может наступить событие А + В. В силу определения число т всех исходов, которые благоприятствуют событию А + В, можно посчитать следующим образом: к числу m₁, благоприятствующих событию А исходов испытания прибавим число т2 благоприятствующих исходов событию В. Поскольку наступление события А + Впроисходит и при совместном наступлении событий А и В (т.е. при наступлении события АВ), а каждый благоприятствующий событию АВ исход благоприятствует как событию А, так и событию В, то в сумме m₁ + т2 дважды учтено число т₃ всех благоприятствующих событию АВ исходов. Поэтому m = m₁ + т2 - т₃ и значит, Р(А + В) = т\п = (m₁ + т2 - т₃ )\п = m₁\п + т2\п - т₃ \п . Учитывая, что m₁\п, т2\п, т₃ \п - вероятности событий А, В, АВ соответственно, то Р(А + В) = Р(А) + Р(В)- Р(АВ). Теорема доказана.
Следствие 1.Вероятность суммы (объединения) попарно несовместных событий равна сумме их вероятностей, т.е. Р(А₁+ А2 +... + Ап) = Р(А₁) + Р(А2) +…+ Р(Ап).
Следствие 2. Пусть А₁, А2, ... , Ап - полная группа попарно несовместных событий. Тогда Р(А₁) + Р(А2) +…+ Р(Ап) =1.
Следствие 3. Сумма вероятностей противоположных событий равна единице, т.е. Р(А) + Р(Ᾱ ) = 1.
Пример 6.10.В урне 5 белых, 6 черных и 9 красных шаров. Какова вероятность того, что первый наугад вынутый шар окажется черным или красным?
Решение. Здесь имеется всего 20 элементарных исходов, из которых появлению черного шара благоприятствует 6, а появлению красного - 9. Поэтому вероятность события А - появление черного шара: Р(А) = 6/20, а вероятность события В - появление красного шара: Р(В) = 9/20. Поскольку события А и В несовместны (вынимается всего один шар), то Р(А + В) = Р(А) + Р(В) = 6/20 + 9/20 = 0,75.
Ответ: 0,75.
Условная вероятность события В (РА(В)) - вероятность события В, вычисленная при условии, что событие А уже произошло. Если А и В - независимые события, то РА(В) = Р(В), РВ(А) = Р(А).
Теорема 6.7. (Теорема умножения вероятностей). Вероятность произведения (пересечения; совместного появления) двух произвольных событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило, т.е. Р(АВ) = Р(А)РА(В) = Р(В)РВ(А).
Доказательство. Пусть п - число всех элементарных исходов испытания, т из этих исходов благоприятствуют событию А и d исходов благоприятствуют событиям А и В. Тогда, по определению вероятности события, имеем Р(А) = т/п, Р(АВ) = d/п. Найдем условную вероятность РА(В) события В при условии, что событие А наступило. Событие А наступает в т исходах, а в d исходах из них наступает событие В. Следовательно, РА(В) = d/т. Так как d/п = (т/п)( d/т), то Р(А В) = Р(А) РА(В). Аналогично можно показать, что Р(АВ) = Р(В) РВ(А). Теорема доказана.
Пример 6.11. На полке стоят 11 научно-популярных книг и 5 художественных. Какова вероятность того, что две подряд наугад взятые книги окажутся художественными?
Решение. Рассмотрим два события В₁ и В2: В₁ - при первом испытании взята художественная книга, Вг - при втором испытании взята художественная книга. По теореме 6.7 вероятность такого события равна Р(В1В2) = Р(В₁) РВ₁ (В2). Вероятность события В1РВ₁= 5/16. После первого испытания на полке останется 15 книг, из которых 4 художественные, поэтому условная вероятность РВ₁ (В2) = 4/15.
Отсюда искомая вероятность равна: Р(В₁Вг) =5/16∙4/15 =1/12. .
Ответ: 1/12.
Следствие 1. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляют при условии, что все предыдущие события уже наступили, т.е.
Р(А₁∙А2∙...∙Ап)= Р( А₁)• Р А₁(А2) • Р А₁ А2(А₃)•… • РА₁ РА2… РАn-1 (Ап,) .
Пример 6.12. Из десяти карточек составлено слово "МАТЕМАТИКА". Из них школьник наудачу выбирает поочередно четыре карточки и приставляет одну к другой. Какова вероятность того, что получится слово "ТЕМА"?
Решение. Введем события А₁, А2, А₃, А₄, состоящие в том, что первая выбранная буква - Т, вторая - Е, третья – М и четвертая - А. Нам нужно найти вероятность произведения этих событий. По следствию 1 из теоремы 6.7 имеем:
Р(А₁∙А2 ∙А₃∙А₄ = 2/10∙1/9∙2/8∙3/7 = 1/420.
Ответ: 1/420.
Следствие 2. Если А₁, А2, . . ., Ап - независимые события, то вероятность их произведения (совместного появления) равна произведению вероятностей этих событий, т.е. Р(А₁∙А2∙...∙Ап)= Р( А₁)• Р (А2) • …• Р(Ап).
Пример 6.13.Два стрелка независимо один от другого делают по одному выстрелу по одной и той же мишени. Вероятность поражения мишени первым стрелком - 0,7; вторым - 0,8. Какова вероятность того, что мишень будет поражена?
Решение. Пусть событие А состоит в том, что мишень поразил первый стрелок, а событие В - в том, что мишень поразил второй стрелок. По условию Р(А) = 0,7 и Р(В) = 0,8.
1-й способ. Рассмотрим противоположные события: Ᾱ - промах первого стрелка, - промах второго. По следствию 3 из теоремы 6.6 получаем Р(Ᾱ ) = 1 - 0,7 = 0,3 и Р() = 1 - 0,8 = 0,2. Произведение событий Ᾱ • означает промах обоих стрелков. По смыслу задачи события А и В являются независимыми, поэтому и противоположные события Ᾱ и также будут независимыми. По следствию 2 из теоремы 6.7 получаем вероятность того, что оба стрелка промахнутся:
Р(Ᾱ • ) = 0,3•0,2 = 0,06. Нас же интересует вероятность противоположного события, состоящего в том, что мишень поражена. Поэтому искомую вероятность мы находим по следствию 3 из теоремы 6.6: 1 - 0,06 = 0,94.
2-й способ. Искомое событие (мишень будет поражена хотя бы одним стрелком) есть сумма событий А и В. По теореме 6.6 Р(А + В) = Р(А) + Р(В) - Р(АВ) = 0,7 + 0,8 - 0,7•0,8= 1,5-0,56 = 0,94.
Ответ: 0,94.
Пример 6.14. В студенческой группе 25 человек. Какова вероятность того, что дни рождения хотя бы у двоих совпадают?
Решение. Вероятность того, что дни рождения у двух произвольно взятых людей совпадают, равна 1/365 (считаем, что попадания дня рождения на любой день в году -равновозможные случаи). Тогда вероятность того, что дни рождения двух людей не совпадают, т.е. вероятность противоположного события равна 1 - 1/365 = 364/365. Вероятность того, что день рождения третьего отличается от дней рождения двух предыдущих, составит 363/365 (363 случая из 365 благоприятствуют этому событию). Рассуждая аналогично, находим, что для 25-го члена группы эта вероятность равна 341/365. Далее найдем вероятность того, что дни рождения всех 25 членов группы не совпадают. Поскольку все эти события (несовпадение дня рождения каждого очередного члена группы с днями рождения предыдущих) независимы, то по следствию 2 из теоремы 6.7 получаем:
Р(А₁∙А2∙...∙А₂₅) = 364/365∙ 363/365∙ …∙341/365 = 0,43
Это вероятность того, что дни рождения у всех 25 человек не совпадают. Вероятность противоположного события будет вероятностью того, что хотя бы у двоих дни рождения совпадают, т.е. искомой вероятностью Р = 1 - 0,43 = 0,57.
Ответ: 0,57.
СХЕМА БЕРНУЛЛИ. Пусть А - случайное событие по отношению к некоторому испытанию. Будем считать, что испытание имеет два исхода: наступление события А и ненаступление события А (т.е. наступление события Ᾱ ). Если производится несколько таких испытаний, причем вероятность события А в каждом из них не зависит от исходов остальных, то такие испытания называют независимыми (относительно события А).
Говорят, что проводимый эксперимент удовлетворяет схеме Бернулли, если:
1) эксперимент состоит из n независимых испытаний;
2) каждое испытание имеет два исхода - наступление некоторого события А
и наступление события А;
3) вероятность события А в каждом испытании постоянна.
Теорема 6.10. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р, а не появления - q. Тогда вероятность Рп(k) того, что в n испытаниях событие А появится ровно k раз, вычисляется по формуле Бернулли: Рп(k) = С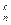 
• р 
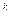q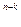 
.
 | |
Наивероятнейшее число наступления события А в n испытаниях - число k = k₀ при котором вероятность Рп(k)является наибольшей.
Теорема 6.11. Если р ≠ 0 и р ≠1,то наивероятнейшее число k₀ можно определить из двойного неравенства: n р - q£k₀ £n р + р. Если n р + р не является целым числом, то данное неравенство определяет лишь одно наивероятнейшее число. Если n р + р - целое число, то имеются два наивероятнейших значения: k₀' = n р - q и k₀'' = n р + р.Доказательство этой теоремы опускается.
Пример 6.17. Вероятность попадания в мишень при выстреле равна 0,8. Найдите:
а) вероятность того, что при семи выстрелах произойдет пять попаданий в мишень;
б) наивероятнейшее число k₀ попаданий в мишень при семи выстрелах.
Решение. Рассматриваемый в задаче эксперимент удовлетворяет схеме Бернулли. Пусть А - событие "Попадание в мишень при выстреле". Тогда событие Ᾱ означает "промах". По условию Р(А) = р = 0,8, значит, Р(Ᾱ ) = q = 1 - р = 0,2.
а) Для нахождения пяти попаданий при семи выстрелах воспользуемся теоремой 6.10: Р₇ (5) = С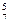 
• р 
• q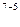 
= 7! / (5!(7-5)!• 0,8⁵• 0,2² = 0,275.
б) Наивероятнейшее число попаданий в мишень при семи выстрелах находим (согласно теоремы 6.11) из двойного неравенства 7•0,8 - 0,2 £k₀ £7 •0,8 + 0,8, т.е 5,4 £k₀ £6,4.
Значит, k₀ = 6.
Ответ: а) 0,275; б) 6.
Дата добавления: 2016-05-11; просмотров: 1764;