Лекция 14. Алгоритмы и их свойства
План:
1. Понятие алгоритма
2. Виды алгоритмов
3. Приемы построения алгоритмов
4. Основные выводы
Алгоритмы и их свойства
Большинство действий, совершаемых человеком, выполняются по определенным правилам. Их эффективность во многом зависит от того, насколько он представляет, что делать в каждый момент времени, в какой последовательности, каким должен быть итог его действий. Другими словами, результат деятельности человека непосредственно зависит от того, насколько он представляет алгоритмическую сущность своих действий.
Кроме того, применение в производстве и быту различных автоматов, компьютеров требует от человека строгого соблюдения определенной последовательности действий при их использовании, что, в свою очередь, невозможно без предварительного составления алгоритмов.
Таким образом, осмысление и разработка алгоритмов выполняемых действий становится существенным компонентом деятельности человека, составной частью его культуры мышления и поведения. Алгоритм – одно из фундаментальных понятий, которое используется в различных областях знания, но изучается оно в математике и информатике. Его освоение начинается уже в начальной школе на уроках математики, где ученики овладевают алгоритмами арифметических действий, знакомятся с правилами вычитания числа из суммы, суммы из числа и др.
Вообще формирование алгоритмического мышления у младших школьников в настоящее время является одной из важнейших задач учителя, и поэтому ему требуются определенные знания об алгоритмах, а также некоторые умения в их построении.
Понятие алгоритма
Происхождение термина «алгоритм» связано с математикой. История его возникновения такова. В IХ веке в Багдаде жил ученый ал(аль)-Хорезми (полное имя Мухаммед Бен Мусса ал-Хорезми, т.е. Мухаммед сын Мусы из Хорезма), математик, астроном, географ. В одном из своих трудов он описал десятичную систему счисления и впервые сформулировал правила выполнения арифметических действий над целыми числами и обыкновенными дробями. Арабский оригинал этой книги был утерян, но остался латинский перевод ХII в., по которому Западная Европа ознакомилась с десятичной системой счисления и правилами выполнения арифметических действий.
Ал-Хорезми стремился к тому, чтобы сформулированные им правила были понятными. Достичь этого в IХ в., когда еще не была разработана математическая символика (знаки операций, скобки, буквенные обозначения и т.д.), было трудно. Однако ему удалось выработать четкий стиль строгого словесного предписания, который не давал читателю возможность уклониться от предписанного или пропустить какие-нибудь действия.
Правила в книгах ал-Хорезми в латинском переводе начинались словами «Алгоризми сказал». В других латинских переводах автор именовался как Алгоритмус. Со временем было забыто, что Алгоризми (Алгоритмус) – это автор правил, и эти правила стали называть алгоритмами. Многие столетия разрабатывались алгоритмы для решения все новых и новых классов задач, но само понятие алгоритма не имело точного математического определения.
В настоящее время понятие алгоритма уточнено, и сделано это в ХХ веке в рамках науки, называемой теорией алгоритмов.
Будем рассматривать алгоритм как программу действий для решения задач определенного типа.
Чтобы какую-либо программу действий можно было назвать алгоритмом, она должна удовлетворять ряду требований. Эти требования называют свойствами алгоритма.
1. Каждая программа, задающая алгоритм, должна состоять из конечного числа шагов, а каждый шаг должен быть точно и однозначно определен. Это свойство алгоритмов называется свойством определенности (или детерминированности).
Согласно этому свойству в алгоритмах не может быть таких, например, предписаний, как «сложить х с одним из данных чисел а или b», «привести два-три примера истинных и ложных высказываний» и т.д.
2. Шаги в алгоритме должны идти в определенной последовательности. Это означает, что в любом алгоритме для каждого шага (кроме последнего) можно указать единственный непосредственно следующий за ним шаг, т.е. такой, что между ними нет других шагов. Это свойство дискретности алгоритмов.
Дискретная структура алгоритмов хорошо вида в алгоритмах выполнения арифметических действий. Например, алгоритм нахождения суммы чисел 34 + 23 формулируется так:
1) Пишу десятки под десятками, а единицы под единицами.
2) Складываю единицы: 4 + 3 = 7, пишу 7 под единицами.
3) Складываю десятки: 3 + 2 = 5, пишу 5 под десятками.
4) Читаю ответ: сумма равна 57.
3. Каждый шаг программы, задающей алгоритм, должен состоять из выполнимых действий. Это означает, что предусмотренные действия были выполнимы теми исполнителями, которым она адресована. Так, например, задание «решить уравнение х + 9 = 17» один ученик уверенно выполняет и получает искомое значение переменной х, так как владеет всеми действиями, необходимыми для решения простейших уравнений.
1) прочитай уравнение;
2) вспомни правило, как найти значение неизвестного;
3) реши уравнение;
4) сделай проверку;
5) запиши ответ.
Другой не справляется с заданием или получает неверный ответ, так как не владеет хотя бы одним из действий, которые требуются для выполнения данного задания.
Как видно из примера, под словом «действие» понимаются не только математические операции, но оно имеет и более широкий смысл.
Кроме того, в алгоритмах недопустимы также ситуации, когда после выполнения очередного действия исполнителю неясно, какое из них должно выполняться на следующем этапе.
Все сказанное характеризует свойство алгоритма, называемое свойством понятности.
4. Программа, задающая алгоритм, должна быть направлена на получение определенного результата. Получение результата за конечное число шагов составляет свойство результативности алгоритма.
5. Программа, задающая алгоритм, должна быть применима к любой задаче рассматриваемого типа. Другими словами, каждый алгоритм решения линейного уравнения первой степени применяется для решения всех уравнений вида ах + b = 0. В этом состоит свойство массовости алгоритма.
Задачи, для которых может быть составлен алгоритм, и в результате выполнения этого алгоритма получен ответ на вопрос (даже если ответ, что задача не имеет решения), называются алгоритмически разрешимыми.
Алгоритмы могут предназначаться как исполнителю-человеку, так и исполнителю-машине. И в связи с этим между ними могут быть различия. Действия, понятные человеку, могут быть не понятны машине (например, действие «вспомни правило»), и наоборот. Предписания для человека могут содержать желательные, но не обязательные действия, или их можно поменять местами. Например, чтобы определить значение истинности конъюнкции двух высказываний А и В, нужно:
1) определить значение истинности высказывания А;
2) определить значение истинности высказывания В;
3) определить значение истинности высказывания А ∧ В.
Так как операция конъюнкции коммутативна, т.е. А ∧ В ⇔ В ∧ А, то пункты 1) и 2) можно поменять местами. Такой выбор последовательности шагов осуществляет исполнитель-человек, но не машина. Если свойства детерминированности и дискретности сохраняются с некоторой степенью точности, т.е. в программе возможна перестановка шагов или она содержит желательные, но не обязательные шаги, то мы имеем не алгоритм, а алгоритмическое предписание. Однако, несмотря на различия между этими понятиями, часто алгоритмические предписания называются алгоритмами.
Известны различные способы записи алгоритмов: словесная запись, формульная, табличная, на языке блок-схем или алгоритмическом языке.
Словесная запись –это форма представления алгоритмических предписаний. Она допускает употребление естественного языка и математической символики, что делает предписание понятным и доступным для усвоения. Форму словесной записи имеют многие «бытовые» алгоритмические предписания, часто применяемые в повседневной жизни: как испечь пирог, как пользоваться электроприбором, как получить книгу в библиотеке и т.д. Вообще в этой форме могут быть описаны любые предписания, в том числе и математические. Например, алгоритмическое предписание нахождения середины отрезка АВ может иметь вид:
1) поставить ножку циркуля в точку А;
2) установить раствор циркуля в точку А;
3) провести окружность;
4) поставить ножку циркуля в точку В;
5) провести окружность;
6) отметить точки пересечения окружностей;
7) через отмеченные точки провести прямую;
8) отметить точку пересечения прямой с отрезком АВ.
Алгоритмы, используемые для вычислений, могут быть записаны в формульной (т.е. с помощью формулы) или табличной (т.е. с помощью таблицы) формах. Например, для нахождения корней квадратного уравнения ах2 + bх + с = 0 (а ¹ 0) удобнее применять не словесную запись, а формулу:
х = (- b ± √ b - 4ac) : 2a
Запись алгоритма, используемого для вычислений, в форме таблицы удобно использовать, когда требуется найти не одно, а несколько значений одного и того же выражения для различных значений переменных, входящих в данное выражение.
Рассмотрим алгоритмическое предписание решения следующей задачи: «В одном куске 72 м ткани, а в другом в у раз больше. Сколько метров ткани во втором куске? Составь выражение и найди его значение, если у = 2, 4, 8».
Словесная запись алгоритма решения данной задачи такова:
1) составить выражение;
2) найти его значение для у = 2;
3) найти его значение для у = 4;
4) найти его значение для у = 8.
Если же оформить предписание в виде таблицы, то запись будет иметь вид:
| Значение переменной | у | 2 | ||
| Значение выражения | 72 - у |
Алгоритмы можно записывать на языке блок-схем. Такое их представление, состоящее из блоков и стрелок, выполняется следующим образом:
1) каждый шаг записывается в форме определенной геометрической фигуры (блока);
2) блок, соответствующий команде, предусматривающей выполнение некоторого действия, в результате которого образуется какой-то новый промежуточный или конечный результат, изображается в виде прямоугольника. Внутри него записывается выполняемое действие.
Такие блоки называются арифметическими, или, в более общем виде, перерабатывающими информацию, так как не всегда выполняемые действия являются арифметическими;
3) блок, соответствующий команде, предусматривающей проверку некоторого условия, изображается в виде ромба. Проверяемое логическое условие записывается внутри него. Выполнение данной команды не приводит к новому результату, а лишь определяет дальнейший ход процесса решения. Такие блоки называются логическими;
4) если за шагом А непосредственно следует шаг В, то от блока А к блоку В проводится стрелка. От каждого арифметического блока исходит только одна стрелка; от каждого логического - две стрелки: одна с пометкой «да» (или «+»), идущая к блоку, следующему за логическим
блоком, если условие выполняется, другая - с пометкой «нет» (или «-»), идущая к блоку, следующему за логическим, если условие не выполняется;
5) начало и конец алгоритма изображаются блоками в виде овалов, внутри которых записываются соответственно слова «Начало» и «Конец».
|
| х + 24 |
|
| да |
В качестве примера такой записи рассмотрим алгоритмическое предписание для решения задачи: «Из ряда чисел 15, 16, 17, 18 выпиши значения х при которых верно неравенство .у + 24 > 40
| нет |
| х выписать |

Рис 61.
В соответствии с этой схемой устанавливаем, что если х = 15, то х + 24 не больше 40, следовательно, при этом значении х неравенство х + 24 > 40 верным не будет. Аналогично для х = 16. Если же х = 17, то х + 24 будет больше 40, и, значит, при этом значении х неравенство х + 24 > 40 будет верным. Аналогично и для х = 18.
Видим, что блок-схема наглядно представляет логику решения задачи. Поэтому запись алгоритмов в виде блок-схем имеет широкое распространение.
Еще один способ - это запись на определенном алгоритмическом языке. Она используется в том случае, когда исполнитель данного алгоритма - машина, причем каждая машина имеет свой, только ей понятный язык: фортран, паскаль, бейсик, лого и др.
В зависимости от порядка выполнения действий различают следующие виды алгоритмических процессов: линейные, разветвляющиеся, циклические.
|
| Числа Кончились Да |
Если в алгоритме действия выполняются последовательно друг за другом, то он называется линейным. Если в алгоритме порядок действий зависит от некоторого условия, он называется разветвляющимся. Если в алгоритме некоторые действия могут выполняться многократно, то он называется циклическим.
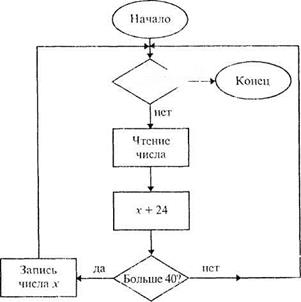
Рис. 62
Примером линейного алгоритмического предписания является ранее рассмотренное нами предписание нахождения середины отрезка. На рисунке 61 в виде блок-схемы представлен разветвляющийся алгоритм выбора из данных чисел тех, которые удовлетворяют неравенству х + 24 > 40. Так как в этом алгоритмическом предписании последовательность действий должна повториться для каждого из данных чисел, то его можно сделать циклическим. Для организации цикла необходимо осуществить перебор всех значений и предусмотреть выход из цикла (рис. 62).
Упражнения
1. Установите, для решения каких задач используются следующие
алгоритмы:
А л г о р и т м А.
1) Пишу единицы под единицами, десятки под десятками, сотни под сотнями.
2) Складываю единицы: 4 + 2 = 6.
3) Складываю десятки: 6 + 4 = 10, десять десятков равны одной сотне. Пишу под десятками 0, а одну сотню запомню и прибавлю к сотням.
4) Складываю сотни: 2 + Я = 7, да еще 1, получится 8. Пишу 8 под сотнями.
5) Читаю ответ: 806.
А л г о р и т м Б.
1) Отметь на листе бумаги точку О.
2) Установи раствор циркуля равным длине отрезка АВ.
3) Поставь ножку циркуля в точку О.
4) Проведи окружность.
2. Объясните, почему следующая программа действий является алгоритмическим предписаннем:
Собери портфель
1) Открой портфель.
2) Положи в портфель тетради.
3) Положи в портфель учебники.
4) Положи в портфель карандаш.
5) Положи в портфель ручку.
6) Закрой портфель,
3. Является ли следующая программа действий алгоритмом или
алгоритмическим предписанием
А. Измерение длины отрезка АВ.
1) Совместить линейку с отрезком АВ, совместив О с А.
2) Отметить число, соответствующее точке В.
3) Записать полученное значение.
Б. Построение биссектрисы угла (рис.63).

Рис.63
1) Провести циркулем дугу окружности, пересекающую стороны данного угла, и с центром в вершине угла.
2) Обозначить точки пересечения душ окружности со сторонами угла буквами А и В
3) Провести окружность с центром в точке А и тем же радиусом.
4) Провести окружность с центром в точке В и тем же радиусом.
5) Обозначить одну из точек пересечения окружностей буквой С.
6) Провести луч из вершины угла через точку С.
4. Составьте алгоритм вычисления по формуле:
а) у = (5х -3) × (2х + 7);
б) у = 2× (х + 8)-1.
5. По приведенному алгоритму восстановите формулу для вычисления значения у:
1) Умножить х на 4, обозначить результат R₁.
2) Сложить R₁, с числом 7, обозначить результат R₂.
3) Разделить R₂на х, считать результат значением у.
6. Алгоритм получения кипятка задан при помощи блок-схемы
Какой вид будет иметь блок-схема этого алгоритма при условии, что:
а) в чайнике уже есть вода;
б) плита включена?
7. Составьте алгоритм вычисления в миллиметрах длины ломаной, состоящей из:
а) двух звеньев; 6) пяти звеньев.
8. Составьте алгоритм построения отрезка длиной 5 см. Какие изменения произойдут в нем с изменением длины отрезка?
9.Составьте и запишите алгоритм построения на клетчатой бумаге квадрата со стороной
5 см. Какие изменения надо внести в него, чтобы построить квадрат: а) со стороной 5 см на нелинованной бумаге; б) со стороной любой длины?
Дата добавления: 2016-05-11; просмотров: 4044;
