Измерение вариации по уравнению регрессии.
Для проверки того, насколько хорошо независимая переменная предсказывает зависимую переменную в полученной регрессионной модели, необходим расчет ряда мер вариации. Первая из них - общая (полная) сумма квадратов отклонений результативного признака от средней - есть мера вариации значений Yi относительно их среднего 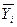 . В регрессионном анализе общая сумма квадратов может быть разложена на объясняемую вариацию или сумму квадратов отклонений за счет регрессии и необъясняемую вариацию или остаточную сумму квадратов отклонений (рис. ).
. В регрессионном анализе общая сумма квадратов может быть разложена на объясняемую вариацию или сумму квадратов отклонений за счет регрессии и необъясняемую вариацию или остаточную сумму квадратов отклонений (рис. ).
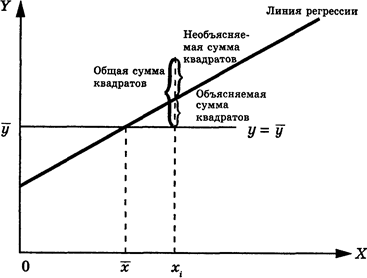
Рисунок - Графическая интерпретация вариации по уравнению регрессии .
Сумма квадратов отклонений вследствие регрессии это сумма квадратов разностей между 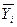 (средним значениемY) и Y xi (значением Y, предсказанным по уравнению регрессии).
(средним значениемY) и Y xi (значением Y, предсказанным по уравнению регрессии).
Сумма квадратов отклонений, не объясняемая регрессией (остаточная сумма квадратов), это сумма квадратов разностей Yi и Y xi . Эти меры вариации могут быть представлены следующим образом (табл.5):
Таблица 5
| Общая сумма квадратов (ST) | = | Сумма квадратов за счет регрессии (SR) | + | Остаточная сумма квадратов (SE) |
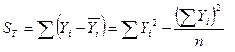 (25)
(25)
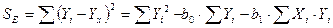 ( 26 )
( 26 )
( 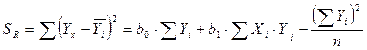 27 )
27 )
Остаточная сумма квадратов SЕ 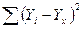 - это выражение, стоящее под знаком корня в формуле стандартной ошибки оценки. Тем не менее, в процессе вычислений стандартной ошибки мы всегда вначале вычисляем сумму квадратов ошибки.
- это выражение, стоящее под знаком корня в формуле стандартной ошибки оценки. Тем не менее, в процессе вычислений стандартной ошибки мы всегда вначале вычисляем сумму квадратов ошибки.
Остаточная сумма квадратов может быть представлена следующим образом:
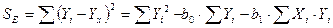 =1602,0971-2,423 ·176,11-0,00873 134127,90= 4,446;
=1602,0971-2,423 ·176,11-0,00873 134127,90= 4,446;
Объясняемая сумма квадратов выразится так:
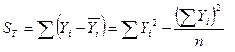 = = 1602,0971 -1550,7366 51,3605.
= = 1602,0971 -1550,7366 51,3605.
SR = 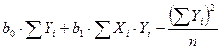
 =2,423 •176,11-0,00873 ·134127,90=46,9145.
=2,423 •176,11-0,00873 ·134127,90=46,9145.
В самом деле
51,3605 = 46,9145 + 4,4460.
Из этого соотношения определяется коэффициент детерминации:
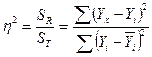
 (28)
(28)
Таким образом, коэффициент детерминации - доля вариации Yi, которая объясняется независимыми переменными в регрессионной модели. Для нашего примера η2 = 46,9145/51,3605 = 0,913.
Следовательно, 91,3% вариации уровня рентабельности могут быть объяснены средней выработкой на одного работника, варьирующим от предприятия к предприятию.
Только 8,7% вариации можно объяснить иными факторами, не включенными в уравнение регрессии. В случае парной регрессии коэффициент детерминации равен квадратному корню из квадрата коэффициента линейной корреляции Пирсона.
В простой линейной регрессии г имеет тот же знак, что и b1. Если b1> 0, то г > 0; если b1< 0, то г < 0, если b1= 0, то г == 0.
В рассматриваемом примере η2 = 0,913 и b1> 0, коэффициент корреляции
г = 0,955. Близость коэффициента корреляции к 1 свидетельствует о тесной положительной связи между уровнем рентабельности предприятия и величиной средней выработки на одного работника. Так как η = 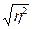 =0,956 (η>r), то это очень незначительное расхождение свидетельствует о том, что рассматриваемый экономический процесс можно аппроксимировать линейной зависимостью.
=0,956 (η>r), то это очень незначительное расхождение свидетельствует о том, что рассматриваемый экономический процесс можно аппроксимировать линейной зависимостью.
Мы интерпретировали коэффициент корреляции в терминах регрессии, однако корреляция и регрессия - две различные техники. Корреляция устанавливает силу связи между признаками, а регрессия — форму этой связи.
Дата добавления: 2016-11-02; просмотров: 891;
