Стандартная ошибка оценки уравнения регрессии

Хотя метод наименьших квадратов дает линию регрессии, которая обеспечивает минимум вариации, регрессионное уравнение не является идеальным в смысле предсказания, поскольку не все значения зависимого признака Y удовлетворяют уравнению регрессии. Необходима статистическая мера вариации фактических значений Y от предсказанных значений Y. Эта мера в то же время является средней вариацией каждого значения относительно среднего значения Y.

Мера вариации относительно линии регрессии называется стандартной ошибкой оценки.

Колеблемость фактических значений признака Y относительно линии регрессии может быть показана как совокупность точек, расположенных выше или ниже теоретической линии регрессии.

Стандартная ошибка оценки S_yx определяется как:

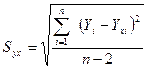, (24)

где Y _i – фактические значения Y; Y _xi - теоретические значения X по уравнению регрессии.

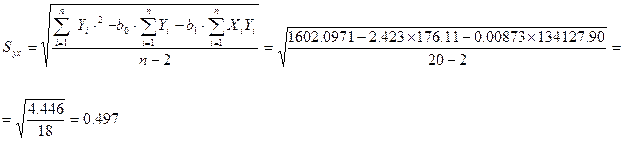
Для рассматриваемого примера: S_yx=0,497. Эта стандартная ошибка характеризует меру вариации фактических данных относительно линии регрессии. Интерпретация этой меры аналогична интерпретации среднего квадратического отклонения. Если среднее квадратическое отклонение — это мера вариации относительно средней, то стандартная ошибка - это оценка меры вариации относительно линии регрессии. Однако стандартная ошибка оценки может быть использована для выводов о значении Y_x, и выяснения, является ли статистически значимой взаимосвязь между двумя переменными.