Структура ряда динамики. Проверка ряда на наличие тренда
Всякий ряд динамики теоретически может быть представлен в виде составляющих:
1) тренд - основная тенденция развития динамического ряда (к увеличению либо снижению его уровней);
2) циклические (периодические) колебания, в том числе сезонные;
3) случайные колебания.
Изучение тренда включает два основных этапа:
1) ряд динамики проверяется на наличие тренда;
2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Проверка на наличие тренда в ряду динамики может быть осуществлена по нескольким критериям.
1 . Метод средних.
Изучаемый ряд динамики разбивается на несколько интервалов (обычно на два), для каждого из которых определяется средняя величина (У, У). Выдвигается гипотеза о существенном различии средних. Если эта гипотеза принимается, то признается наличие тренда.
2. Фазочастотный критерий знаков первой разности (Валлиса и Мура).
Суть его заключается в следующем: наличие тренда в динамическом ряду утверждается в том случае, если этот ряд не содержит либо содержит в приемлемом количестве фазы - изменение знака разности первого порядка (абсолютного цепного прироста).
3. Критерий Кокса и Стюарта.
Весь анализируемый ряд динамики разбивают на три равные по числу уровней группы (в том случае, если количество уровней ряда динамики не делится на три, недостающие уровни нужно добавить) и сравнивают между собой уровни первой и последней групп.
4. Метод серий.
По этому способу каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов: например, если уровень ряда меньше медианного значения, то считается, что он имеет тип А, в противном случае - тип В.
В образовавшейся последовательности типов определяется число серий. Серией называется любая последовательность элементов одинакового типа, граничащая с элементами другого типа.
Так как имеющиеся данные могут иметь различные функции распределения, то целесообразно принимать решение о наличии тренда на основе использования свободных от распределений или непараметрических методов, в которых относительно функции распределения полученных данных не делается никаких предположений. Или же данных настолько мало, что корректно проверить гипотезу о наличии конкретного распределения невозможно. Наиболее известными не зависящих от формы распределения методами, которые применяются для оценки наличия тренда в совокупности данных, являются: критерий серий и критерий инверсий.
Критерий серий
Рассмотрим последовательность N значений случайной величины x(k) и каждое значение отнесем к одной из двух взаимно исключающих категорий, которые обозначим знаками плюс (+) и минус (-). В качестве примера рассмотрим последовательность измеренных значений величины xi при i = 1, 2, 3, ..., N, среднее значение которых равно 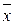 . Каждое наблюденное значение
. Каждое наблюденное значение
xi ³ 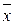 обозначим (+), а если xi <
обозначим (+), а если xi < 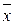 , то (-).
, то (-).
Полученная последовательность наблюдений, имеющих знак плюс или минус, может выглядеть следующим образом:
+ + - + + - + + + - + - - + - - + - - -
1 2 3 4 5 6 7 8 9 10 11 12
Серией называется последовательность одинаковых значений, перед которыми или после которых расположены значения другой категории или наблюдения отсутствуют вообще.
В рассмотренном примере имеется r = 12 серий в последовательности из N = 20 наблюдений.
Число серий, которое встречается в последовательности наблюдений, позволяет определить, являются ли результаты независимыми случайными наблюдениями над одной и той же случайной величиной. Если после-довательность N наблюдений представляет собой независимые наблюденные значения одной и той же случайной величины, т. е. вероятность знаков (+) и (-) не меняется от одного наблюдения к другому, то выборочное распределение числа серий в последовательности есть случайная величина r(k) со средним значением
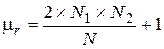
и дисперсией
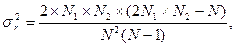
где N1 - число наблюдений со знаком (+), N2 - число наблюдений со знаком (-). В частном случае, когда N1 = N2 =N/2 , представленные соотношения перепишутся в виде
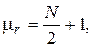
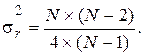
В приложении 1 приведена таблица, содержащая данные о 100a-про-центных точках функции распределения r(k).
Если последовательность значений содержит тренд, то это означает, что вероятность знаков (+) или (-) меняется от одного наблюденного значения к другому. Наличие тренда можно проверить следующим образом. Рассмотрим гипотезу об отсутствии тренда, т. е. предположим, что полученные данные представляет собой независимые значения одной и той же случайной величины. Полагая, что число наблюденных значений со знаком (+) равно числу значений со знаком (-), можно считать, что число серий в последовательности будет иметь выборочное распределение, представленное в приложении 1. Гипотезу можно подвергнуть проверке при любом уровне значимости a путем сопоставления фактического числа серий с граничными значениями rn; 1-a/2 и rn; a/2, где n=N/2 . Если фактическое число серий выходит за границы этого интервала, гипотезу следует отвергнуть при выбранном уровне значимости. В противном случае ее можно принять.
Например, имеется последовательность из N=20 чисел: 5,5; 5,1; 5,7; 5,2; 4,8; 5,7; 5,0; 6,5; 5,4; 5,8; 6,8; 6,6; 4,9; 5,4; 5,9; 5,4; 6,8; 5,8; 6,9; 5,5.
Определим, являются ли независимыми наблюденные значения, путем проверки числа серий, которые встречаются, если отсчитывать наблюденные значения от их медианы. Выполним проверку при уровне значимости a = 0,05.
Просматривая выборку, можно убедиться, что медианой данного ряда является значение x = 5,6. Примем, что числа более 5,6 имеют знак (+), а менее 5,6 - знак (-). В результате получаем последовательность
- - + - - + - + - + + + - - + - + + + -
1 2 3 4 5 6 7 8 9 10 11 12 13
Таким образом, имеется 13 серий, представляющих последовательность 20 наблюденных значений.
Рассмотрим гипотезу о независимости наблюденных значений. Область принятия этой гипотезы определяется интервалом [r10; 1-a/2 < r £ r10; a/2].
По данным приложения 1 при a = 0,05 находим r10; 1-a/2 = r10; 0,975 = 6 и
r10; a/2 = r10; 0,025 = 15. Нулевая гипотеза принимается, так как значение r = 13 входит в интервал между 6 и 15. Другими словами нет причин подвергнуть сомнению то обстоятельство, что наблюденные значения независимы. Это значит, что нет никаких доказательств присутствия тренда.
Критерий инверсий
Рассмотрим последовательность N значений случайной величины x(k). Обозначим эти значения символом xi, где i == 1, 2, 3, ..., N.
Подсчитаем теперь число случаев, когда xi > xj, при i<j. Каждое такое неравенство называется инверсией. Общее число инверсий обозначается символом А, которое формально определяется так.
По ряду значений x1, x2 …, xN определим величину
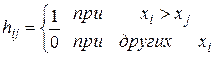 .
.
Тогда 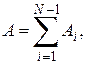 где
где 
Например,
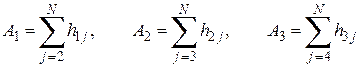 и т.д.
и т.д.
Для примера рассмотрим последовательность N = 8 значений: x1=5, x2=3, x3=8, x4=9, x5=4, x6=1, x7=7, x8=5. В этой последовательности x1 > x2, x1 > x5 и
x1 > x6, откуда находим А1 = 3 инверсиям для x1. Сопоставляя значение x2 с последующими значениями ряда (т. е. при i = 2 и i < j = 3, 4,..., 8), можно найти, что x2 > x6 и только. Поэтому число инверсий для x2 составляет A2 = 1. Продолжая анализ, можно видеть, что A3 = 4, A4 = 4, A5 = 1, A6 = 0, A7 = 1. Общее число инверсий составит A = A1 + A2 + … + A7 = 3+1+4+4+1+0+1 = 14 .
Если последовательность N наблюдений содержит независимые значения одной и той же случайной величины, то число инверсий есть случайная величина А(k) со средним значением
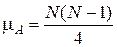
и дисперсией
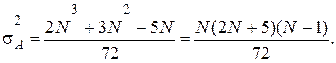
В приложении 2 содержатся данные о 100a-процентных точках функции распределения величины А(k).
Критерий инверсий вообще говоря, имеет большую мощность, чем критерий серий, при выявлении монотонного тренда в последовательности наблюдений. Однако критерий инверсий обладает малой мощностью при выявлении колебательного тренда.
Например, проверим последовательность N = 20 значений, рассмотренных ранее, на наличие тренда при уровне значимости a = 0,05. Число инверсий в этом случае таково:
| А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | А11 | А12 | А13 | А14 | А15 | А16 | А17 | А18 | А19 |
Общее число инверсий А= 62.
Рассмотрим гипотезу о том, что наблюдения представляют независимые значения случайной величины х(k), не содержащей тренда. Область принятия гипотезы определяется неравенством A20; 1-a/2 < A £ A20; a/2. По данным приложения 2 при a = 0,05 находим A20;1-a/2=A20;0,975 = 64 и A20;a/2=A20;0,025= 125.
Следовательно, гипотезу отвергают при 5%-ном уровне значимости, так как значение А = 62 не попадает в интервал между 64 и 125.
Заметим, что гипотеза о независимости этой же последовательности значений при использовании критерия серий была принята. Этот факт иллюстрирует разницу в чувствительности двух методов проверки.
Таблица 11 – Таблица исходных данных и расчетных показателей динамического ряда
(изменения стоимости зернокомбайна «Дон 1500» во времени)
| Время T | Цена Р, руб | D баз= Yi-Yo | D цеп= Yi -Yi-1 | Кр баз =Yi/Yo | Tр баз= 100*Yi/Yo | Кр цеп= Yi/Yi-1 | Tр цеп= 100*Yi/Yi-1 | Кпр.баз= Кр.баз-1 | Tпр баз= 100*Кр. цеп | Кпр цеп= Кр цеп-1 | Тпр цеп= Кпр цеп*100 | А цеп= Yi-1/100 |
| 1995 1п/г | - | - | 0,66 | 66,34 | -0,337 | -33,659 | - | |||||
| 1995 2п/г | -95260 | 0,75 | 74,72 | 1,13 | 112,63 | -0,25 | -25,28 | 0,13 | 12,63 | |||
| 1996 1п/г | -25030 | 0,93 | 93,36 | 1,25 | 124,94 | -0,07 | -6,64 | 0,25 | 24,94 | 2815,8 | ||
| 1996 2п/г | 1,00 | 100,00 | 1,07 | 107,11 | 0,00 | 0,00 | 0,07 | 7,11 | 3518,1 | |||
| 1997 1п/г | 1,08 | 107,74 | 1,08 | 107,74 | 0,08 | 7,74 | 0,08 | 7,74 | 3768,4 | |||
| 1997 2п/г | 1,12 | 111,72 | 1,04 | 103,70 | 0,12 | 11,72 | 0,04 | 3,70 | 4059,9 | |||
| 1998 1п/г | 1,25 | 124,72 | 1,12 | 111,64 | 0,25 | 24,72 | 0,12 | 11,64 | ||||
| 1998 2п/г | 1,41 | 140,78 | 1,13 | 112,87 | 0,41 | 40,78 | 0,13 | 12,87 | ||||
| 1999 1п/г | 1,72 | 172,49 | 1,23 | 122,53 | 0,72 | 72,49 | 0,23 | 22,53 | ||||
| 1999 2п/г | 2,23 | 223,17 | 1,29 | 129,38 | 1,23 | 123,17 | 0,29 | 29,38 | ||||
| 2000 1п/г | 2,93 | 293,00 | 1,31 | 131,29 | 1,93 | 193,00 | 0,31 | 31,29 | ||||
| 2000 2п/г | 3,50 | 350,39 | 1,20 | 119,59 | 2,50 | 250,39 | 0,20 | 19,59 | ||||
| 2001 1п/г | 4,06 | 405,74 | 1,16 | 115,80 | 3,06 | 305,74 | 0,16 | 15,80 | ||||
| 2001 2п/г | 4,78 | 477,92 | 1,18 | 117,79 | 3,78 | 377,92 | 0,18 | 17,79 |
3.5. Средние показатели рядов динамики
Средние показателирядов динамики являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста.
Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.
В интервальном ряду динамики с равноотстоящимиуровнями во времени расчет среднего уровня ряда 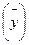 производиться по формуле средней арифметической простой:
производиться по формуле средней арифметической простой:
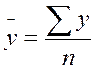 .
.
Средний уровень ряда для цены зернокомбайна по исходным данным
составляет:
Рср = 10333219/15=688881,26 руб
Если интервальный ряд динамики имеет не равноотстоящиеуровни, то средний уровень ряда вычисляется по формуле
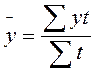 ,
,
где t – число периодов времени, в течение которых уровень не изменяется.
Для моментального ряда сравноотстоящимиуровнями средняя хронологическаярассчитывается по формуле
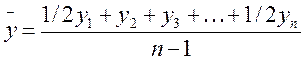 ,
,
где n – число уровней ряда.
Средняя хронологическая для неравноотстоящих уровнеймоментного ряда динамики вычисляется по формуле
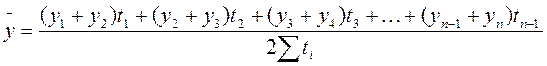 .
.
Определение среднего абсолютного прироста производится по цепным абсолютным приростам по формуле:
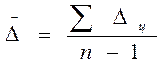 или
или 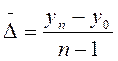 .
.
Средний абсолютный прирост для цены комбайна «Дон 1500» составляет
85322,34/14=6094,5 руб
Среднегодовой темп роста вычисляется по формуле средней геометрической:
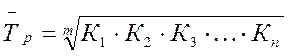 , или
, или
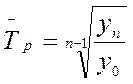 ,
,
где m – число коэффициентов роста.
Среднегодовой темп роста для зернокомбайна составляет:
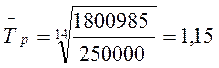
Среднегодовой темп прироста получим, вычтя из среднего темпа роста 100%.
Среднегодовой темп прироста для зернокомбайна «Дон 1500» составляет 15 %.
Дата добавления: 2016-11-02; просмотров: 1882;
