Коефіцієнт кореляції та його властивості
Означення 17.6. Коефіцієнтом кореляції випадкових величин  та
та  називається величина
називається величина
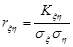 . (17.7)
. (17.7)
Розглянемо властивості коефіцієнта кореляції.
1. Коефіцієнт кореляції за абсолютною величиною не перевищує 1, тобто 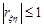 .
.
Ця властивість є наслідок властивості 6 кореляційного моменту.
2. Якщо випадкові величини незалежні, то їх коефіцієнт кореляції дорівнює 0.
Дійсно, з незалежності випадкових величин випливає, що вони некорельовані, тобто 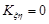 . Із означення 17.6 маємо, що
. Із означення 17.6 маємо, що 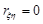 .
.
3. Некорельованими можна вважати випадкові величини, для яких 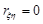 .
.
4. Якщо коефіцієнт кореляції випадкових величин дорівнює за абсолютною величиною 1, то між цими випадковим величинами існує лінійні функціональна залежність.
Доведення. Вище отримали рівність
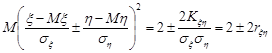 .
.
Нехай 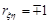 , тоді
, тоді 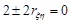 . Отже,
. Отже,
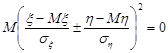 .
.
Рівність нулю математичного сподівання невід’ємної випадкової величини означає, що сама випадкова величина тотожньо дорівнює нулю, тобто
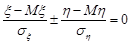 .
.
Звідси випливає, що, якщо 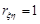 , то
, то 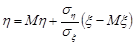 , а при
, а при 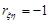 маємо
маємо 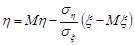 , тобто випадкові величини
, тобто випадкові величини  та
та  зв’язані лінійною функціональною залежністю.
зв’язані лінійною функціональною залежністю.
Не важко довести й обернене твердження: якщо випадкові величини  та
та  зв’язані лінійною функціональною залежністю, то
зв’язані лінійною функціональною залежністю, то 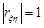 .
.
У випадку n-вимірного випадкового вектора  розглядають коефіцієнти кореляції окремих компонент
розглядають коефіцієнти кореляції окремих компонент
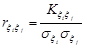 ,
, 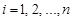 ,
, 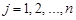 .
.
Аналогічно для n-вимірного випадкового вектора складають нормовану кореляційну матрицю
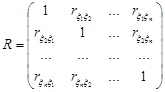 .
.
Приклад 17.4. Система дискретних випадкових величин  задана таблицею розподілу (табл. 17.2).
задана таблицею розподілу (табл. 17.2).
Таблиця 17.2

| 
| ||
| -1 | 0,10 | 0,20 | 0,15 |
| 0,25 | 0,10 | 0,20 |
Скласти кореляційну та нормовану кореляційну матриці випадкового вектора 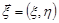 .
.
Розв’язання. Побудуємо ряди розподілу кожної компоненти:

| 
| 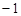
| |||||
| р | 0,35 | 0,30 | 0,35 | р | 0,45 | 0,55 |
Обчислимо перші та другі моменти випадкових величин:
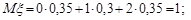
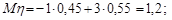
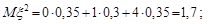
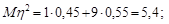
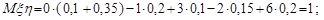
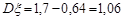 ;
; 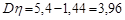 ;
;
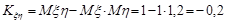 .
.
Отже, кореляційна матриця має вигляд:
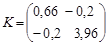 .
.
Обчислимо коефіцієнт кореляції випадкових величин  та
та  за формулою
за формулою 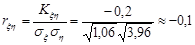 . Отже, нормована кореляційна матриця буде такою
. Отже, нормована кореляційна матриця буде такою
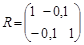 .
.
Приклад 17.5. Скласти кореляційну та нормовану кореляційну матриці випадкового вектору 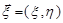 , який рівномірно розподілений в еліпсі:
, який рівномірно розподілений в еліпсі: 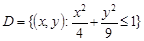 .
.
Розв’язання. Щільність розподілу рівномірно розподіленого випадкового вектору має вигляд:
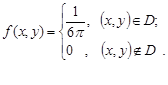
Внаслідок симетрії відносно початку координат області розподілення D математичні сподівання випадкових величин  та
та  дорівнюють нулю, тобто
дорівнюють нулю, тобто 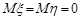 . Обчислимо дисперсії випадкових величин
. Обчислимо дисперсії випадкових величин
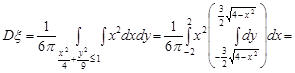
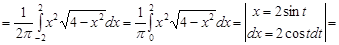
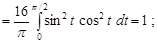
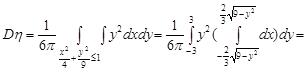
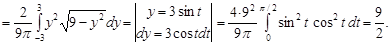
Кореляційний момент випадкових величин дорівнює
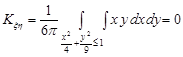 .
.
Отже, кореляційна матриця та нормована кореляційна матриця мають вигляд
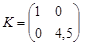 ,
, 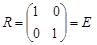 .
.
Дата добавления: 2016-11-02; просмотров: 4230;
