Кореляційний момент та його властивості. Коефіцієнт кореляції

Згідно з означенням 17.5 кореляційний момент двох випадкових величин та є величина, яка обчислюється за формулою

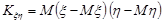. (17.4)

Для дискретних випадкових величин ця формула набуває вигляд

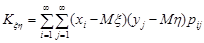, (17.5)

де .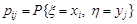

Для неперервних випадкових величин ця формула буде такою

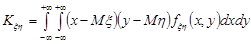. (17.6)

де 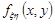– щільність розподілу випадкового вектора .

Кореляційний момент двох випадкових величин характеризує як ступінь залежності так і розсіювання випадкових величин. Це власне випливає з властивостей кореляційного моменту.

1. Має місце формула

,

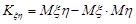яка для дискретних випадкових величин набуває вигляд

,

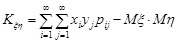а для неперервних випадкових величин

.

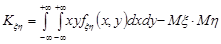Доведення. Із формули (17.4) маємо

.

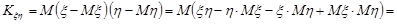
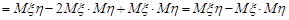2. Якщо випадкові величини та незалежні, то .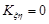

Доведення. Проведемо доведення для неперервних випадкових величин. Оскільки випадкові величини та незалежні, то 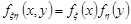, тоді

.

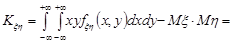
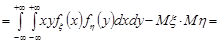
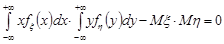3. Твердження обернене твердженню 2, взагалі кажучі, місця не має. Пояснимо на прикладі.

Приклад 17.3. Випадковий вектор 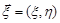є рівномірно розподіленим в області D = { 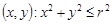}. Знайти його кореляційний момент та з’ясувати питання про незалежність випадкових величин та .

Розв’язання. За умовою задачі вектор 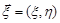– рівномірно розподілений в області D. Отже, щільність розподілу цього вектора має вигляд

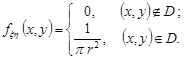
В силу симетрії області D та рівномірності розподілу випадкового вектора 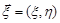математичні сподівання компонент дорівнюють нулю. Тоді неважко показати, що

.

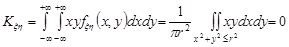Для перевірки незалежності компонент випадкового вектора 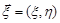знайдемо щільності розподілу цих компонент за формулами (15.4):

, .

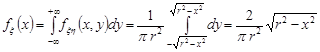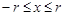Аналогічно

; .

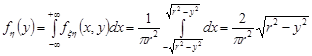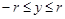Оскільки 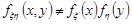, то випадкові величини та – залежні.

Введемо означення.

Означення 17.5. Випадкові величини та називаються некорельованими, якщо 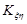= 0.

Висновок. Якщо випадкові величини та незалежні, то вони завжди некорельовані. Але з некорельованості випадкових величин ще не випливає, взагалі кажучи, їх незалежність. Виняток цього твердження буде наведено в лекції 18. Якщо дві випадкові величини та корельовані 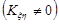, то вони завжди залежні.

4. Додавання сталих до випадкових величин не змінюють кореляційного моменту цих величин, тобто, якщо 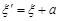та 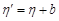, де a та b – сталі, то .

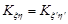Доведення. За означенням кореляційного моменту

.

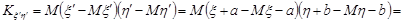
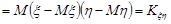5. Якщо випадкові величини 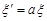та 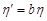, a та b є сталими, що не дорівнюють нулю, то .

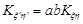Доведіть цю властивість самостійно.

6. Коефіцієнт кореляції випадкових величин та за абсолютною величиною не перевищує добутку стандартних відхилень цих випадкових величин, тобто

.

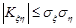Доведення. Візьмемо очевидну нерівність:

.

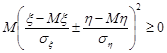Розпишемо цю нерівність:

=

.

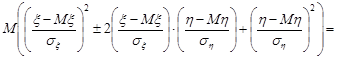
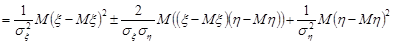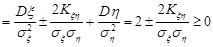Із останньої нерівності випливає властивість 6.

Властивість 6 можна довести також за допомогою нерівності Коші-Буняковського.

Зауважимо також, що коефіцієнт кореляції є величина розмірна, її розмірність визначається добутком розмірностей випадкових величин. Це ускладнює використання кореляційного моменту для оцінки ступені залежності випадкових величин. Цих недоліків не має коефіцієнт кореляції.