Математичне сподівання та дисперсії компонент випадкового вектора. Умовне математичне сподівання та умовна дисперсія
На імовірнісному просторі 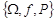 розглянемо випадковий вектор
розглянемо випадковий вектор  .
.
Означення 17.1. Математичним сподіванням випадкового вектора  називається вектор
називається вектор 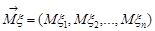 , де
, де 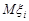 є математичним сподіванням компоненти
є математичним сподіванням компоненти 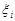 .
.
Геометрично математичне сподівання випадкового вектора можна вважати точкою з координатами 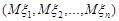 , навколо якої групуються можливі значення
, навколо якої групуються можливі значення 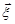 . Часто цю точку називають центром розсіювання.
. Часто цю точку називають центром розсіювання.
Для знаходження координат центра розсіювання дискретного випадкового вектора у випадку n =2 користуються формулами:

Математичні сподівання компонент неперервного випадкового вектора  обчислюємо за формулами:
обчислюємо за формулами:
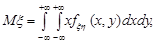

У загальному випадку n-вимірного випадкового вектора математичні сподівання компонент цього вектора обчислюємо так:
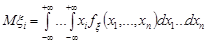 ,
, 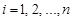 .
.
Дисперсії компонент випадкового вектора  характеризують розсіювання компонент у напрямі відповідної координатної осі. Так у випадку двовимірного дискретного вектора
характеризують розсіювання компонент у напрямі відповідної координатної осі. Так у випадку двовимірного дискретного вектора  дисперсія компоненти
дисперсія компоненти  означає розсіювання відносно осі OX. Її знаходимо за формулою
означає розсіювання відносно осі OX. Її знаходимо за формулою
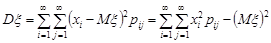 .
.
Аналогічно дисперсію компоненти  , яка означає розсіювання відносно осі OY, обчислюємо за формулою
, яка означає розсіювання відносно осі OY, обчислюємо за формулою
 .
.
У випадку двовимірного неперервного вектора  дисперсії компонент необхідно обчислювати за формулами:
дисперсії компонент необхідно обчислювати за формулами:
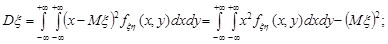
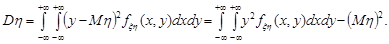
Останні формули узагальнюються на випадок n-вимірного випадкового вектора так:
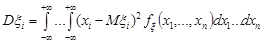 ,
, 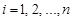 .
.
По відношенню до умовних законів розподілу випадкових величин можна ввести поняття умовного математичного сподівання та умовної дисперсії. Розглянемо спочатку систему двох дискретних випадкових величин  .
.
Означення 17.2. Умовним математичним сподіванням дискретної випадкової величини  при
при 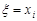 , де
, де 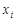 – одне з можливих значень
– одне з можливих значень  , називають величину
, називають величину
М 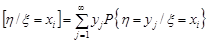 , (17.1)
, (17.1)
де  – значення, яких може набувати випадкова величина
– значення, яких може набувати випадкова величина  . Аналогічно розглядають величини
. Аналогічно розглядають величини
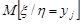
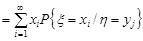 .
.
Аналогічно вводять умовне математичне сподівання для системи неперервних випадкових величин  .
.
Означення 17.3. Умовними математичними сподіваннями неперервних випадкових величин  та
та  називають величини, які обчислюють за формулами:
називають величини, які обчислюють за формулами:
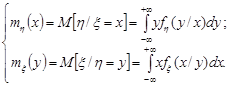 (17.2)
(17.2)
Умовне математичне сподівання  називають регресією величини
називають регресією величини  відповідно до величини
відповідно до величини  , відповідно умовне математичне сподівання
, відповідно умовне математичне сподівання 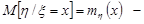 регресією
регресією  відповідно до
відповідно до  .
.
Графіки функцій 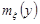 та
та 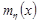 називають лініями регресії
називають лініями регресії  на
на  та
та  на
на  відповідно.
відповідно.
Означимо умовні дисперсії для системи двох випадкових величин  .
.
Означення 17.3. Умовною дисперсією випадкової величини  при умові, що випадкова величина
при умові, що випадкова величина 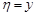 називають
називають
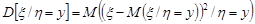 .
.
Аналогічно визначають 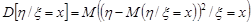 .
.
Отже, умовні дисперсії вводять аналогічно за звичайними формулами для обчислення дисперсії, в яких замість імовірності подій або щільності розподілу записують умовні ймовірності або умовні щільності розподілу в залежності від того дискретна чи неперервна система випадкових величин  задана, а замість математичних сподівань – умовні математичні сподівання.
задана, а замість математичних сподівань – умовні математичні сподівання.
Приклад 17.1. Система дискретних випадкових величин  задана таблицею розподілу (табл. 17.1).
задана таблицею розподілу (табл. 17.1).
Таблиця 17.1

| 
| ||
| 0,1 | 0,3 | ||
| 0,2 | 0,1 | 0,3 |
Знайти умовне математичне сподівання компоненти  за умови, що
за умови, що  набула значення одиниці.
набула значення одиниці.
Розв’язання. Умовне математичне сподівання 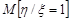 обчислимо за формулою (17.1):
обчислимо за формулою (17.1):
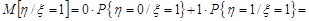
 .
.
Зазначимо, що має місце формула повного математичного сподівання:
1) для системи двох дискретних випадкових величин
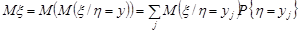 та
та
 ;
;
2) для системи двох неперервних випадкових величин
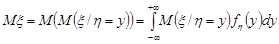 та
та
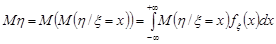 .
.
Приклад 17.2. Випадковий вектор 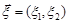 є рівномірно розподіленим в області D = {
є рівномірно розподіленим в області D = { 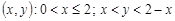 }. Знайти умовні математичні сподівання компонент
}. Знайти умовні математичні сподівання компонент 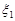 та
та 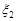 .
.
Розв’язання. За умовою задачі щільність розподілу 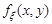 випадкового вектора
випадкового вектора  дорівнює:
дорівнює:
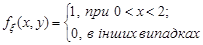
За формулами (15.4) знайдемо щільності розподілу окремих компонент випадкового вектора.

Аналогічно
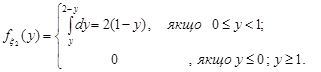
Умовні щільності розподілу компонент випадкового вектора  знайдемо за формулами (16.2) та (16.3).
знайдемо за формулами (16.2) та (16.3).
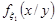
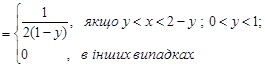
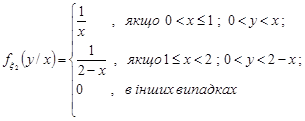
Доречно перевірити отримані результати. Для цього перевіримо умову нормування для щільностей розподілу.
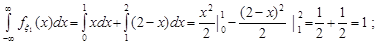
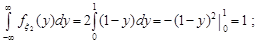
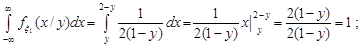
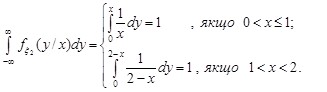
За формулами (17.2) знайдемо умовні математичні сподівання компонент випадкового вектора

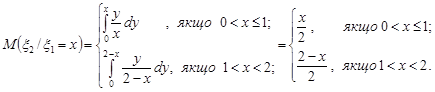 За формулою повного математичного сподівання
За формулою повного математичного сподівання
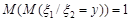 та
та
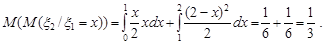
Легко перевірити, що ці результати співпадають із безумовними математичними сподіваннями окремих компонент цього випадкового вектора. Дійсно
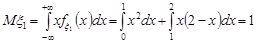 .
.
Аналогічно
 .
.
17.2. Мішані та центральні мішані моменти випадкових векторів
Означення 17.4. Мішаним моментом порядку 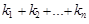 випадкового вектора
випадкового вектора 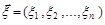 називають величину
називають величину

Мішаним центральним моментом порядку 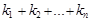 випадкового вектора
випадкового вектора 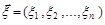 називають величину
називають величину

Якщо випадковий вектор 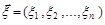 – дискретний із рядом розподілу
– дискретний із рядом розподілу
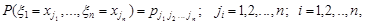
то формули для обчислення моментів набувають вигляду:
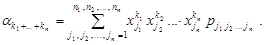
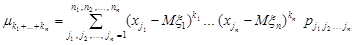 .
.
У випадку неперервного випадкового вектора  із щільністю розподілу
із щільністю розподілу  формули для обчислення моментів мають вигляд:
формули для обчислення моментів мають вигляд:
 .
.
 Внаслідок того, що деякі закони розподілу повністю або майже повністю визначаються своїми моментами першого та другого порядків, то саме ці моменти мають найбільш важливе значення. Так математичне сподівання та дисперсії окремих компонент випадкового вектора є окремими випадками моментів першого та другого порядку.
Внаслідок того, що деякі закони розподілу повністю або майже повністю визначаються своїми моментами першого та другого порядків, то саме ці моменти мають найбільш важливе значення. Так математичне сподівання та дисперсії окремих компонент випадкового вектора є окремими випадками моментів першого та другого порядку.
Більший інтерес ніж дисперсії при розгляданні випадкових векторів мають мішані центральні моменти другого порядку. Зробимо означення.
Означення 17.5. Мішаний центральний момент другого порядку випадкового вектора  , що дорівнює
, що дорівнює
 (17.3)
(17.3)
називається кореляційним моментом (або коваріацією) випадкових величин 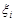 та
та 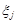 ,
, 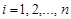 ,
, 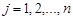 ,
,  .
.
Ясно, що коли 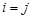 , то
, то  . Таким чином, дисперсії окремих компонент є окремим випадком кореляційних моментів.
. Таким чином, дисперсії окремих компонент є окремим випадком кореляційних моментів.
Всі кореляційні моменти (17.3) компонент випадкового вектора 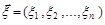 записують у вигляді матриці, яку називають кореляційною матрицею
записують у вигляді матриці, яку називають кореляційною матрицею
K = 
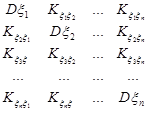
 .
.
Ця матриця завжди симетрична, оскільки  ., по головній діагоналі якої стоять дисперсії окремих компонент.
., по головній діагоналі якої стоять дисперсії окремих компонент.
Розглянемо властивості кореляційного моменту на прикладі системи двох випадкових величин  .
.
Дата добавления: 2016-11-02; просмотров: 3281;
