Перевод целых чисел. Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения

ИНФОРМАЦИОННО-ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ

Системы счисления

Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).

Различают позиционные и непозиционные системы счисления. В позиционных системах каждая цифра числа имеет определенный вес, зависящий от позиции цифры в последовательности, изображающей число. Позиция цифры называется разрядом. В позиционной системе счисления любое число можно представить в виде:

A_n=a_m-1a_m-2…a_ia₀*a_-1a_-2…a_-k=a_m-1*N^m-1+a_m-2*N^m-2…+a_-k*N^-k

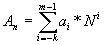, (2.1)

где a_i – i-я цифра числа; k – количество цифр в дробной части числа; m - количество цифр в целой части числа; N – основание системы счисления.

Основание системы счисления N показывает, во сколько раз “вес” i-го разряда больше (i-1) разряда. Целая часть числа отделяется от дробной части точкой (запятой).

Любое число Х в позиционной системе счисления можно записать как X+k^p *M , где М – мантисса, Р- порядок. В ЭВМ с целью упрощения вычислений «.» фиксируется либо перед старшим либо после младшего разряда.

Пример 1.1.А₁₀=37.25.

В соответствии с формулой (2.1)это число формируется из цифр с весами рядов:

А₁₀=3*10¹+7*10⁰+2*10^-1+5*10^-2.

Теоретически наиболее экономичной системой счисления является система с основанием е=2,71828..., находящимся между числами 2 и 3.

Во всех современных ЭВМ для представления числовой информации используется двоичная система счисления. Это обусловлено:

более простой реализацией алгоритмов выполнения арифметических и логических операций;

более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);

экономичностью аппаратурной реализации всех схем ЭВМ.

При N=2 число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления широкое распространение получили и производные системы:

• десятичная, точнее двоично-десятичное представление десятичных чисел, - {0, 1,...,9};

• шестнадцатеричная - {0,1,2, ...9, А, В, С, D, Е, F}. Здесь шестнадцатеричная цифра А обозначает число 10,В-число 11, ...,F-число 15;

• восьмеричная (от слова восьмерик) - {0,1,2,3,4,5, 6, 7}. Она широко используется во многих специализированных ЭВМ.

Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как 16 = 2⁴ и 8 = 2³. Они используются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков.

Перевод целых чисел

Целое число с основанием N₁ переводится в систему счисления с основанием N₂ путем последовательного деления числа An1, на основание N₂ , записанного в виде числа с основанием N₁, до получения остатка. Полученное частное следует вновь делить на основание N₂, и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя. Полученные остатки от деления и последнее частное записываются в порядке, обратном полученному при делении. Сформированное число и будет являться числом с основанием N₂.

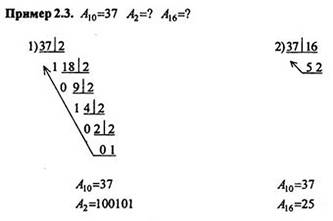
Проверку правильности перевода можно выполнить используя веса разрядов.

32 16 8 4 2 1 16 1

1 0 0 1 0 1 = 1+4+32 =37 2 5 =16*2+5=37

Так как восьмеричная и шестнадцатиричная системы являются производными от двоичной системы, то перевод может быть осуществлен еще более проще.

Для перевода числа из двоичной системы в восьмичичную, двоичное число разбивается на триады, и каждая двоичная триада записывается в виде десятичной цифры.

100 101 = 45₈

Для перевода числа из двоичной системы в шестнадцатеричную, двоичное число разбивается на тетрады и каждая двоичная тетрада записывается в виде десятичной цифры.

10 0001 = 25_f