Перевод дробных чисел. Дробное число с основанием N1 переводится в систему счисления с основанием N2 путем последовательного умножения An1 на основание N2

Дробное число с основанием N₁ переводится в систему счисления с основанием N₂ путем последовательного умножения A_n1 на основание N₂, записанное в виде числа с основанием N₁. При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность полученного результата, представляющего число A_n1 в системе счисления N₂.

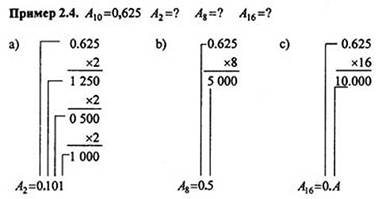
Проверку правильности перевода можно выполнить используя веса разрядов Веса разрядов _{0,5 0,25 0,125 0,0625}

, 1 0 1

А₁₀= 0,5+0,125=0,625;

1/8 1/64 1/512 …

А₁₀= 1/8*5=0,625

1/16 1/256

А₁₀₌ А*1/16=10*1/16=0,625

Представление чисел в различных системах счисления допускает однозначное преобразование их из одной системы в другую. В ЭВМ перевод из одной системы в другую осуществляется автоматически по специальным программам. Правила перевода целых и дробных чисел отличаются.

В двоично-десятичной системе счисления каждая десятичная цифра записывается в двоичном коде с помощью четырех бит.

А₁₀ = 456

4 5 6

А_2-10 = 100 0101 0110

Поскольку двочная система явяляется позиционной системой счисления, то возможно перевод из десятичной системы в двоичную с помощью весов разрядов.

1. Определяем количество разрядов n >= log₂ A₁₀. Так как нумерация разрядов начинается с нуля, то вес максимального разряда будет вычисляться 2ⁿ^-1.

2. Проставляем 1 в старшем разряде. Вычитаем из числа вес разряда и переходим к боле младшему разряду.

3. Сравниваем значение числа с весом текущего разряда. Если значение числа больше веса разряда, то проставляем в соответствующем разряде 1 и вычитаем из числа вес разряда, иначе проставляем в соответствующем разряде 0. Переходим к боле младшему разряду.

4. Пункт 3 повторяем до заполнения значениями все разряды числа.

Пример.

А₁₀= 45.

1. n>= log₂45 = 6.

2. ® 1, А₁₀= 45 -32 = 13

3. 13 < 16 ® 0

4. 13 > 8 , ® 1, А₁₀=16 – 13 =5

5. 5 > 4 ® 1 , А₁₀= 5 – 4

6. 1 < 2 , ® 0

7. 1=1, ® 1

Полученное число А₂= 101101. Проверка А₁₀ = 32+8+4+1 = 45.

Перетворення методом Горнера

Для того, щоб перетворювати числа з двійкової в десяткову систему даним методом, треба cкласти цифри зліва направо, перемножуючи раніше отриманий результат на основу системи (в даному випадку 2).

1) 0*2+1=1

2) 1*2+1=3

3) 3*2+1=7

4) 7*2+1=15

5) 15*2+1=31

6) 31*2+0=62

7) 62*2+1=125

8) 125*2+0=250

9) 250*2+0=500

10) 500*2+0=1000

11) 1000*2+0=2000

12) 2000*2+1=4001

13) 4001*2+1=8003

14) 8003*2+1=16007

11111010000111₂16007₁₀

Дата добавления: 2016-10-17; просмотров: 680;