Основные соотношения размерных цепей

Размерная цепь всегда замкнута. На основании этого свойства установлена зависимость, которая связывает номинальные размеры звеньев. Для плоских размерных цепей по номинальным значениям эта зависимость выражается формулой:

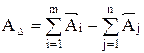, (5.1)

где m и n – число увеличивающих и уменьшающих звеньев соответственно.

Для определения зависимости, которая связывает допуски звеньев в размерной цепи, первоначально нужно определиться с предельными значениями исходного звена. Очевидно, что они будут вычисляться по формулам:

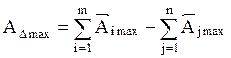
	(5.2)
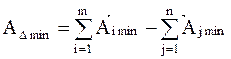.	(5.3)

Если почленно вычесть значения А_Δmax и А_Δmin в формулах (5.2), (5.3) и учесть то, что разница предельных значений не что иное как допуск, то получится выражение:

.

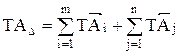(5.4)

Окончательно можно получить:

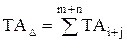
(5.5)

Из формулы (5.5) видно, что величина допуска замыкающего звена равна сумме допусков составляющих звеньев. Поэтому чтобы обеспечить наибольшую точность замыкающего звена, размерная цепь должна состоять из возможно меньшего числа звеньев, т. е. должен соблюдаться принцип наикратчайшей размерной цепи.

Если последовательно вычесть из уравнений (5.2) и (5.3) выражение (5.1), то получатся зависимости, по которым определяются верхнее и нижнее предельные отклонения исходного звена:

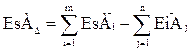;	(5.6)
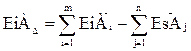,	(5.7)

где Es и Ei – верхнее и нижнее предельные отклонения соответствующих звеньев.

Координата середины поля допуска замыкающего звена рассчитывается следующим образом:

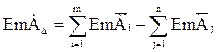. (5.8)

Величина допуска в соответствии с требованиями ГОСТ 25346-89 для большинства квалитетов определяется по формуле:

IT = ai, (5.9)

где IT – обозначение допуска без соотнесения к конкретной системе допусков и виду размера;

а – число единиц допуска, определенное для данного квалитета;

i – единица допуска, зависящая от размера.

Применительно к расчетам размерной цепи формулу (5.9) лучше записать в виде:

TA = a i. (5.10)

Значения i и a можно выбрать из табл. 3.1 и 3.2.