Задача о переговорах
На рисунке ниже изображен треугольник, представляющий множество векторов выигрышей, реализуемых при различных совместных смешанных стратегиях. Угловые точки этого треугольника – это выигрыши, соответствующие четырем возможным исходам игры в чистых стратегиях (два из этих исходов совпадают).
Внутренние точки треугольника представляют собой возможные исходы переговоров между игроками о выборе совместной смешанной стратегии. Поскольку каждый из игроков имеет в своем распоряжении максиминную стратегию, которая обеспечивает ему выигрыш в 2/3 вне зависимости от действий другого игрока, то он никогда не согласиться на получение меньшего выигрыша. По этой причине в результате переговоров могут быть реализованы не все точки треугольника, а только точки, заключенные внутри фигуры ABECD, обеспечивающие каждому из игроков выигрыш не менее его максимина. Указанное множество называется переговорным.
Ясно, что игрокам нет смысла выбирать не оптимальные по Парето точки. Значит, переговорное множество фактически сокращается до отрезка АВ. Задача выбора точки из переговорного множества называется задачей о переговорах. Для решения этой задачи можно предложить различные арбитражные схемы. Наиболее известной является арбитражная схема Нэша. Схема Нэша базируется на системе аксиом, одной из которых является аксиома о равноправии партнеров. Поэтому схема Нэша дает в нашем случае в качестве решения середину отрезка АВ.
Аксиома о равноправии игроков является формальным выражением идеи справедливости. Однако эта аксиома далеко не всегда принимается сторонами реальных переговоров, поэтому схема Нэша имеет скорее теоретический интерес.
Задачи:
Найти ситуации равновесия по Нэшу и Парето-оптимальные ситуации:
1) 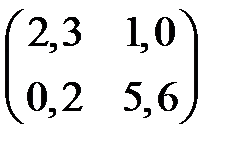 2)
2) 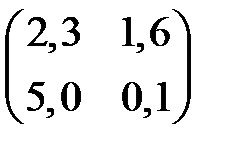 3)
3) 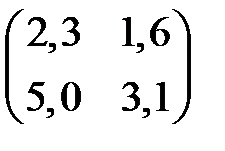 4)
4) 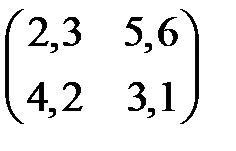
5) Существуют ли сильно равновесные ситуации в играх 1-4?
6) Рассматривая игры 1-4 как бескоалиционные, найти ситуации равновесия по Нэшу в смешанных стратегиях.
7) Рассматривая игры 1-4 как коалиционные, найти в них переговорные множества
Дата добавления: 2016-10-17; просмотров: 1039;
