Принципы оптимальности в бескоалиционных играх

Известно, что для антагонистических игр принципы минимакса, максимина и равновесия совпадают (если они реализуемы, т. е. существует равновесие, а максимин и минимакс достигаются). В таком случае они определяют единое понятие оптимальности и решения игры. В теории неантагонистических игр нет единого подхода к выработке принципов оптимальности. По существу имеется целое множество таких принципов, каждый из которых основывается на некоторых дополнительных предположениях о поведении игроков и структуре игры.

Естественно предположить, что в игре G каждый из игроков стремится к достижению ситуации r, в которой значение его функции полезности (выигрыша) было бы наибольшим. Однако функция выигрыша v_i зависит не только от стратегии i-го игрока, но и от стратегий, выбираемых другими игроками, поэтому ситуации, дающие большее значение выигрыша для i-го игрока, могут не быть таковыми для других игроков. Таким образом, так же как и в случае антагонистической игры, стремление игроков получить наибольший выигрыш носит конфликтный характер и сама формулировка того, какое поведение является «хорошим» или оптимальным в игре, является проблематичной. Здесь имеется несколько подходов. Одним из них является равновесие по Нэшу и его различные обобщения. В случае, когда игра G является антагонистической, равновесие по Нэшу совпадает с понятием равновесия, которое представляет собой основной принцип оптимальности в антагонистической игре.

Пусть 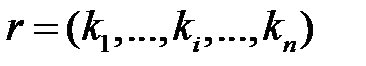— произвольная ситуация в игре G, a k_i — некоторая стратегия игрока i. Построим ситуацию, которая отлична от r только тем, что стратегия k_i игрока i заменена на стратегию 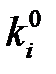. В результате мы получаем ситуацию 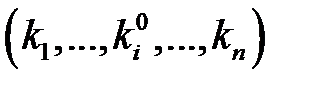, которую будем обозначать через 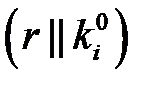. Очевидно, что если k_i и 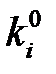совпадают, то .

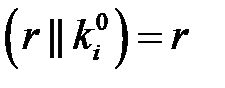Определение. Ситуация 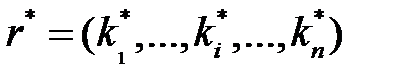называется ситуацией равновесия по Нэшу, если для любого игрока 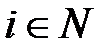и любой его альтернативы 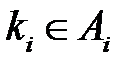имеет место неравенство

(3.2)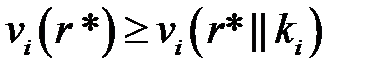

Множество ситуаций, равновесных по Нэшу в игре G, будем обозначать NE(G). Тот факт, что r* равновесна по Нэшу будем записывать как .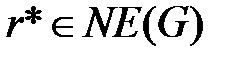

Из определения ситуации равновесия по Нэшу следует, что ни один из игроков i не заинтересован в отклонении от стратегии , входящей в эту ситуацию (согласно (3.2) его выигрыш при использовании другой стратегии разве лишь уменьшится при условии, что остальные игроки придерживаются стратегий, образующих ситуацию равновесия r*). Таким образом, если игроки договорились предварительно об использовании стратегий, входящих в ситуацию равновесия r*, то индивидуальное отклонение от договора невыгодно отклонившемуся игроку.

Определение. Стратегия называется равновесной, если она входит хотя бы в одну ситуацию равновесия по Нэшу.

Для биматричной -игры G(A, В) пара (i*, j*) будет ситуацией равновесия по Нэшу ( 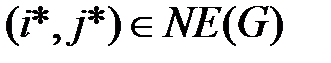), если неравенства

(3.3)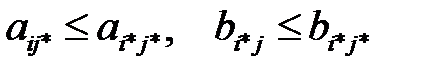

выполняются для всех номеров строк 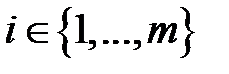и столбцов 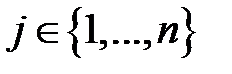. Так, в игре «семейный спор» равновесными являются ситуации (1,1) и (2,2), в игре «перекресток» — (1,2) и (2,1).

Сопоставим понятия равновесия для антагонистических матричных и неантагонистических биматричных игр.

Для антагонистической игры пара (i*, j*) является ситуацией равновесия, если

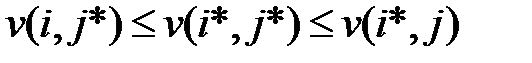
При этом имеют место следующие основные свойства антагонистических игр.

1. Игроку невыгодно информировать своего противника о стратегии (чистой или смешанной), которую он собирается применить. (Конечно, если игрок собирается использовать оптимальную стратегию, то его выигрыш не уменьшится от того, что он объявит об этом, но он ничего и не выигрывает.)

2. Если (i,j) и (k,l) — ситуации равновесия в игре, то ситуациями равновесия являются также ситуации (i,l), (k,j) и

(3.4)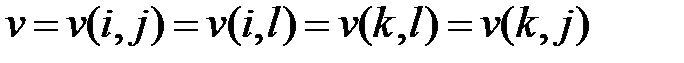

3. Игроки не заинтересованы в общении перед началом игры для выработки совместных действий.

4. Если в игре существует ситуация равновесия, а i* — максиминная и j* — минимаксная стратегии соответственно 1 и 2 игроков, то (i*,j*) — ситуация равновесия, и наоборот.

Выясним, выполняются ли эти свойства для биматричных игр.

Рассмотрим игру «семейный спор» (см. пример 1). Как уже отмечалось, в ней есть две равновесные ситуации (1,1) и (2,2). Однако выигрыши игроков в этих ситуациях различны, что противоречит (3.4). Далее заметим, что, несмотря на равновесность ситуаций (1,1) и (2,2), пары (1,2) и (2,1) не являются ситуациями равновесия по Нэшу, т. е. свойство 2 не выполнено полностью.

Если игрок 1 информирует партнера о намерении выбрать стратегию 1, и если игрок 2 убежден, что тот будет упорствовать, то ему ничего не остается, как объявить первую стратегию. Аналогичные рассуждения можно провести и за игрока 2. Таким образом, каждому из игроков выгодно первому объявить свою стратегию, что противоречит свойству 1 для антагонистических игр.

Предположим, что игроки не общаются до начала игры, а делают выбор одновременно и независимо друг от друга (как и предусмотрено правилами бескоалиционной игры). Проведем рассуждения за игрока 1. Ему выгодно, чтобы реализовалась ситуация (1,1) с выигрышами {2,1}. Но игроку 2 выгодна ситуация (2,2) с выигрышами {1,2}. Поэтому, если игрок 1 выберет стратегию 1, то игрок 2 может выбрать стратегию 2, и они оба проиграют (вектор выигрышей {0, 0}). Тогда игроку 1 имеет смысл выбрать стратегию 2, поскольку в ситуации (2,2) он получает выигрыш 1. Но игрок 2 может рассуждать аналогично и выбрать 1, тогда в ситуации (1,2) они оба опять проиграют.

Таким образом, имеет место случай, когда ситуация выгодна (и поэтому неустойчива) для игрока 1. Аналогично (с точки зрения игрока 2) можно исследовать ситуацию (2,2). Поэтому игрокам выгодно общаться перед началом игры и договариваться о совместном плане действий, что противоречит свойству 3. Затруднения возникают также из-за того, что пара максиминных стратегий не является равновесной (противоречит свойству 4).

Таким образом, имеется пример игры, когда не выполнено ни одно из свойств 1 — 4 антагонистической игры.

Итак, в различных ситуациях равновесия по Нэшу векторы выигрышей игроков могут быть различны. Кроме того, множество ситуаций равновесия по Нэшу в отличие от множества ситуаций равновесия в антагонистической игре не является прямоугольным. Ситуация равновесия по Нэшу является множественным принципом оптимальности в том смысле, что различные ситуации равновесия могут быть в разной степени предпочтительными для различных игроков. Таким образом, остается не решенным вопрос: какую из ситуаций равновесия можно принять как устраивающий всех игроков принцип оптимальности? В дальнейшем будет показано, что множественность принципа оптимальности является существенной характерной чертой оптимального поведения в конфликтных управляемых процессах со многими участниками.

Пусть 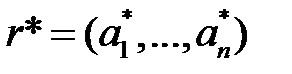- ситуация равновесия по Нэшу. В отличие от антагонистического случая равновесная стратегия i-го игрока 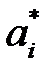далеко не всегда обеспечивает получение, по крайней мере, выигрыша 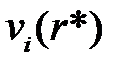, поскольку это существенно зависит от того, выберут ли остальные игроки стратегии, входящие в ситуацию равновесия по Нэшу. Поэтому равновесную стратегию не следует трактовать как оптимальную стратегию i-го игрока. Такая трактовка осмыслена только для набора стратегий игроков, т. е. для ситуаций.

Важная особенность ситуации равновесия по Нэшу заключается в том, что отклонение от нее двух игроков и более может привести к увеличению выигрыша хотя бы одного из отклонившихся игроков. Пусть 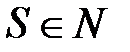— некоторое подмножество множества игроков (коалиция) и пусть 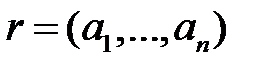— ситуация в игре G. Обозначим через 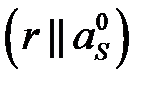— ситуацию, которая получается из ситуации r при замене в ней стратегий . Иными словами, в ситуации 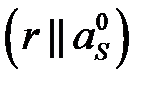игроки, входящие в коалицию S, заменяют свои стратегии на другие. Если r* — ситуация равновесия по Нэшу, то из (3.3) вовсе не следует, что

(3.5)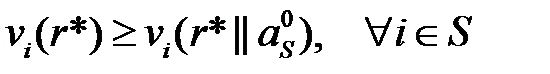

Например, в игре «дилемма заключенного» (ДЗ) имеется ситуация равновесия по Нэшу – (конфликт, конфликт). Ни одному из игроков невыгодно отклоняться от этой ситуации в одиночку. Однако, если оба игрока одновременно сменят свои действия на «сотрудничество», то оба увеличат свой выигрыш.

Можно усилить понятие равновесия по Нэшу, потребовав выполнения условия (3.5) или ослабленного условия (3.5), требуя уменьшения выигрыша хотя бы для одного из игроков коалиции S при отклонении от ситуации равновесия.Тогда мы приходим к следующему определению.

Определение. Ситуация r* называется сильно равновесной, если 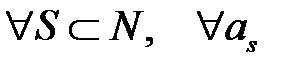, выполняется неравенство

(3.6)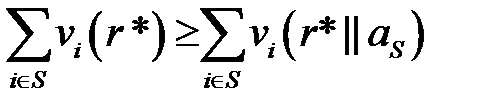

Условие (3.6) гарантирует нецелесообразность соглашения между игроками с целью вступления в некоторую коалицию S, так как в любой коалиции находится игрок j, которого это соглашение не устраивает. Любая сильно равновесная ситуация является равновесной.

Если бы сильное равновесие существовало в достаточно широком классе игр, то оно могло бы явиться приемлемым принципом оптимальности в бескоалиционной игре. Однако оно существует крайне редко.

В игре ДЗ ситуация равновесия (K,K) не является сильно равновесной. Она дает игрокам вектор выигрышей {0,0}. Однако если оба игрока сыграют (C,C), то они получат вектор выигрышей {5, 5}, что выгодно обоим. Эта ситуация не является равновесной, но она лучше равновесной для обоих игроков.

Последнее рассуждение приводит к мысли о возможности других принципов оптимальности в бескоалиционной игре, приводящих к ситуациям, более выгодным обоим участникам, чем в случае равновесных ситуаций. Таким принципом оптимальности является оптимальность по Парето.

Рассмотрим множество векторов-выигрышей игроков во всех возможных ситуациях , где 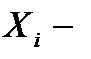множество стратегий i-го игрока.

Определение. Ситуация 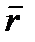в бескоалиционной игре G называется оптимальной по Парето, если не существует ситуации rÎR, для которой имеют место неравенства

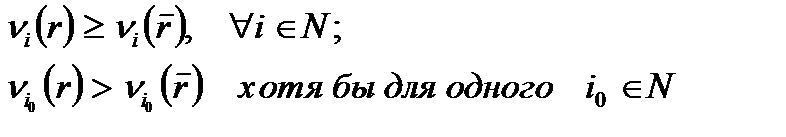
В игре ДЗ ситуация (С,С) с выигрышами {5,5} является оптимальной по Парето, но не равновесной.

Содержательное различие понятий ситуации равновесия и ситуации, оптимальной по Парето, состоит в следующем. В первой ситуации ни один игрок, действуя в одиночку, не может увеличить своего выигрыша, во второй — все игроки, действуя совместно, не могут (даже не строго) увеличить выигрыш каждого.

Заметим также, что соглашение о выборе фиксированной ситуации равновесия удерживает каждого индивидуального игрока от отклонения от нее. В оптимальной по Парето ситуации отклонившийся игрок может в некоторых случаях получить существенно больший выигрыш. В то же время сильно равновесная ситуация безусловно является и оптимальной по Парето. Так, в ДЗ ситуация (К,К) равновесна, но не оптимальна по Парето. Вместе с тем ситуация (С,С), наоборот, оптимальна по Парето, но не является равновесной. В игре «семейный спор» обе равновесные ситуации (1,1) и (2,2) сильно равновесны и оптимальны по Парето, но, как уже отмечено, не являются взаимозаменяемыми.

Такая же картина имеет место и в игре «перекресток».В этой игре ситуации (1,2), (2,1) равновесны и оптимальны по Парето (ситуация (2,2) оптимальна по Парето, но не равновесна). Для каждого игрока равновесной является стратегия «остановиться», если другой игрок решил проехать перекресток, и, наоборот, выгодно выбрать стратегию «ехать», если другой игрок остановился. Однако выигрыш в 5 единиц каждый из игроков получает только при выборе стратегии «ехать», поэтому здесь неизбежна борьба за лидерство, т. е, каждый из игроков заинтересован первым заявить, что он выбрал стратегию «ехать».

Заметим, что точно к такому же выводу мы пришли при анализе игры «семейный спор».

Можно анализировать поведение «лидер – ведомый» в игре двух лиц G = (X,Y; 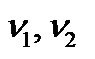). Обозначим множества наилучших решений игроков как

R =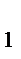

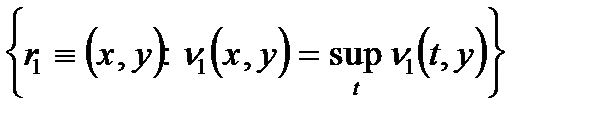
R =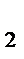

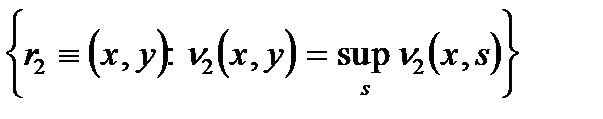
Определение. Ситуацию 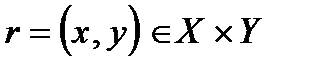называют i-равновесной по Штакельбергу в игре двух лиц, а 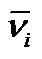i-выигрышем, если 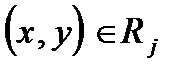и выполняется равенство 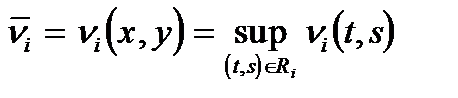, где i =1,2, i¹j .

Понятие i-равновесия по Штакельбергу можно интерпретировать так: лидер (игрок 1) знает функции выигрыша обоих игроков 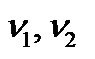, а тем самым и множество наилучших решений (ответов) R 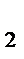игрока 2 (ведомого) на любую стратегию игрока 1. Тогда он, обладая этой информацией, максимизирует свой выигрыш, выбирая стратегию из условия вышеприведенного равенства. Таким образом, 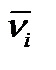- это выигрыш i-го игрока, действующего оптимально в качестве «лидера» в игре G.

Определение. Говорят, что в игре двух лиц имеет место борьба за лидерство, если не существует такой ситуации 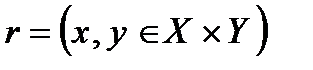, что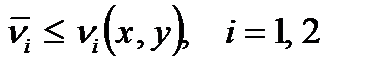

Сформулируем без доказательства следующее утверждение. Если бескоалиционная игра G двух лиц имеет по крайней мере две оптимальных по Парето и равновесных по Нэшу ситуации 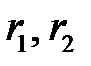с различными векторами выигрышей

то в игре G имеет место борьба за лидерство.