Передаточные функции.

Понятие передаточная функция является наиболее важной категорией в теории автоматического управления и регулирования. Пере­даточная функция является своего рода математической моделью САР, т.к. полностью характеризует динамические свойства системы.

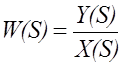Передаточная функция представляет собой отношение изображе­ние по Лапласу выходной величины Y ( S ) к изображению входной величины Х ( S ), т.е.

.

Учитывая условия 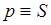для линейных систем уравнение (2.3) запишем в следующем виде:

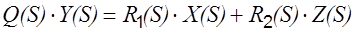. (2.8)

Поскольку для линейных систем можно применить принцип наложения, то будет справедливым выделить следующие два случая:

- сигнал Z ( S ) = 0, тогда ;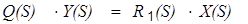

- сигнал X ( S ) = 0, тогда .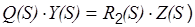

Тогда, для любой САР, имеющей входы по управлению и по возмущению, можно определить две передаточные функции

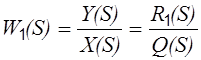, (2.9)

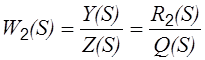. (2.10)

Уравнение (2.9) представляет передаточную функцию по управлению, а выражение (2.10) представляет передаточную функцию по возмущению.

Как известно, собственный оператор Q ( p ) может быть записан в следующем виде

.

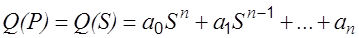Соответственно оператор управляющего воздействия R₁ ( р ) и опе­ратор возмущающего воздействия R₂ ( p ) выразим следующим образом:

;

.

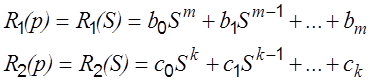Следовательно, передаточные функции по управлению и по возмущению представляют собой отношения следующих полиномов:

;

.

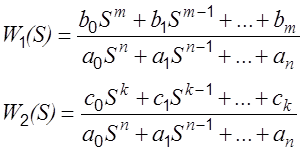Для физической реализуемости системы необходимо выполнить условие n>m и n>k.

Передаточные функции содержат особые точки на комплексной плоскости -нули и полюса. Полюса - это те значения S, при которых передаточная функция превращается в бесконечность. Для определения полюсов необходимо собственный оператор (знаменатель передаточной функции) приравнять к нулю и произвести решение алгебраического уравнения относительно S. Нули - это те значения S, при которых передаточная функция равна нулю. Для нахождения нулей числитель передаточной функции приравнивается к нулю и полученное алгебраическое уравнение решается относительно S. В связи о этим передаточная функция может быть представлена как отношение произведений элементарных сомножителей

,

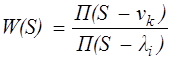где l_i - полюса передаточной функции;

n_k - нули передаточной функции.

Если задана структура САР, то можно определить передаточную функцию относительно любых двух точек структуры. При этом необ­ходимо использовать существующие правила и метода структурных преобразований.