Информация и информационные процессы. 4 страница

A_q = a_n-1 · q^n-1 + . . . + a₁ · q¹ + a₀ · q⁰ + a_-1 · q^-1 + a_-2 · q^-2 + . . . + a_-m · q^-m

Пользуясь формулой для числа, записанного в системе с основанием, не равным 10, можно найти его десятичный эквивалент. При этом учитываем, что 1 и 0 - цифры, имеющие одинаковый смысл в любой системе счисления.

Пример 1.

A₈ = 132; A₁₀ = ?;

A₁₀ = 132₈ = (1 · 8² + 3 · 8¹ + 2 · 8⁰)₁₀ = (64 + 24 + 2)₁₀ = 90₁₀.

Пример 2.

A₂ = 100110; A₁₀ = ?;

A₁₀ = 100110₂ = (1 · 2⁵ + 1 · 2² + 1 · 2¹)₁₀ = (32 + 4 + 2)₁₀ = 38₁₀.

Пример 3.

A₁₆ = A9; A₁₀ = ?;

A₁₀ = A9₁₆ = (10 · 16¹ + 9 · 16⁰)₁₀ = (160 + 9)₁₀ = 169₁₀.

Пример 4.

A₈ = 0,24; A₁₀ = ?;

A₁₀ = 0,24₈ = (2 · 8^-1 + 4 · 8^-2)₁₀ = 0,3125₁₀.

Пример 5.

A₂ = 0,101; A₁₀ = ?;

A₁₀ = 0,101₂ = (1 · 2^-1 + 1 · 2^-3)₁₀ = 0,625₁₀.

Пример 6.

A₁₆ = 0,C; A₁₀ = ?;

A₁₀ = 0,C₁₆ = (12 · 16^-1) ₁₀ = 0,75₁₀.

Обсудите заполненную таблицу с другими студентами группы. Внесите в нее необходимые исправления и дополнения.

Решите следующие задачи: 1.Какое множество понятий однозначно определяет позиционную систему счисления: 1) {базис, алфавит, основание}; 2) {базис, алфавит}; 3) {базис}? 2. Какая последовательность чисел может быть ис­пользована в качестве базиса позиционной системы счисления? 3. Какие символы могут быть использованы в каче­стве цифр системы счисления? 4. В примере 2 были приведены представления чи­сел 10, 25 и 100 в системах счисления, отличных от де­сятичной. Можно ли эти числа записать в указанных систе­мах еще и другим способом или это представление един­ственно? 5. Запишите десятичные представления чисел: 1. 1011001112; 2. 1AC9F16; 3. 17458; 4. 11001,0112; 5. ED4A,C116$ 6. 147,258.

Тема 3.2 Системы счисления. Перевод чисел из одной системы счисления в другую.

Основные понятия: позиционные системы счисления, основание системы счисления, метод триад, метод тетрад.

Условные обозначения:

- задания до чтения текста

- задания во время чтения

- задания после чтения

В теме 3.2 был предложен способ перевода из какой-либо (q-ичной) системы счисления в десятичную. Сформулируйте правило перевода чисел, записанных в системах счисления с основанием q>1, в десятичную систему счисления. Запишите это правило. Приведите примеры.

Прочитайте текст. Во время чтения делайте пометки на полях: «+» - надо запомнить; «-» - думал иначе, «?» - не понял, есть вопросы.

Правила перевода целых чисел   Результатом является целое число. 1. Из десятичной системы счисления - в двоичную и шестнадцатеричную: а. исходное целое число делится на основание системы счисления, в которую переводится (2, 8 или 16); получается частное и остаток; б. если полученное частное не делится на основание системы счисления так, чтобы образовалась целая часть, отличная от нуля, процесс умножения прекращается, переходят к шагу в). Иначе над частным выполняют действия, описанные в шаге а); в. все полученные остатки и последнее частное преобразуются в соответствии с таблицей в цифры той системы счисления, в которую выполняется перевод; г. формируется результирующее число: его старший разряд - полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа - первый остаток от деления, а старший - последнее частное. Пример 1. Выполнить перевод числа 19 в двоичную систему счисления: Пример 2. Выполнить перевод числа 19 в шестнадцатеричную систему счисления: Пример 3. Выполнить перевод числа 123 в шестнадцатеричную систему счисления: 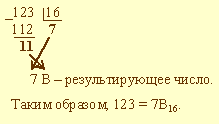2. Из двоичной системы счисления в шестнадцатеричную: а. исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4; б. каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицей. Таблица q=16 A B C D E F q=10 q=2     Пример 4. Выполнить перевод числа 100112 в шестнадцатеричную систему счисления. Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем: В соответствии с таблицей 00112 = 112 = 316 и 00012 = 12 = 116. Тогда 100112 = 1316. 3. Из шестнадцатеричной системы счисления в двоичную: а. каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады; б. незначащие нули в результирующем числе отбрасываются. Пример 5. Выполнить перевод числа 1316 в двоичную систему счисления. По таблице имеем: 116 = 12 и после дополнения незначащими нулями 12 = 00012; 316 = 112 и после дополнения незначащими нулями 112 = 00112. Тогда 1316 = 000100112. После удаления незначащих нулей имеем 1316 = 100112. <1234567> Дата добавления: 2016-09-20; просмотров: 2044; Поиск по сайту: Похожие статьи: 1 страница 1 страница 1 страница 1 страница 1 страница 1 страница 1 страница. АБСЦЕСС ГОЛОВНОГО МОЗГА - очаговое скопление гноя в веществе мозга. Пользователям сайта интересно: Азбука Морзе и дальнейшее развитие телеграфа. Автоматическая телеграфия Развитие фотографических процессов. Пленка, проявление и печатание Энергия. Какие существуют виды энергии Механика. Ньютоновские законы движения. Масса, вес и гравитация Основы геометрии. Линии и углы. Треугольники Как научиться определять расстояние и размеры на-глаз? Оборудование ночлега в походе Генетические признаки. Как передаются характерные черты Интересные факты в истории Западной Европы Клетки и ДНК. Что такое ДНК