Информация и информационные процессы. 3 страница
 - задания во время чтения
- задания во время чтения
 - задания после чтения
- задания после чтения

| Решите задачу 1: На ферме живут 16 цыплят, 7 кур, 1 петух и 5 гусей. Определить количество информации в зрительном сообщении: «На рождество зажарили цыпленка». Решите задачу 2: Мама попросила дочку сходить в магазин и купить фрукты. В магазине в наличии было 4 кг. яблок, 5 кг. груш и 10 кг. апельсинов. Определить количество информации, полученной мамой в зрительном сообщении о покупке, сделанной дочкой. Можно ли решить данную задачу таким же способом, как и предыдущую? Почему? |

| Прочитайте текст. Во время чтения делайте пометки на полях: «!» - важно, «?» - не понятно, есть вопросы | ||||||||||||||||||||||||||||||
В статистической теории информации Шеннона вводится более общая мера количества информации, в соответствии с которой рассматривается не само событие, а информация о нем.
Любое сообщение, несущее информацию, всегда представляет собой совокупность сведений о какой-то физической системе. Например, на вход автоматизированной системы управления производственным цехом может быть подано сообщение о химическом составе сырья, температуре в печи, нормальном или повышенном проценте брака. Каждое из таких сообщений описывает состояние той или иной физической системы.
Так же обстоит дело, когда передается сводка погоды или когда на адрес городского эпидемиолога поступает сообщение о числе заболеваний за сутки. Во всех случаях сообщение описывает состояние физической системы.
Очевидно, если бы состояние этой системы было известно заранее, то не имело бы смысла передавать сообщение: оно не имело бы никакой информации. Сообщение приобретает смысл только тогда, когда состояние системы заранее неизвестно, обладает какой-то степенью неопределенности. Очевидно, сообщение, выясняющее для нас состояние такой системы, будет тем богаче и содержательнее, чем больше была неопределенность системы до этого сообщения.
Возникает естественный вопрос: что значит "большая" или "меньшая" степень неопределенности и как ее можно измерить?
Чтобы уяснить себе этот вопрос, сравним между собой две физические системы, каждой из которых присуща некоторая неопределенность. В качестве первой системы (обозначим ее А) возьмем монету, которая подбрасывается и может случайным образом выпасть той или иной стороной, то есть оказаться в одном из двух состояний:
В качестве второй системы (пусть будет В) возьмем игральный кубик, который тоже подбрасывается и может оказаться в одном из шести состояний:
Какая из этих систем обладает большей неопределенностью? Очевидно, вторая, так как она отличается большим разнообразием возможных состояний. С первого взгляда может показаться, что все дело в числе состояний: у первой системы их два, а у второй - шесть. Однако степень неопределенности зависит не только от числа состояний, но и от их вероятностей. Чтобы убедиться в том, что степень неопределенности зависит от вероятности появления события, рассмотрим третью систему С, у которой, как и у системы А, два возможных состояния. Пусть системой С будет техническое устройство, которое имеет два возможных состояния:
Если вероятности этих двух состояний одинаковы (по 0,5 или 50%), то степень неопределенности системы С такая же, как системы А (монета). Теперь представим себе, что состояния С1 и С2 неравновероятны, например, вероятность первого - 0,99 (99%), а вероятность второго - 0,01 (1%). Очевидно, степень неопределенности такой системы будет гораздо меньше, чем в первом случае: ведь мы почти уверены, что устройство будет исправно. А если состояние С1 будет совершенно достоверно (то есть иметь вероятность 1), то, очевидно, система С вообще никакой неопределенностью обладать не будет. Таким образом, мы убедились, что степень неопределенности физической системы зависит не только от числа состояний, но и от того, как распределены вероятности между состояниями. В теории информации в качестве меры неопределенности системы принята так называемая энтропия. Если система А имеет n возможных состояний
причем вероятности этих состояний равны соответственно
то энтропией системы А называется величина:
или
то есть сумма произведений вероятностей состояний на логарифмы этих вероятностей, взятая с обратным знаком (обратный знак берется просто для того, чтобы энтропия была неотрицательной). Логарифм в формуле (2) может быть взят при любом основании. Обычно логарифм берется по основанию 2. Тогда говорят, что энтропия измеряется в двоичных единицах (битах): Один бит - это энтропия простейшей физической системы, которая может быть только в одном из двух состояний, причем эти состояния равновероятны. Действительно, пусть система А обладает двумя состояниями А1 и А2 с вероятностями p1 = 0,5 и p2 = 0,5. Согласно формуле (2), энтропия такой системы равна
то есть одному биту. За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации. В классической теории информации количество информации, заключенной в сообщении, измеряется уменьшением энтропии системы под действием этого сообщения. Пусть, например, до поступления сообщения энтропия системы была равна двум битам, а после него стала равной одному биту. Из этого мы заключаем, что информация, заключенная в сообщении, равна одному биту. Понятию "информация в битах" можно дать очень наглядное истолкование: она равна числу ответов "да" и "нет" на разумно поставленные вопросы, с помощью которых можно получить ту же информацию. Пусть, например, система А может иметь два равновероятных состояния: А1 и А2. Тогда полное выяснение состояния этой системы несет информацию один бит, и, значит, можно ее получить в результате ответа на один вопрос. Действительно, задав один-единственный вопрос: "Находится ли система в состоянии А1?" и получив на него ответ "да" или "нет", мы полностью выясним состояние системы. Энтропия обладает следующими свойствами: а) энтропия всегда неотрицательна, так как значения вероятностей выражаются величинами, не превосходящими единицу, а их логарифмы - отрицательными числами или нулем, так что члены суммы (2.7) неотрицательны; б) если pi = 1 (а все остальные pj = 0, j = 1, ..., (n-1)), то Н(А) = 0. Это тот случай, когда об опыте или величине все известно заранее и результат не дает новую информацию; в) H(A) = Hmax при p1 = p2 = ... = pn = 1 / n, при этом
г) энтропия системы, состоящей из двух подсистем А и В (состояния системы образуются совместной реализацией объектов А и В), то есть: Н(АВ) = Н(А) + Н(В). Если события равновероятны и статистически независимы, то оценки количества информации, по Хартли и Шеннону, совпадают. Это свидетельствует о полном использовании информационной емкости системы. В случае неравных вероятностей количество информации, по Шеннону, меньше информационной емкости системы. Количество информации тогда и только тогда равно энтропии, когда неопределенность ситуации снимается полностью. В общем случае нужно считать, что количество информации есть уменьшение энтропии вследствие опыта или какого-либо другого акта познания. Если неопределенность снимается полностью, то информация равна энтропии: I = H. В случае неполного разрешения имеет место частичная информация, являющаяся разностью между начальной (H0) и конечной (H1) энтропией: I = H0 - H1. Задача 1. Вероятность первого события составляет 0,5, а второго и третьего — 0,25. Какое количество информации мы получим после реализации одного из них? Решение. Р1=0,5; Р2=Р3=0,25 Þ Ответ: 1,5 бита. Задача 2. За контрольную работу по информатике получено 8 пятерок, 13 четверок, 6 троек и 2 двойки. Какое количество информации получил Васечкин при получении тетради с оценкой? Решение.
Ответ: 1,77 бит. Задача 3. Добрый экзаменатор никогда не ставит двоек по информатике. По причине своей доброты он заранее определил количество отметок каждого вида и произвольно расставил их абитуриентам. Количество информации, содержащееся в сообщении "Абитуриент Иванов не сдал экзамен на отлично", равно 3-log27 бит. Информационный объем сообщения "Абитуриент Сидоров получил четверку" равен двум битам. Определите информационный объем зрительного сообщения о полученной оценки абитуриентом Сидоровым. Решение. Из условия видно, что количество оценок, распределенных экзаменатором различное и вопрос задачи указывает на одну из всех возможных оценок, поэтому воспользуемся подходом к определению количества информации для неравновероятных событий, а именно формулой Шеннона. Обозначим i4 – количество информации в сообщении "Абитуриент Сидоров получил четверку", i4или3 – количество информации в сообщении "Абитуриент Иванов не сдал экзамен на отлично", I - информационный объем зрительного сообщения о полученной оценки абитуриентом Сидоровым, к – показатель определенной оценки, р3, р4, р5 – вероятности выставления троек, четверок и пятерок соответственно, р4или3 – вероятность выставления оценки не отлично
Ответ: 1,3 бит. Таковы в самых общих чертах принципиальные основы классической теории информации. Она дает полезный аппарат, позволяющий решать ряд важных практических задач (например в теории связи при кодировании речи или изображений). Однако этот аппарат не универсальный, и множество ситуаций не укладывается в шенноновскую модель. Отметим, что далеко не всегда можно заранее (до сообщения) установить перечень возможных состояний системы и вычислить их вероятности. Например, вряд ли можно численно оценить вероятность того, что в нашей солнечной системе существует еще одна - десятая - планета. Тем не менее, с точки зрения обычного здравого смысла (а не нарушать его - естественное требование к теории) ясно, что сообщение об открытии новой планеты должно нести очень большую информацию, но оценить ее в битах не удается. Другой пример. Допустим, что система радиолокационных станций ведет наблюдение за воздушным пространством с целью обнаружения самолета противника. Система А, за которой ведется наблюдение, может быть в одном из двух состояний:
Выяснение, в каком из них именно она находится, в рамках классической теории в лучшем случае принесло бы нам информацию один бит, равную информации о том, какой стороной вверх упала монета. Совершенно ясно, что по своей важности первое сообщение несравненно больше второго, но оценить его в рамках классической теории невозможно. Таким образом, основным недостатком классической теории информации, ограничивающим ее применение, является то, что она, занимаясь только формальной ("знаковой" или "буквенной") стороной сообщений, оставляет в стороне их ценность и важность, вообще - содержание. | |||||||||||||||||||||||||||||||

| Заполните таблицу:
Обсудите заполненную таблицу с другими студентами группы. Внесите в нее необходимые исправления и дополнения. | ||||||||||||||||||||||||||||||
Рассмотрите следующую ситуацию:
Имеется шахматная доска, на одну из клеток которой поставлена фигура (слон). Предположим, что все клетки выбираются с одинаковой вероятностью. Определим информацию, заключенную в сообщении о том, где стоит слон.
У системы А (слон) 64 равновероятных состояния; ее энтропия равна:
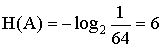 Значит, сообщение, полностью устраняющее неопределенность состояния системы (указание, где стоит слон), должно содержать ровно шесть битов информации. А из этого следует, что положение слона можно точно выяснить с помощью не более чем шести вопросов.
Попробуйте их сформулировать.
Значит, сообщение, полностью устраняющее неопределенность состояния системы (указание, где стоит слон), должно содержать ровно шесть битов информации. А из этого следует, что положение слона можно точно выяснить с помощью не более чем шести вопросов.
Попробуйте их сформулировать.
| |||||||||||||||||||||||||||||||

| Решите следующие задачи:
|
Модуль 3.
Системы счисления
Тема 3.1 Системы счисления. Представление чисел в различных системах счисления.
Основные понятия: позиционные и непозиционные системы счисления, алфавит, базис, основание системы счисления, порядок.
Условные обозначения:
 - задания до чтения текста - задания до чтения текста
|  - задания во время чтения - задания во время чтения
|  - задания после чтения - задания после чтения
|

| Используя данные ключевые слова, составьте рассказ из трех-четырех предложений. Ключевые слова: алфавит, цифра, позиция, запись, число. Познакомьтесь с рассказами других студентов вашей группы, сравните их: что в них общего и в чем различие? Придумайте название к вашим рассказам. |

| Прочитайте текст. Во время чтения делайте пометки на полях: «V» - уже знал; «+» - новая информация; «-» - думал иначе, «?» - не понятно, есть вопросы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Система счисления - совокупность приемов и правил для записи чисел цифровыми знаками. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая система счисления должна давать возможность представления любого числа в рассматриваемом диапазоне; это представление должно быть единственным, удобным для оперирования с ним.
Непозиционная система счисления - система, для которой значение символа не зависит от его положения в числе. Принципы построения таких систем не сложны. Для их образования используют в основном операции сложения и вычитания. Например, система с единым символом - палочкой - встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать количество палочек, равное данному числу. Эта система не эффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, X, V, L, C, D, M и т.д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числах LX и XL символ X принимает два различных значения : +10 - в первом случае и -10 - во втором.
Позиционная система счисления - система изображения чисел, в которой значение символа зависит от его позиции (местоположения) в числе.
В дальнейшем изложении будем рассматривать только позиционные системы.
Наибольшее распространение получила десятичная система счисления, в которой для записи чисел используются цифры 0, 1, ..., 9.
Самыми распространенными в вычислительной технике являются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.
Двоичная система наиболее применима в компьютерной технике. Ее преимущества:
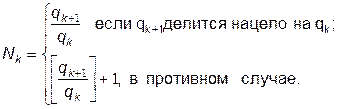 Пример 1.Приведем сводную таблицу, характеризующую некоторые позиционные системы счисления.
Пример 1.Приведем сводную таблицу, характеризующую некоторые позиционные системы счисления.
Основанием Р-ичной системы счисления может быть любое натуральное число, большее единицы. Системой счисления с минимальным основанием является двоичная система, все числа в которой записываются с помощью 0и 1. Пример 2.Приведем запись некоторых десятичных чисел в различных нетрадиционных позиционных системах счисления.
Мы видим, что для описания системы счисления используются понятия «базис», «алфавит», «основание». Для однозначного определения позиционной системы счисления, у которой в качестве цифр используются натуральные числа и 0, необходимо и достаточно указать только ее базис: последовательность чисел ..., qо, qv ..., qп, .... Все остальные компоненты системы являются производными от базиса. Последовательность чисел может являться базисом позиционной системы счисления только тогда, когда в соответствующей этому базису системе может быть представлено любое число (если система предназначена только для нумерации целых чисел, то любое целое число). В качестве цифр систем счисления могут быть использованы любые символы, это наглядно демонстрируют нам ученые, занимающиеся историей математики: вавилоняне использовали клиновидные цифры (у них не было бумаги, и «писали» они на мягких глиняных дощечках); китайцы использовали иероглифы; мы используем арабские цифры. Однако в математике придерживаются следующих договоренностей в отношении вида используемых цифр. Если основание системы счисления Р меньше 10, то для символьного представления цифр в ней, как правило, используются первые Р десятичных цифр (от 0 до Р - 1). Например, в пятеричной системе счисления будут использоваться пять цифр: 0, 1, 2, 3, 4. Для 10 < Р < 37 в качестве первых десяти цифр также обычно используют их десятичное представление, а для остальных цифр — буквы латинского алфавита. Для систем счисления с основаниями, большими 36, единых правил для формы записи цифр не существует. Для двоичной, восьмеричной, десятичной и шестнадцатеричной систем счисления приведем обозначения цифр:
Любое десятичное число можно представить в любой позиционной системе счисления, а для целых чисел в большинстве систем это можно сделать единственным способом. Пусть q — произвольное натуральное число, большее единицы. Существует и единственно представление любого натурального числа A в виде степенного ряда: Дата добавления: 2016-09-20; просмотров: 1582; |
Генерация страницы за: 0.023 сек.

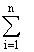
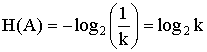
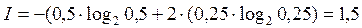 бита.
бита.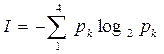 , рк=
, рк= 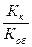 .
.
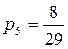 ,
, 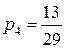 ,
, 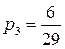 ,
, 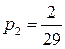 Подставляем полученные вероятности:
Подставляем полученные вероятности:
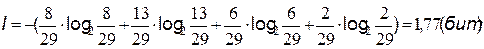
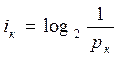 ,
, 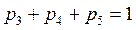 , рк=
, рк= 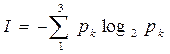 .
Найдем вероятности р5 и р4:
3-log27=
.
Найдем вероятности р5 и р4:
3-log27= 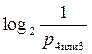 Þ
Þ 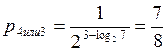 Þ Þ
Þ Þ 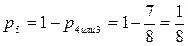 ,
аналогично
,
аналогично 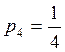 Þ
Þ 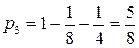 .
Подставляем полученные вероятности в формулу (*)
.
Подставляем полученные вероятности в формулу (*)