ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ
Пусть дана возрастающая или убывающая функция 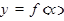 , т. е. между переменными
, т. е. между переменными 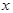 и
и 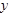 устанавливается взаимно однозначное соответствие. Рассматривая эти значения
устанавливается взаимно однозначное соответствие. Рассматривая эти значения 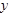 как значения аргумента, а
как значения аргумента, а 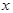 как значения функции, получим
как значения функции, получим 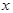 как функцию от
как функцию от 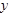 :
:
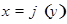 .
.
Эта функция называется обратной для функции 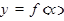 . Очевидно, что и функция
. Очевидно, что и функция 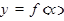 является обратной для функции
является обратной для функции 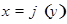 .
.
Теорема. Если для функции 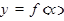 существует обратная функция
существует обратная функция 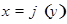 , которая рассмаириваемой точке
, которая рассмаириваемой точке 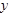 имеет производную
имеет производную 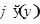 , отличную от нуля, то в соответствующей точке
, отличную от нуля, то в соответствующей точке 
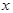 функция
функция 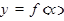 имеет производную
имеет производную 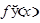 равную
равную 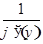 т.е. справедлива формула
т.е. справедлива формула
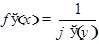 . (*)
. (*)
Доказательство. Дифференцируя обу части равенства 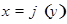 по
по 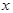 , считая
, считая 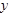 функцией от
функцией от 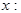
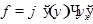 Откуда
Откуда 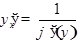 . Учитывая, что
. Учитывая, что 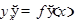 , получаем формулу (*), которую можно записать в виде
, получаем формулу (*), которую можно записать в виде
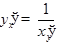 (**)
(**)
Легко выяснить ее геометрический смысл. Мы знаем что, производная 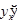 есть тангенс угла
есть тангенс угла 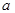 , образованного касательной к графику функции
, образованного касательной к графику функции
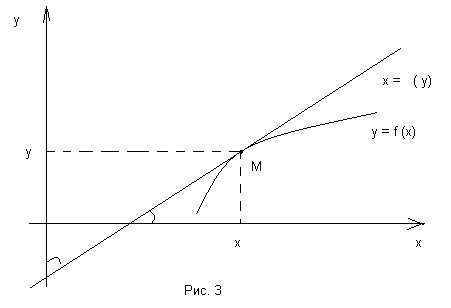
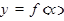 с осью
с осью 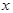 . Но обратная функция
. Но обратная функция 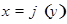 имеет тот же график, лишь независимая переменная для нее откладывается по оси
имеет тот же график, лишь независимая переменная для нее откладывается по оси 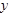 . Поэтому производная
. Поэтому производная 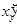 равна тангенсу угла
равна тангенсу угла 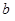 , составленной той же касательной с осью
, составленной той же касательной с осью 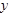 . Таким образом выведенная формула сводится к известному соотношению
. Таким образом выведенная формула сводится к известному соотношению 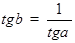 , связывающему тангенсы двух углов
, связывающему тангенсы двух углов 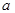 и
и 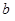 , сумма которых равна
, сумма которых равна 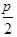 .
.
 Обратные тригонометрические функции
Обратные тригонометрические функции
Рассмотрим функцию 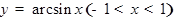 , причём
, причём 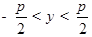 . Она является обратной для функции
. Она является обратной для функции 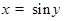 , имеющей положительную производную
, имеющей положительную производную 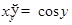 . В таком случае существует также производная
. В таком случае существует также производная 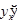 и равна по нашей формуле
и равна по нашей формуле
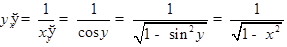 ;
;
корень берём со знаком «плюс», так как 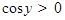 .
.
Значения 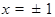 мы исключили, ибо для соответствующих значений
мы исключили, ибо для соответствующих значений 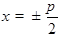 производная
производная 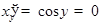 .
.
Функция 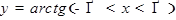 служит обратной для функции
служит обратной для функции 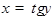 .
.
По нашей формуле 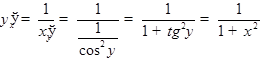 . Аналогично можно получить:
. Аналогично можно получить:
для 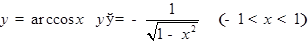 ,
,
для 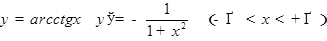 .
.
Примеры. 1) 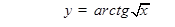
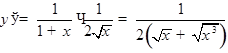
2) 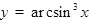 .
.
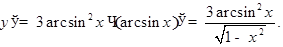
3) 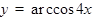
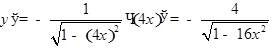 .
.
4) 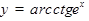 .
.
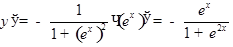 .
.
ТАБЛИЦА ПРОИЗВОДНЫХ
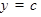
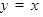
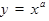
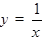
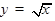
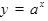
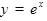
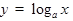
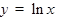
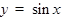
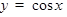
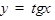
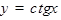
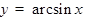
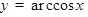
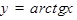
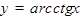
| 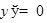
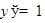
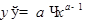
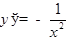
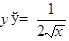
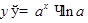
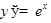
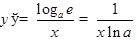
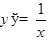
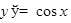
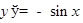
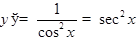
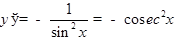
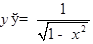
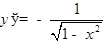
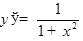
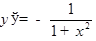
|
Дата добавления: 2016-09-20; просмотров: 486;
