ПРОСТЕЙШИЕ ПРАВИЛА ВЫЧИСЛЕНИЯ
ПРОИЗВОДНЫХ
 Постоянный множитель можно вынести за знак производной
Постоянный множитель можно вынести за знак производной 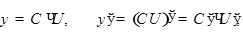 где
где 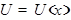
Докозательство: Дадим независимой переменной 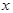 приращение
приращение 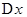 , тогда функция получит приращение
, тогда функция получит приращение 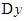 равное
равное
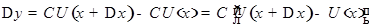 .
.
Разделим обе части равенства на 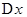 и перейдем к пределу при
и перейдем к пределу при 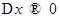 .
.
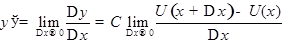 т.е.
т.е. 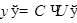 .
.
Пример. 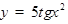
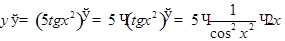
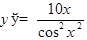
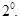 Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций.
Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций.
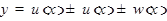
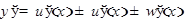
Доказательство. Дадим переменной 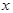 приращение
приращение 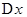 . Для значения аргумента
. Для значения аргумента 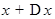 имеем
имеем 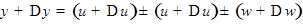 , где
, где 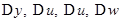 - приращения функций
- приращения функций 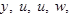 соответствующие приращению
соответствующие приращению 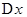 . Отсюда
. Отсюда 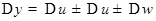 .
.
Разделим на 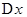
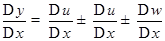 . Следовательно,
. Следовательно, 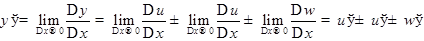
Или окончательно
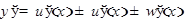
Пример. 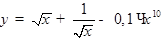 ,
,
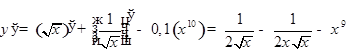 .
.
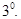 производная двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй функции, т.е.
производная двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй функции, т.е.
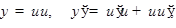 где
где 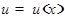 и
и 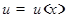
Доказательство. Приращение аргумента 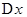 соответствуют приращения
соответствуют приращения 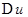 ,
, 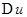 и
и 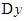 . При этом
. При этом
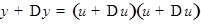 и
и
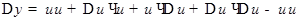 ,
,
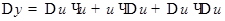 ,
,
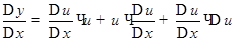
Так как при 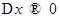 и
и 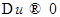 , то
, то 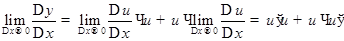 , т.е. существует производная
, т.е. существует производная 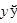 и равна
и равна
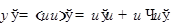
Если 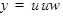 , при чём
, при чём 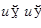 и
и 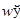 существуют, то
существуют, то
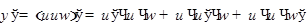
Примеры: а) 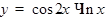
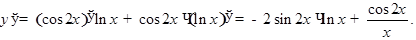
б) 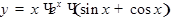
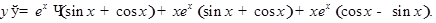
 . Производная дроби (частного от деления двух функций) равна дроби, числитель которой равен разности производной между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, а знаменатель есть квадрат знаменателя данной дроби.
. Производная дроби (частного от деления двух функций) равна дроби, числитель которой равен разности производной между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, а знаменатель есть квадрат знаменателя данной дроби.
Поизводная дроби (частного от деления двух функций) равна производной числителя, умноженной на знаменатель, минус числитель, умноженный на производную знаменателя, и деленное все на квадрат знаменателя, т.е.
если 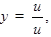 то
то 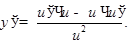
Доказательство. Если 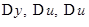 суть приращения функций
суть приращения функций 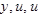 соответствующие приращению
соответствующие приращению 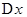 аргумента
аргумента 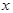 , то
, то 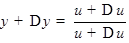 ,
,
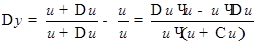 ,
,
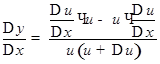 .
.
Устремляя 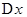 к нулю (причем одновремеено и
к нулю (причем одновремеено и 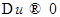 ), получим,
), получим,
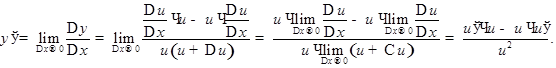
Примеры: а) 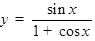
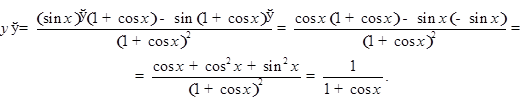
б) 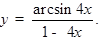
Дата добавления: 2016-09-20; просмотров: 440;
