ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

ПРОИЗВОДНАЯ И ЕЁ ВЫЧИСЛЕНИЕ

Задача о вычислении скорости движения точки. Рассмотрим свободное падение (в пустате) материальной точки. Пусть пройденный от начала падения путь S за время t выразится по формуле 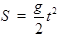(1)

О

где 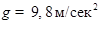. Поставим задачу: определить

скорость 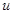движения точки в момент 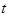, когда она

S находится в положении М (Рис. 1)

Придадим переменной t приращение 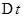, и в

M момент 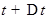точка будет в положении .

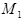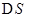Приращение 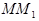пути за промежуток времени

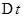обозначим через 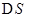. Подставляя в (1)

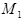
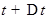вместо t, получим для нового значения пути

выражение

,

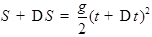откуда

Рис. 1 .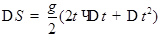

Разделив 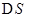на 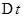, получим среднюю скорость падения точки на участке :

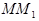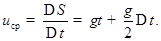
Скоростью 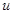точки в момент времени t называют предел, к которому стремится средняя скорость 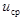за промежуток 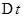, когда 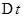стремится к 0.

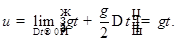
Аналогично вычисляется скорость 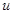и в общем случае прямолинейного движения точки.

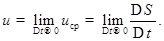
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть функция 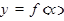определена в некотором промежутке x. Дадим аргументу x некоторое приращение 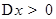, не выходящие из промежутка х. Тогда при значении аргумента 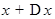будем иметь 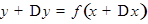. Следовательно, приращение функции 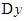равно

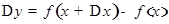
Предел отношения приращения функции 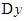к приращению независимой переменной 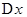при стремлении 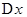к 0, т.е.

,

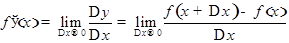называется производной функции 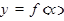по независимой переменной x.

Наряду с обозначением 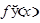для производной употребляются и другие обозначения, например

.

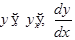Конкретное значение производной при 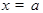обозначается 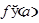или 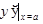.Действие нахождения производной от функции 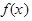называется дифференцированием этой функции.

Пользуясь введённым понятием производной о скорости движения точки можно сказать следующее:

Скорость 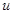есть производная от производного пути S по переменной t.