ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть задана сложная функция 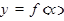 , т.е. такая, что её можно представить в следующем виде:
, т.е. такая, что её можно представить в следующем виде: 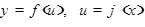 или
или 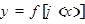 . В выражении
. В выражении 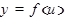 переменную и называют промежуточным аргументом. Правило дифференцирования сложной функции сложной функции можно сформулировать в виде теоремы:
переменную и называют промежуточным аргументом. Правило дифференцирования сложной функции сложной функции можно сформулировать в виде теоремы:
Пусть 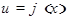 имеет в некоторой точке
имеет в некоторой точке 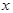 производную
производную 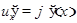 , а qфункция
, а qфункция 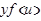 имеет в соответствующей точке
имеет в соответствующей точке 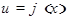 производную
производную 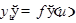 . Тогда сложная функция
. Тогда сложная функция 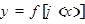 в точке
в точке 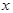 также будет иметь производную, равную произведению производных функций
также будет иметь производную, равную произведению производных функций 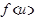 и
и 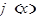 :
: 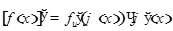 , или короче
, или короче 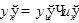 .
.
Доказательство. Дадим переменной 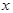 произвольное приращение
произвольное приращение 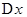 , которому соответствует приращение
, которому соответствует приращение 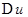 , а приращение
, а приращение 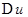 соответствует приращение
соответствует приращение 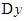 . Причём при
. Причём при 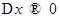 будет
будет 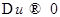 и
и 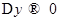 .
.
По условию теоремы 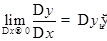 , а поэтому, пользуясь определение предела, можем записать (при
, а поэтому, пользуясь определение предела, можем записать (при 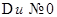 ):
): 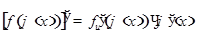 , или короче
, или короче 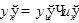 .
.
Доказательство. Дадим переменной x произвольное приращение 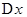 , которому соответствует приращение
, которому соответствует приращение 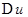 , а приращение
, а приращение 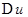 соответствует приращению
соответствует приращению 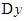 . Причем при
. Причем при 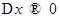 будет
будет 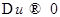 и
и 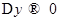 .
.
По условию теоремы 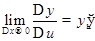 , а поэтому, пользуясь определением предела, можем записать (при
, а поэтому, пользуясь определением предела, можем записать (при 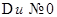 ):
):
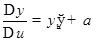 , (1)
, (1)
где 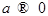 при
при 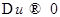 .
.
Перепишем равенство (1) в виде
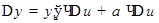 (2)
(2)
Это равенство справедливо и при 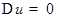 при произвольном
при произвольном 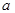 . Разделив его почленно на
. Разделив его почленно на 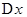 , получим
, получим
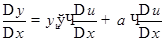 .
.
При 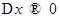 к нулю будет стремится и
к нулю будет стремится и 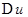
 , а также зависящие от
, а также зависящие от 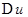 величина
величина 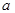 . Следовательно, существует предел
. Следовательно, существует предел
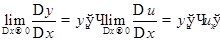 , который и представляет собою искомую производную
, который и представляет собою искомую производную 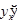 .
.
Примеры. 1) Пусть 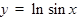 , иначе говоря,
, иначе говоря, 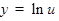 , где
, где 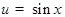 . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции 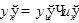 будем иметь
будем иметь 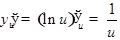 при
при 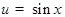 . Таким образом
. Таким образом 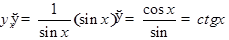 .
.
2) 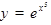 , т.е.
, т.е. 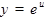 , где
, где 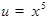 ;
;
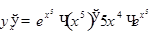 .
.
3) 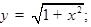 т.е.
т.е. 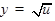 , где
, где 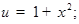
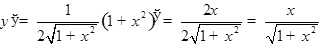 .
.
4) 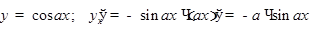
5) 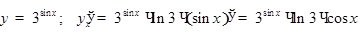 .
.
6) 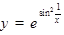 ; в этом случае
; в этом случае
Дата добавления: 2016-09-20; просмотров: 396;
