Ускладнення у визначенні областей переважання

Якщо послідовність усіх N ступінчатих констант спадна,

K₁ > K₂ > . . . > K_N,

то у всіх N+1 реаґентів існують області переважання, з межами pL = lg K_i. Якщо ж K_i < K_i+1 (аномальна послідовність), то ML_i не має області переважання. Якщо сусідніми є області переважання ML_i і ML_i+j (j > 1), то

ML_i + j L D ML_i+j,

lg K = lg b_i+j – lg b_i = lg K_i+1 + lg K_i+2 + . . . + lg K_i+j, (lg b₀ = 0),

і, згідно ЗДМ,

lg ([ML_i+j] / [ML_i]) = lg K – j pL.

Межа областей переважання, [ML_i+j] = [ML_i] при pL = (lg K) / j, середньому від логарифмів констант.

Розглянемо приклад – комплекси Ag⁺ із NH₃. Тут lg K₁ = 3,31, lg K₂ = 3,91, отже послідовність констант є аномальною, K₁ < K₂. На допоміжній смузі схеми косим штрихом (\\\ або ///) позначено області, де над AgNH₃⁺ переважають інші комплекси. Згідно ЗДМ, [AgNH₃⁺] < [Ag⁺] при pNH₃ > lg K₁ = 3,31; [AgNH₃⁺] < [Ag(NH₃)₂⁺] при pNH₃ < lg K₂ = 3,91. Ці області перекриваються,

Отже, у проміжному комплексі AgNH₃⁺ немає області переважання. Реагенти з областями переважання взаємно перетворюються за реакцією

Ag⁺ + 2NH₃ D Ag(NH₃)₂⁺, lg b₂ = lg K₁ + lg K₂ = 7,22.

Для [Ag⁺] = [Ag(NH₃)₂⁺], як частинний випадок загальної умови, маємо межу областей, pNH₃ = (lg b₂) / 2 = 3,61.

Алґоритм побудови областей переважання:

1. Знайти межу областей переважання. Для спадної послідовності ступінчатих констант стійкості межі областей дорівнюють lg K_i. Якщо таку послідовність порушено (вона є аномальною), то проміжні комплекси ніде не переважають. Межі комплексів, найближчих за складом до ніде не переважаючих, дорівнюють середньому арифметичному логарифмів констант аномальної послідовності.

2. До комплексу МL_і із найменшим числом координованих ліґандів L (і = 0 для вільного М) віднести праву область на осі рL; комплексам із зростаючим числом координованих ліґандів - області, що послідовно розташовані cправа наліво; пропускаємо комплекси, що ніде не переважають.

КЛД для систем із одноядерними комплексами.Для гомоґенних реакцій, змінюючи головну змінну pX = pL (або pH чи pe), міняємо дві залежних змінних – логарифми рівноважних концентрацій двох реагентів, і рівняння прямої вже несправедливе. Наближену асимптоту маємо, приймаючи, що майже весь M перетворився у переважаючий продукт ML_i, і одна із залежних змінних є майже постійною, lg [ML_і] » lg t(M), де t(M) − загальна концентрація компоненту M. Ґрафік іншої змінної стає лінійним. Наближення тим краще, чим глибше ми у області переважання ML_і. У областях для різних ML_і асимптоти різні, й наближений ґрафік - ламана.

Розглянемо приклад – кислотно-основні перетворення ацетату, t(HAc) = t = 0,10 моль/л. HAc переважає, якщо pH < lg K_Н = 4,76. Для [HAc] » t(Ac^‑) = t наближеним ґрафіком є lg [HAc] » lg t, горизонтальний промінь від (-¥) до так званої точки системи (ТС), із абсцисою lg K_Н. Правіше за неї переважає Ac^-, [Ac^‑] » t = 0,10 моль/л, і, згідно ЗДМ

lg [HAc] = lg K_Н + lg [Ac^-] – pH » lg K_Н + lg t – pH,

асимптота, промінь униз під кутом 45 ^о (танґенс ‑1) із ТС – кінця горизонтальної асимптоти. Підставляючи pH = lg K_Н у рівняння для lg [HAc], одержуємо lg t. Значить, й ця гілка наближеного ґрафіка йде через ТС.

Алґоритм побудови КЛД для систем із одноядерними продуктами. У простих випадках не записуємо реакцій та ЗДМ. Танґенс кута нахилу є різницею стехіометричних індексів при X у формулах частинок – тієї, що відповідає ґрафіку, й переважаючої у відповідній області.

Так, для lg [HAc] у області переважання HAc лінія горизонтальна, а у області переважання Ac^- танґенс за абсолютною величиною дорівнює 1 (формули Ac^- і HAc відрізняються на 1 H⁺). Знак танґенса такий, що lg [HAc] зменшується, віддаляючись від області переважання HAc: графік не перевищує горизонтальної асимптоти – максимуму функцій! Зломи замінюють плавними спряженнями. На межі областей, де найбільше порушуються наближення lg [HAc] » lg t або lg [Ac^‑] » lg t, речовину з загальною концентрацією t поділено навпіл між НАс та продуктом Ac^‑,

[HAc] = [Ac^‑] = t / 2, lg [HAc] = lg [Ac^-] = lg t – lg 2,

і згладжені ґрафіки перетинаються нижче за ТС на lg 2 » 0,3. Для lg [Ac^-] наближений ґрафік – ламана, що складена з асимптот – від ТС до ¥ (горизонтальної) і від – ¥ до ТС (з танґенсом кута нахилу 1).

КЛД, рис. 3, доповнено графіками lg [H⁺] і lg [OH^-]. Пряма lg [H⁺] йде через початок координат, а lg [OH^‑] – через точку (pH = ‑lg K_w, 0). Танґенси їх кутів нахилу відповідно дорівнюють (‑1) й 1.

Там, де більше двох областей переважання, для кожної – інше наближене рівняння, пов’язане з ЗДМ реакції перетворення переважаючого реагенту (скажімо, ML_і), у той, ґрафік якого досліджуємо (скажімо ML_k),

ML_i + (k - i) L D ML_k, lg b_k – lg b_i.

lg [ML_k] = (lg b_k – lg b_i) + lg [ML_i] + (i – k) pL »

» (lg b_k – lg b_i) + lg t(M) + (i – k) pL .

Щоб координати точок перетину відрізків не знаходити з рівнянь, зауважимо, що функція неперервна, а ґрафік наближеної функції – ламана зі зломами на межах областей переважання. Графік почнемо із горизонтального відрізка між ТС і продовжимо похилими відрізками в інші області переважання. Отже, алґоритм побудови КЛД:

Обчислити значення головної змінної pL на межах областей переважання окремих частинок.

Нанести на діаґраму точки системи (ТС) з абсцисами, що обчислені на кроці 1, і ординатою lg t(M).

Почати наближений ґрафік lg [ML_k] із відрізка, кінці якого у ТС на межах області переважання ML_k, а для частинки, що не має області переважання – у ТС на межах областей переважання частинок, найближчих за складом до розгляданої.

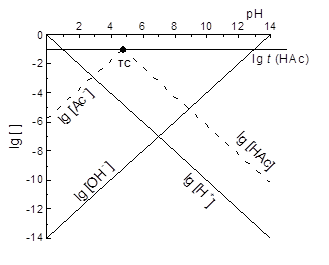
	a
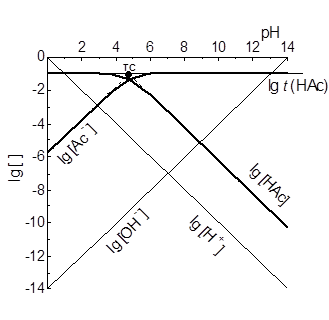
	b

Рис. 3. КЛД для кислотно-основних перетворень ацетату, t(HAc) = t = 0,10 моль/л: (а) ескіз перед побудовою спряжень; (б) КЛД.

Продовжити ґрафік lg [ML_k] ламаною у область переважання ML_і. Танґенс кута нахилу відрізків ламаної дорівнює (i – k), різниці стехіометричних індексів при L для частинки ML_і, що переважає у відповідній області, та ML_k. Кінці відрізка – на межах областей (під ТС).

Якщо точність ґрафіків у околі ТС недостатня для аналізованої проблеми, то замінити зломи плавними спряженнями, точка перетину яких відхиляється на D = ‑ lg j за ординатою від зламу, де j – число сортів частинок, концентрації яких великі й майже рівні у ТС.

Алґоритм зручніший, ніж для гетероґенних систем. Лише за ступінчатими константами відтворюємо (навіть в уяві!) ґрафіки для найбільших концентрацій – горизонтальні відрізки та похилі, що безпосередньо від них відходять.

Щоб вирішити більшість проблем, потрібно розглядати лише декілька найбільших концентрацій, інформація про які міститься у верхній частині КДД, а подробиці поведінки ґрафіків біля ТС неістотні. Часто достатньо горизонтальних і перших похилих відрізків, без 5-го кроку.

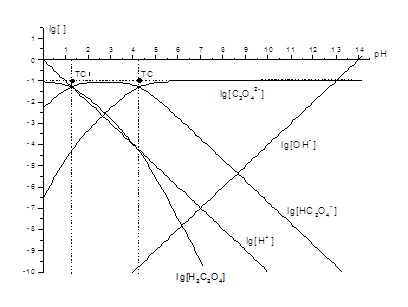
Рис. 4. КЛД для кислотно-основних перетворень оксалату, t(H₂С₂О₄) = t = 0,10 моль/л.

Розглянемо КЛД для Н₂С₂О₄, t(Н₂С₂О₄) = t = 0,10 моль/л, головна змінна pH. Для продуктів приєднання іону Н⁺ до іона С₂О₄^2‑: lg K_H1 = 4,266, lg K_H2 = 1,256 [I = 0]. Це рН на межах областей переважання (крок 1). На кроці 2 наносимо ТС із координатами (1,3, ‑1) та (4,3, ‑1), ордината lg t = ‑1. На кроці 3 будуємо наближені ґрафіки. Ґрафік lg [Н₂С₂О₄] починаємо з горизонтального променя на висоті –1, від ‑ ¥ до лівої ТС, ґрафік lg [НС₂О₄^‑] – із відрізка між обома ТС, а lg [С₂О₄^2‑] – із променя від правої ТС на + ¥. На кроці 4 ґрафік lg [Н₂С₂О₄] продовжуємо праворуч (де переважає іон НС₂О₄^‑, що відрізняється від Н₂С₂О₄ на іон Н⁺) відрізком із танґенсом кута нахилу (‑1). Напрям ухилу є очевидним, бо ґрафік порівняно з горизонтальним відрізком може лише спадати. Після правої ТС, де переважає С₂О₄^2‑, ґрафік продовжуємо променем із танґенсом кута нахилу (‑2). Аналоґічно будуємо похилі ділянки ґрафіків lg [НС₂О₄^‑] та lg [С₂О₄^2‑], тільки тут вже наявні ділянки зростання функцій. На кроці 5 спрягаємо всі зломи (рис. 4).

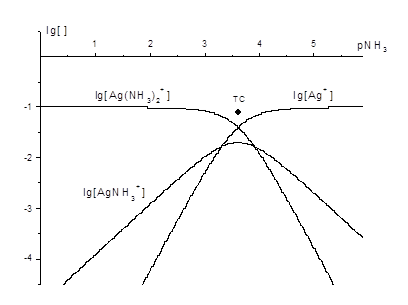
Рис. 5. КЛД для комплексів Ag⁺ із NH₃, головна змінна pNH₃, t(Ag⁺) = t = 0,10 моль/л.

На КЛД для t(Ag⁺) = t = 0,10 моль/л, головна змінна pNH₃, області переважання мають Ag⁺ та Ag(NH₃)₂⁺. Горизонтальні відрізки наближених ґрафіків lg [Ag⁺] та lg [Ag(NH₃)₂⁺] переходять у похилі з танґенсами ± 2, бо переважаючі комплекси, відокремлені межею, pNH₃ = (lg b₂) / 2 = 3,61, відрізняються на 2 ліґанди NH₃. Асимптоти перетинають горизонтальну лінію lg [] = lg t у точках із абсцисами – логарифмами ступінчатих констант. Для AgNH₃⁺ ці точки не співпадають з ТС. Приймимо

lg K₁ » lg K₂ » (lg b₂) / 2,

бо ступінчаті константи дуже близькі, й проведемо асимптоти графіка lg [AgNH₃⁺] через ту саму ТС двома променями з танґенсами ± 1. У ТС

lg [Ag⁺] = lg [Ag(NH₃)₂⁺] » lg [AgNH₃⁺] » lg (t / 3) = ‑ 1,5

й спряження проводимо на lg 3 » 0,5 нижче за ТС.