Лінійні комбінації реакцій
Ми вже мали змогу звернути увагу, що рівняння приєднання кількох протонів до багатозарядного аніону (або кількох лігандів до іону-комплексоутворювача) характеризуються загальною константою, яка дорівнює добутку ступінчастих констант: βn = K·K·…·Kn.
Аналогічним чином можна обчислитити константу більш складної рівноваги, використовючи константи простих рівноваг.
Приклад 1. Розглянемо рівновагу розчинення малорозчинної солі слабої кислоти в розчині сильної кислоти.
CaCO3↓ + 2H+ D Ca2+ + H2O + CO2; K-?
Розв’язання. Реакція складається з двох простих рівноваг:
CaCO3↓ DCa2+ +CO32- ; Ks=10‑8,52
CO32- +2H+DH2O+CO2; βH2=KH1·KH2=1010,33· 106,35=1016,68
Значить константа рівноваги вихідної реакції:
K= Ks βH2=10‑8,52 ·1016,68=108,16;
Відповідь: K=1,45·108.
Приклад 2. Рівновага розчинення малорозчинного гідроксиду в розчині аміаку:
Cu(OH)2↓ +4NH3 DCu(NH3)42++2OH- K=?
Розв’язання. Вихідною речовиною є осад гидроксиду, значить першою рівновагою слід розглянути рівновагу розчинення:
Cu(OH)2↓D Cu2++2OH Ks = 10-19,32.
Іони Cu2+, що утворилися, взаємодіють із молекулами аміаку:
Cu2+ + 4NH3 D Cu(NH3)42+ β4 =1011,75.
константа рівнваги вихідної реакції:
K = Ks·β4=10-19,32·1011,75 = 10-7,57.
Відповідь: K = 2,69·10-8.
Приклад 3. Рівновага утворення осаду при руйнуванні комплексної сполуки
BiI4-+PO43- D BiPO4↓ + 4I-.
Розв’язання. Вихідними є комплексні аніони, значить першою рівновагою слід розглянути рівновагу дисоціації:
BiI4- D Bі3+ + 4I- β4-1 = 10-15.
Іони Bі3+, що утворилися, взаємодіють із аніонами фосфату
Bі3+ + PO43- D BiPO4↓ Ks-1 = 1022.
константа рівнваги вихідної реакції:
K= β4-1· Ks-1 =10-15·1022,9 = 107,9;
Відповідь: K = 7,94·107.
Теоретично вивчаючи рівноважні системи, враховуємо ЗДМ для різних реакцій. Замість того, щоб перетворювати алґебраїчні рівняння ЗДМ, наочніше перетворити реакції, для яких є довідкові дані, переходячи до лінійних комбінацій реакцій.
Розглянемо вихідні реакції
0 D S aij Aj, (16)
де i – номер реакції, aij – стехіометричний коефіцієнт у i-й реакції при реагенті Aj . Множачи реакції на множники ki й додаючи добутки, утворюємо лінійну комбінацію
0 D S (S ki aij) Aj, (17)
із стехіометричними коефіцієнтами – лінійними комбінаціями коефіцієнтів вихідних реакцій.
Логарифмуючи рівняння ЗДМ для реакції (7), маємо
S aij lg aj = lg Ki,
де Kі – константа ЗДМ для і-ї реакції; aj – активність реагенту Aj. Створюючи лінійну комбінацію цих рівнянь, маємо
(S ki aij) lg aj = S lg Ki = lg K, (18)
де K – константа ЗДМ лінійної комбінації (тобто реакції 8). Не ускладнюючи рівнянь ЗДМ, ki вибираємо так, щоб коефіцієнти (S ki aij) при деяких реагентах обертались на 0 (реагенти «скорочувались»), і відповідна активність у ЗДМ не входила. Комбінуючи n реакцій, «скорочуємо» принаймні (n - 1) реагентів. Лінійна комбінація задовольняє вимозі, що число атомів кожного елемента у реакції зберігається, бо їй задовольняють вихідні реакції.
Лінійно незалежні реакції – такі, що жодна з них не є лінійною комбінацією інших. Математичні терміни «лінійна комбінація» та «лінійна незалежність» відповідають структурі множини реагентів та реакцій. ЗДМ для незалежних реакцій є незалежними алґебраїчними рівняннями. Залежним реакціям відповідають залежні рівняння ЗДМ.
Розглянемо найчастіше вживані лінійні комбінації. Найпростіша з них – зворотна реакція, комбінація з однієї реакції, із множником (‑1). Наприклад, для щавлевої (оксалатної) кислоти маємо
H+ + C2O42‑ D HC2O4‑, lg KH1 = 4,266,
H+ + HC2O4‑ D H2C2O4, lg KH2 = 1,252.
Реакції кислотної дисоціації – зворотні до наведених:
H2C2O4 D H+ + HC2O4‑, lg Kа1 = ‑ lg KH2 = ‑ 1,252,
HC2O4‑ D H+ + C2O42‑, lg Kа2 = ‑ lg KH1 = ‑4,266.
Нумерація констант також обернена. Для констант стійкості її починають від основи Бренстеда, C2O42‑, другий індекс при lg KH і відповідає номерові іону Н+, що приєднується до C2O42‑. Для констант кислотої дисоціації її починають від H2C2O4, другий індекс при lg Kаі відповідає номерові іону Н+, що відщеплюється від Н2C2O4. Перехід від лоґарифму константи одного типу до іншого – це просто зміна знаку (множення на –1, той самий множник, на який множимо реакцію). Це випливає з рівнянь ЗДМ. Так,
lg a(HC2O4‑) ‑ lg a(H+) ‑ lg a(C2O42‑)} = lg KH2,
lg a(H+) + lg a(C2O42‑) ‑ lg a(HC2O4‑) = lg Ka1 = ‑ lg KH2.
Другий типовий випадок – перехід між загальними та ступінчатими константами. Так, для Zn2+ та NH3 маємо
| Zn2+ + 3 NH3 | D | Zn(NH3)32+, | lg b3 = 6,86, | |
| ‑1 | Zn2+ + 2 NH3 | D | Zn(NH3)22+, | lg b2 = 4,50, |
| Zn(NH3)22+ + NH33 | D | Zn(NH3)32+, | lg K3 = lg b3 –lg b2 = 2,36. |
Тут реакції подано «у стовпчик», ліворуч – множники ki. Радимо користуватися подібною наочною формою запису.
Простота переходу до константи зворотної реакції веде до зручнішого запису розглянутої лінійної комбінації:
| Zn2+ + 3 NH3 | D | Zn(NH3)32+, | lg b3 = 6,86, | |
| Zn(NH3)22+ | D | Zn2+ + 2 NH3 | ‑ lg b2 = ‑4,50, | |
| Zn(NH3)22+ + NH3 | D | Zn(NH3)32+, | lg K3 = lg b3 + lg b2 = 2,36. |
Із ЗДМ випливає перехід до константи лінійної комбінації,
lg a(Zn(NH3)32+) – lg a(Zn2+) – 3 lg a(NH3) = lg b3,
lg a(Zn(NH3)22+) – lg a(Zn2+) – 2 lg a(NH3)} = lg b2,
lg a(Zn(NH3)32+)–lg a(Zn(NH3)22+) – 3 lg a(NH3)3} = lg K3 = lg b3–lg b2.
Легко узагальнити цей результат,
lg Kі = lg bі ‑ lg b(і – 1), lg bі = 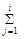 lg Kj .
lg Kj .
Наведемо ще приклади. Для реакції з участю іона металу Zn2+ маємо
Zn2+ + і Н2О D Zn(ОН)і2 ‑ i + і Н+, lg *bі = lg bі + і lg Kw,
де bі – загальна константа стійкості гідроксокомплексу,
Zn2+ + і ОН‑ D Zn(ОН)і2 ‑ i, lg bі ,
а Kw – константа автопротолізу води.
Для реакції твердої фази з утворенням комплексів власного аніону, наприклад, Hg2+ із I‑, маємо
HgI2(s) + (i – 2) I‑ D HgIi2 – i, lg Ksi = lg Ks0 + lg bi,
де Ks0 – добуток розчинності HgI2(s),
HgI2(s) D Hg2+ + 2 I‑, lg Ks0 = ‑24,07 [I = 0,5],
bi – загальна константа стійкості продукту – іодидного комплексу меркурію,
Hg2+ + i I‑ D HgIi2 ‑ i,
lg bi = 12,87 (i = 1); 23,82 (i = 2); 27,6 (i = 3); 29,8 (i = 4) [I = 0,5].
При i = 1 стехіометричний коефіцієнт (i – 2) є від’ємним, але ми вже звикли ставитись до реагентів так, як і до членів алґебраїчних рівнянь, переносячи їх із однієї частини рівняння в іншу зі зворотним знаком. Коефіцієнт (‑1) зліва означає, що відповідний реагент є продуктом реакції. Наведемо запис у стовпчик для реакцій, продуктом яких є останній комплекс,
| HgI2(s) | D | Hg2+ +2I- | lg Ks0 = -27,95, | |
| Hg2+ + 4 I‑ | D | HgI42‑ | lg b4 = 20,9, | |
| HgI2(s) + 2 I‑ | D | HgI42‑, | lg Ks4 = -7,05. |
Заощаджуючи обсяг довідників, не наводять реакцій, що безпосередньо відображають конкуренцію між різними ліґандами за комплексоутворювач, або між різними комплексоутворювачами за ліґанд. Безліч таких комбінацій можна скласти з наявних реакцій, вивчаючи, наприклад, маскування. З подібною проблемою ми зустрічаємось, вивчаючи обмін не ліґандами, а електронами, у окисно-відновних реакціях. У довідковій літературі звичайно подають відомості про умови рівноваги для так званих напівреакцій, за участю окисненої та відновленої форм і вільних електронів
nOx Ox + ne e- D nRed Red, (19)
n із відповідними індексами – стехіометричні коефіцієнти. Звичайно, інші учасники реакції крім Ox та Red також мають входити у рівняння (10).
Вільних електронів у водяних розчинах немає, отже, якщо якийсь реаґент здатен віддати електрони, то це має значення лише тоді, коли в системі є реагенти, що можуть ці електрони зв’язати.У теоретичних дослідженнях часто вживають лінійні комбінації двох різних напівреакцій, із яких вилучають електрони. Щоб обчислити константи ЗДМ таких комбінацій, потрібні константи для напівреакцій, що пов’язані з E0 – стандартними окисними (або окисно-відновними) потенціалами напівреакцій,
lg K = ‑ne k E0. (20)
Формою ЗДМ для напівреакції є рівняння Нернста,
E = E0 − (k E0/ne) (nRed lg aRed − nOx lg aOx), (21)
k = F / (2,3 RT),
де E – окисний потенціал, k – множник Нернста, F – постійна Фарадея, R – газова постійна, T – абсолютна температура, пов’язує потенціал напівреакції з логарифмом її константи. При 273,15 К (25 оС) коефіцієнт k дорівнює 0,0591 В. Окисний потенціал відповідає логарифмові активності електрона
lg ae = ‑ E / k. (22)
Чим потенціал більший, тим більша здатність форми Ox виступати як окисник. Щоб обчислити логарифм лінійної комбінації напівреакцій, логарифми констант напівреакцій зручніші за потенціали. Якщо реакцію (10) поділити на стехіометричний коефіцієнт при електроні, ne,
(nOx / ne) Ox + e‑ D (nRed / ne) Red,
у ній братимуть участь (nOx / ne) Ox та (nRed / ne) Red, еквіваленти окисненої і відновленої форми. Множник при E0 у формулі (11) відсутній.
Як приклад, розглянемо дію H5IO6 на Mn2+. Відомі напівреакції
MnO4‑ + 8 H+ + 5 e‑ D Mn2+ + 4 H2O, 127,5,
H5IO6 + H+ + 2e‑ D IO3‑ + 3 H2O, 54,0.
Запишемо першу у зворотному напрямі, щоб не вживати від’ємних коефіцієнтів,
| Mn2+ + 4 H2O | D | MnO4‑ + 8 H+ + 5 e‑, | ‑ 127,5, | |
| H5IO6 + H+ + 2e‑ | D | IO3‑ + 3 H2O, | 54,0, | |
| 2 Mn2+ + 5 H5IO6 | D | 2 MnO4‑ + 5 IO3‑ + 11 H+ + 7 H2O, |
lg K = 2×(‑127,5) + 5×54,0 = 15,0.
У який бік зміщено рівновагу реакції? Розглянемо вирази ЗДМ та аналоґічні для концентраційної константи. Чим більшою є константа ЗДМ, тим більші величини для продуктів реакції (з додатними показниками ступеня) і тим менші величини для вихідних реаґентів реакції (з від’ємними показниками). Якщо константа дуже велика, то рівновагу реакції зміщено праворуч, у бік продуктів, а якщо дуже мала, то ліворуч, у бік вихідних речовин.
Наприклад, вирішуючи, у який бік зміщено рівновагу реакції взаємодії оцтової кислоти з аміаком, розглянемо лінійну комбінацію реакцій
| HAc | D | H+ + Ac‑, | lg Ka = ‑4,76, | |
| H+ + NH3 | D | NH4+, | lg KH = 9,24, | |
| HAc + NH3 | D | Ac‑ + NH4+, | ‑4,76 + 9,24 = 5,52, |
із якої вилучено іони Н+. Велика константа лінійної комбінації, К = 105,52, свідчить про зміщення рівноваги праворуч.
Розглянемо, чи може Ag2CrO4(s) помітно розчинятися в водяному NH3. Складімо лінійну комбінацію реакцій, із якою вилучено іон Ag+.
| Ag2CrO4(s) | D | 2 Ag+ + CrO42-, | ‑11,92, | |
| Ag+ + 2 NH3 | D | Ag(NH3)2+, | 7,22, | |
| Ag2CrO4(s) + 4 NH3 | D | 2 Ag(NH3)2+ + CrO42-. | 2,52. |
Константа досить велика, отже можна сподіватись на помітний зсув реакції праворуч і розчинення Ag2CrO4(s).
Складніший приклад – зміщення рівноваги реакцій взаємодії фосфорної кислоти, c(H3PO4) = 0,10 моль/л із аміаком, c(NH3) = 0,50 моль/л. Для 3 ступенів іонізації фосфорної кислоти маємо лінійну комбінацію реакцій,
| H3PO4 | D | H+ + H2PO4‑, | lg Ka1 = ‑2,15, | |
| H2PO4‑ | D | H+ + HPO42‑, | lg Ka2 = ‑7,20, | |
| HPO42‑ | D | H+ + PO43‑, | lg Ka3 = ‑12,35, | |
| H+ + NH3 | D | NH4+, | lg KH = 9,24, | |
| H3PO4 + 3 NH3 | D | PO43‑ + 3 NH4+, | lg K = 6,02. |
Оскільки константа є великою, на перший погляд, можна дією NH3 майже повністю перевести NH3 у іон PO43‑. Проте цей висновок невірний, бо на загальну константу вплинув великий внесок від перших ступенів процесу.
Щоб не помилитися, розглянемо процес крок за кроком. На першому етапі константа лінійної комбінації є досить великою. Перейдемо до граничного складу – наближення, за яким реакція протікає до кінця. Замість «шкільних» пропорцій використаємо іншу форму стехіометричних розрахунків – через число перебігів реакції (змінну де-Донде),
x = Dnj / aj, (23)
постійне для усіх реаґентів відношення зміни кількості речовини у перебігу реакції до стехіометричного коефіцієнта. Із (23) маємо
Dnj = nj* − nj = aj x, (24)
де nj та nj* – кількість речовини Aj відповідно перед і після реакції.
Якщо об’єм розчину є постійним, то у цих співвідношеннях замість кількостей речовини, nj, можна уживати концентрації, сj = nj / V, а замість x – відповідну концентраційну величину, х = x / V. Для співвідношень (15) зручною й наочною є схема, остаточна форма якої походить від М. П. Комаря. Реакцію записуємо як звично, а під формулами реагентів у послідовних рядках подаємо cj, Dcj та cj* – алґебраїчну суму попередніх рядків. Простий рядок Dcj можна й не записувати. Для реакцій, що перебігають праворуч, реагент у недостачі шукаємо серед вихідних речовин, із aj < 0, знаходячи змінну де-Донде, що обертає у 0 концентрацію сj* реагенту Аj. Із цих оцінок для усіх вихідних реагентів виберемо найменшу (інакше з’являться сj* < 0). Формальний математичний запис знайденого граничного числа перебігів, xlim , це
xlim = min {cj / aj | aj < 0}. (16)
Тут min – знак мінімального значення серед множини з елементами (cj / aj).
Для першого ступеня передачі іона Н+ від H3PO4 до NH3 маємо схему граничної зміни концентрацій
| H3PO4 | D | H+ | + H2PO4‑, | ‑2,15, | ||
| H+ | + NH3 | D | NH4+, | 9,24, | ||
| NH3 | + H3PO4 | D | NH4+ | + H2PO4‑, | 7,09, | |
| c | 0,5 | 0,1 | ||||
| Dclim | ‑ 0,1 | ‑ 0,1 | 0,1 | 0,1 | ||
| clim | 0,4 | 0,1 | 0,1 |
Із двох величин, (‑0,5 моль/л) / (‑1) = 0,5 моль/л для H3PO4 та (‑0,1 моль/л) / (‑1) = 0,1 моль/л для NH3, виберемо меншу. Це хlim = 0,1 моль/л. На другому етапі, використовуючи як вихідні граничні концентрації з попереднього етапу, маємо
| H2PO4‑ | D | H+ | + HPO42‑, | ‑7,20, | ||
| H+ | + NH3 | D | NH4+, | 9,24, | ||
| NH3 | + H2PO4‑ | D | NH4+ | + HPO42‑, | 2,04, | |
| c | 0,4 | 0,1 | 0,1 | |||
| Dclim | ‑ 0,1 | ‑ 0,1 | 0,1 | 0,1 | ||
| clim | 0,3 | 0,2 | 0,1 |
На третьому етапі ухиляємось від переходу до граничного складу, бо для лінійної комбінації
| HPO42‑ | D | H+ + PO43‑, | lg Ka3 = ‑12,35, | |
| H+ + NH3 | D | NH4+, | lg KH = 9,24, | |
| HPO42‑ + NH3 | D | PO43‑ + NH4+, | lg K = ‑3,11, |
константа є малою.
Як записувати рівняння реакцій у лабораторних журналах?Виконуючи хімічні реакції з якісного аналізу, трудомісткість яких порівняно невелика, здобуваємо хімічну ерудицію не тільки з якісних реакцій, а й з процесів переводу проби у розчин та відокремлення компонентів. Обґрунтовуючи спостереження, наводимо відповідні хімічні реакції. Повний список реакцій за довідковою літературою занадто великий і, щоб його скласти, потрібні значні витрати часу. Краще розвивати здатність відрізняти головне від другорядного, й реакції з малим виходом взагалі не наводити.
Недоцільно вживати формальні записи реакцій у «іонному» або «молекулярному» вигляді. Намагаємось, щоб у реакціях брали участь реаґенти, що переважають у розгляданій системі. За такими реакціями легше оцінювати рівноважний склад, обґрунтовуючи певну операцію аналізу. Уникаймо записів формул частинок, таких як сильних електролітів HCl або NaCl, що не існують або майже не існують у системі. Як учасників реакції зразу вказуємо відповідний реаґент – іон H+ або Cl‑. Запис
HCl D H+ + Cl‑ вважаємо за неприпустимий,
бо реакція не є оборотною (HCl у розчині не існує), а запис
HCl ® H+ + Cl‑ є припустимим для початківця,
але краще і його уникати, залишаючи в уяві.
Записуємо ті форми (у тому числі слабких електролітів), що, за наближеним розрахунком, переважають у конкретній системі. Це можуть бути як молекули, так і іони. Слідкуйте, щоб у реакціях (крім самого автопротолізу води) не зустрічались одночасно іони Н+ та ОН‑. Який із них слід залишити у реакції, визначаємо логічно – кислу чи лужну реакцію створюють у системі додані реагенти. Вирішити це здебільшого легко, бо для бажаних ефектів у систему часто вводять у надлишку або кислоту або основу. Якщо все ж у реакції маємо Н+ та ОН‑, слід, включивши автопротоліз води у лінійну комбінацію, вилучити з неї небажаний іон.
Як незаряджені частинки, записуємо також формули речовин у твердих та газоподібних фазах, як у розчинах у неіонізуючих розчинниках (із малою діелектричною постійною). Полегшуючи уявлення про ЗДМ для конкретних реакцій, позначимо фазу, в якій міститься реагент. У довідкових таблицях речовину в твердій фазі позначено через (s), а у газоподібній фазі через (g) після відповідної хімічної формули. Замість цього можна вживати стрілки вниз або вгору, тобто ¯ та . Додержуйтесь одного стилю, бо їх змішування не справляє доброго враження.
Не варто прагнути до надмірного лаконізму в записах. Часто краще навести декілька реакцій – спочатку тих, за якими перетворюються вихідні реагенти. У наближених теоретичних обґрунтуваннях для таких реакцій зазвичай переходимо до граничного складу. Уже наприкінці записуємо так звані «аналітичні» реакції за участю переважаючих компонентів, що приводять до появи сиґналу (утворення чи розчинення осаду, забарвлення, тощо), чи до зменшення сиґналу від заважаючи речовин. Так, розчиняючи Ag2S(s) в азотній кислоті, c(HNO3) = 3 моль/л, записуємо лінійну комбінацію реакцій
| Ag2S(s) | D | 2 Ag+ + 2 S2‑, | ‑50,1, | |
| S2‑ ‑ 2 е‑ | D | S(s, ромбічна), | 15,7, | |
| NO3‑ + 4 H+ | D | NO(g) + 2 H2O, | 48,7, | |
| 3 Ag2S(s) + 2 NO3‑ + 8 H+ | D | 6 Ag+ +3 S(s) +2 NO(g) +4 H2O | ‑5,8, |
де про процес дисоціації сильної кислоти НNO3 навіть не згадуємо.
Розглянемо ще приклад – якісну пробу на присутність Mg2+. До 2 крапель досліджуваного розчину додають 2 краплі розчину з с(HCl) = 3 моль/л та 2 краплі насиченого водяного розчину Nа2HPO4. По краплях, перемішуючи, додають розчин із с(NH3) = 3 моль/л. У присутності Mg2+ випадає білий осад MgNH4PO4(s), розчинний у кислотах.
Дисоціацію HCl та Nа2HPO4 (як солі Nа+), сильних електролітів, не записуємо. Зважаючи на послідовність додавання реагентів, довелося б почати з реакцій
2 H+ + HPO42‑ D H3PO4 ,
H3PO4 + 2 NH3 D 2 NH4+ + HPO42‑.
Абстраґуючись від цієї послідовності, можна записати лише нейтралізацію Н+ (від сильної HCl) основою NH3 та лінійну комбінацію, відповідальну за спостережений ефект:
| HPO42- | D H+ + PO43- , | ‑lg KH1 = ‑12,3, | |
| NH3 + H+ | D NH4+ , | lg KH = 9,24, | |
| Mg2+ + NH4+ + PO43- | D MgNH4PO4(s), | ‑lg Ks = 12,6, | |
| Mg2+ + NH3 + HPO42- D MgNH4PO4(s), | lg K = 9,49. |
Такий запис відповідає переважаючим формам, NH3 та HPO42- допоміжних реагентів. Це, як підготовка до подальших теоретичних досліджень, краще, ніж вихідна реакція (з константою Ks).
Обговоримо ще факт, коли осад AgCl(s) розчиняється у концентрованій HCl. Розводячи цей розчин водою, знову одержуємо каламуть.
Розчинення спричиняється утворенням комплексів із надлишком Cl‑. У лабораторному журналі записуємо лінійну комбінацію реакцій,
| AgCl(s) | D Ag+ + Cl‑, | lg Ks = ‑9,75, | |
| Ag+ + 3 Cl‑ | D AgCl32‑, | lg b3 = 6,0 [I = 4], | |
| AgCl(s) + 2 Cl‑ | D AgCl32‑, | lg Ks3 = ‑3,75. |
Із ЗДМ цієї реакції,
[AgCl32‑] / [Cl‑]2 = Ks3,
бачимо, що, розводячи розчин у n разів, зменшуємо чисельник у n разів, а знаменник – у n2 разів. Отже, дріб збільшується у n разів. Щоб виправити цей зріст (дріб – постійна величина, що дорівнює Ks3 !), реакцію зміщуємо ліворуч. Тоді чисельник – концентрація продукту, [AgCl32‑], зменшитися, а знаменник – концентрація вихідної речовини, [Cl‑], зросте. Обидва ці ефекти зменшать дріб, аж поки вона не стане знову рівною константі Ks3. Щоб пояснити ефект, досить наведених якісних доказів: зміщуючи реакцію ліворуч, збільшуємо кількість AgCl(s), твердої фази.
Якби утворювався лише комплекс AgCl2‑, за реакцією
AgCl(s) + Cl‑ D AgCl2‑ ,
то істотних змін від розведення розчину не слід чекати, бо його вплив на чисельник і знаменник був би однаковий.
Такий самий ефект дав би і комплекс AgCl43‑. Проте його константа й сама наявність точно не встановлені, деякі фахівці піддають їх сумніву.
6. КОНЦЕНТРАЦІЙНО-ЛОГАРИФМІЧНІ ДІАГРАМ (КЛД)
КЛД для гетероґенних систем.ЗДМ – одночленний алґебраїчний вираз, із різними показниками ступеня при рівноважних концентраціях. Форма ґрафіків залежності між концентраціями різна, й їх незручно будувати як допоміжний засіб теоретичних досліджень. Але логарифми рівноважних концентрацій залежать один від одного лінійно, й їх графіки легко будувати й сприймати. У логарифмічних координат є ще одна перевага: за ними можна вивчати як великі, так і малі рівноважні концентрації – а рівноважні концентрації продуктів змінюються на багато порядків!
Концентраційно-логарифмічні діаґрами (КЛД) – це сукупність ґрафіків логарифмів рівноважних концентрацій продуктів реакцій як функцій так званої «головної змінної», показника для одного з реаґентів, pX = ‑ lg [X]. Здебільшого, X – або іон водню H+ (тоді pX = pH), або ліґанд L у комплексах, або електрон e- у відновленні,
pe = E / k,
де k – множник Нернста. Часто потрібен лише ескіз КЛД, без деталей, де обмежуються частинами ґрафіків для найбільших концентрацій продуктів реакцій та самої [X]. Їх зручно будувати і сприймати зверху вниз та справа наліво – так, як ми пишемо тексти. Саме таким умовам відповідають згадані координати КЛД, вироблені скандинавською педагоґічною школою.
У рівняннях ЗДМ для гетероґенних систем звичайно 2 змінних – незалежна («головна») і залежна (логарифм концентрації продукту), і ґрафік – пряма лінія.
Розглянемо приклад – КЛД (головна змінна pCl) для комплексів у насиченому розчині AgCl(s). Логарифми констант – для 20 оС та I = 4:
AgCl (s) D Ag+ + Cl‑, lg Ks0 = ‑10,40,
Ag+ + n Cl‑ D AgCln1‑n,
lg bn = 3,45 (n = 1), 5,57 (n = 2), 6,0 (n = 3).
Крок 1. Складімо лінійні комбінації реакцій так, щоб у них із твердої фази, AgCl (s), та пов’язаних із головною змінною іоном Cl‑, утворювався один певний продукт, та розрахуємо
lg Ksn = lg Ks0 + lg bn .
Здобуваємо:
AgCl (s) – Cl- D Ag+, lg Ks0 = -10,40,
AgCl (s) D AgCl, lg Ks1 = -6,95,
AgCl (s) + Cl‑ D AgCl2-, lg Ks2 = -4,73,
AgCl (s) + 2 Cl- D AgCl32-, lg Ks3 = -4,40.
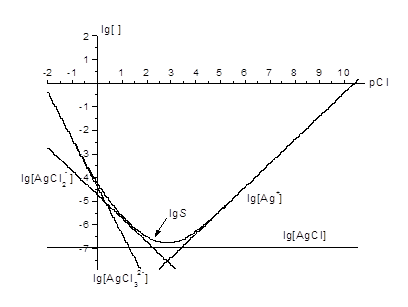
Рис. 1. КЛД для системи AgCl (s) – рCl.
Крок 2. За рівняннями ЗДМ (у лоґарифмічній формі) для цих реакцій,
lg [AgClі1‑і] = lg K sі + (1 – і) pCl,
будуємо прямі (рис. 1). Рівняння для них можна і не записувати. Достатньо уявляти, що прямі перетинають вісь ординат у точках lg K sn та йдуть із танґенсами кутів нахилу, що дорівнюють (із точністю до знака) коефіцієнтові при Cl‑ у наведених вище реакціях. Оскільки AgCl (s) незаряджений, а у Cl‑ заряд дорівнює (‑1), то відповідний танґенс дорівнює зарядові продукту реакції. Напрям нахилу легко збагнути через хімічні уявлення. Так, із зростом рCl зменшується [Cl‑], і, через зсув відповідних рівноваг, зростає [Ag+] та lg [Ag+], не змінюється [AgCl] та зменшуються рівноважні концентрації аніонних комплексів.
Будуючи пряму, обчислімо координати двох її точок. Одну з них, на осі ординат, уже маємо. Другу виберемо далеко від першої, зменшуючи похибки відтворення графіка за лінійкою. Для lg [Ag+] другу точку виберемо на осі абсцис. Танґенс дорівнює 1, й зріст абсциси й ординати однаковий. Отже, ґрафік проводимо через точки (0; ‑ 10,40) та (10,40; 0). Для lg [AgCl32‑] танґенс дорівнює (‑2), і його можна провести через точки (0; ‑ 4,40) та (‑ 4,40 / 2 = ‑ 2,2; 0). Інші ґрафіки будуємо аналоґічно. Абсциси pCl їх точок перетину дорівнюють логарифмам ступінчатих констант стійкості.
Розглянемо ще КЛД (головна змінна pH) для насиченого розчину Al(OH)3(s), де: lg Ks0(Al(OH)3, аморфн.) = -32,34; у комплексів Al3+ із OH-: lg b1 = 9,03, lg b2 = 18,69, lg b3 = 25,99, lg b4 = 32,99, lg b22 = 20,30, lg b43 = 42,05, lg Kw = -14,00.
Крок 1. Складемо лінійні комбінації реакцій:
Al(OH)3 (s) + 3 H+ – 3 H2O D Al3+, lg *Ks0 = 9,66,
Al(OH)3 (s) + 2 H+ – 2 H2O D AlOH2+, lg *Ks1 = 4,69,
Al(OH)3 (s) + H+ – H2O D Al(OH)2+, lg *Ks2 = 0,35,
Al(OH)3 (s) D Al(OH)3, lg *Ks3 = -5,35,
Al(OH)3 (s) – H+ + H2O D Al(OH)4‑, lg *Ks4 = -13,35,
2 Al(OH)3 (s) + 4 H+ – 4 H2O D Al2(OH)24+, lg *Ks22 = 11,64,
3 Al(OH)3 (s) + 5 H+ – 8 H2O D Al3(OH)45+, lg *Ks43 = 15,03.
Лоґарифми констант лінійних комбінацій пов’язані з довідковими даними співвідношенням
lg *Ksji = i lg Ks0 + lg b ji + (j –3 i) lg Kw
(перевірте його!!).
Крок 2. Будуємо прямі (рис. 2)
lg [Ali(OH)j3 i‑j] = lg *Ksji + (j – 3 i) pH.
Як і у попередньому прикладі, рівняння для них майже очевидні: прямі перетинають вісь ординат у точках lg *Ksji та йдуть із танґенсами кутів нахилу, що дорівнюють зарядові продукту реакції. Напрям нахилу легко збагнути через хімічні уявлення. Так, зі зростанням рН зменшується [Н+], і, через зсув відповідних рівноваг, зменшується [Al3+], lg [Al3+] та відповідні величини для катіонних комплексів, не змінюється [Al(ОН)3], зростають рівноважні концентрації аніонних комплексів. Подібні уявлення важливі для самоконтролю при побудові КЛД у вправах.
Не радимо відкладати на осі ординат великі lg *Ksji , бо такі концентрації нездійсненні (хто може зробити розчин із [AlОН2+] = *Ksji = 104,69 моль/л ?!), і КЛД невиправдано витягнеться вгору. Краще вибрати інші точки, наприклад, перетину з віссю абсцис. Оскільки танґенс кута нахилу тут дорівнює (‑2), зарядові іону зі зворотним знаком, то спуск від точки (0; 4,69) до осі абсцис приведе до зміни абсциси на 4,69 / 2 » 2,3 (оцінка наближена, бо точніше на ґрафіку не відкладеш!), і координати точки (2,3; 0). Як другу можна узяти відносно далеку точку, з абсцисою 10. Різниця абсцис двох точок дорівнює 10 – 2,3 = 7,7, а різниця ординат удвічі більша, тобто 2 × 7,7 = 15,4. Координати другої точки (10; ‑15,4). Аналоґічно будуємо інші ґрафіки.
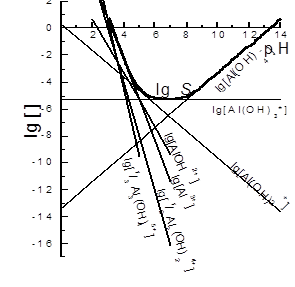
Рис. 2. КЛД для системи Al(OH)3 (s) – рH
Алґоритм побудови КЛД. Узагальнюючи операції, що розглянуті у прикладах, сформулюємо алґоритм:
1. Лінійними комбінаціями привести реакції до
(i / m) MiLj (s або g) + (j - i n / m) L D MiLj, lg Ksji, (17)
й обчислити lg Ksji. У реакції можна включати і розчинник H2O, концентрація якого не входить у ЗДМ.
2. Побудувати прямі
lg [MiLj] = lg Ksji – (j – i n / m) pL, (18a)
або
lg [MiLj] = lg Ksji – (j – i n / m) pL + (i / m) lg p(MiLj (g)), (18b)
де p(MiLj (g)) – заданий парціальний тиск газової фази. Прямі відсікають на осі ординат відрізки lg Ksji, із нахилом до осі абсцис під кутом, тангенс якого дорівнює (j - i n / m).
Радимо не наслідувати алґоритм наосліп, ще й намагаючись знайти відповідність між формулами (17) та (18) із загальними індексами та формулами сполук у Вашій конкретній системі. Краще зрозуміти його операції і будувати відповідні лінійні комбінації реакцій для Вашої системи.
Графіки лоґарифмів розчинності.Розчинність – це концентрація речовини, що перейшла у насичений розчин. Розглянемо реакції у першому прикладі – скільки формульних одиниць AgCl(s) витрачається на одну частинку різних продуктів у розчині. Термін «формульна одиниця» вживають замість «частинка», бо частинки AgCl(s) окремо від твердої фази не існує. Тут по одній формульній одиниці AgCl(s) витрачається у реакціях на одну частинку як Ag+, так і AgCl (у розчині!), AgCl2- та AgCl32-. Розчинність складається із усіх внесків,
S(AgCl) = [Ag+] + [AgCl] + [AgCl2-] + [AgCl32-] = S [AgClj1-j].
Логарифм суми приблизно дорівнює логарифмові найбільшого доданка.
Для прикладу з багатоядерними комплексами розчинність – це
S(Al(OH)3) =[Al3+] + [AlOH2+] + [Al(OH)2+] + [Al(OH)3] + [Al(OH)4-]+ 2 [Al2(OH)24+] + 3 [Al3(OH)45+] = [Al3+] + [AlOH2+] + [Al(OH)2+] +
+ [Al(OH)3] + [Al(OH)4-] + [(1/2) Al2(OH)24+] + [(1/3) Al3(OH)45+].
Логарифм суми приблизно дорівнює логарифмові найбільшого доданка.
На рис. 1 та 2 ґрафіки логарифмів розчинності наведено жирними лініями. З ґрафіків можна оцінити область мінімуму (значення рCl чи рН), де найефективніше компонент відокремлюється з розчину. Ґрафік
lg [(m / i) MiLj] = lg (i / m) + lg [MiLj] (19)
іде паралельно ґрафікові lg [MiLj] на відстані lg (i / m). Тоді, представляючи lg S як верхню обвідну, слід брати ґрафіки логарифмів рівноважних концентрацій еквівалентів. Користуємось нагодою підкреслити гнучкість поняття еквівалентів. Всупереч традиціям, його можна вживати й при (m / i) > 1.
Умови переважання у гомогенних системах.Розглянемо області pH, де переважають продукти кислотно-основних перетворень,
H+ + Ac- D HAc, lg KН = 4,76,
оцтової кислоти. Згідно ЗДМ,
[HAc] / {[H+] [Ac‑]} = KН, [HAc] / [Ac‑] = KН [H+].
Там, де переважає HAc, тобто там, де [HAc] > [Ac‑], маємо
[HAc] / [Ac‑] = KН [H+] > 1, lg {KН [H+]} > 0, lg KН + lg [H+] = lg KН − pH > 0, lg KН > pH.
Там, де переважає Ac‑, тобто там, де [Ac‑] > [НAc], маємо
[HAc] / [Ac‑] = KН [H+] < 1, lg {KН [H+]} < 0, lg KН + lg [H+ ] =
= lg KН – pH < 0,
lg KН < pH.
Можна знайти межі цих областей, де
[HAc] = [Ac‑], [HAc] / [Ac‑] = KН [H+] = 1, lg {KН [H+]} = 0,
lg KН + lg [H+] = lg KН – pH = 0, lg KН = pH.
Неважко визначити, що переважає права сторона й ліва сторона цієї межі. Зі спадом рН (зростанням [H+]) рівновага реакції зміщується праворуч, у бік зв’язування H+. Отже, при рН, менших за значення на межі, переважатиме НАс, а при рН, більших за значення на межі, переважатиме Ас‑.
Зобразимо наочно області переважання на осі рН,
| НАс | Ас‑ 0 | 4,76 | 10 | 14 | pH |
Тепер розглянемо області переважння продуктів кислотно-основних перетворень фосфатної кислоти. Тут
H+ + PO43‑ D HPO42‑, lg KH1 = 12,35,
H+ + HPO42‑ D H2PO4‑, lg KH2 = 7,20,
H+ + H2PO4‑ D H3PO4, lg KH3 = 2,15.
Межею областей для HPO42‑ та PO43‑ є рН = lg KH1 = 12,35, межею областей для H2PO4‑ та HPO42‑ є рН = lg KH2 = 7,20, а межею областей для H3PO4 та H2PO4‑ є рН = lg KH3 = 2,15,
| Н3РО4 | Н2РО4‑ | НРО42‑ | РО43‑ 0 | 2,15 | 7,20 | 12,35 | pH |
Нейтральне середовище відокремлює області переважання H+ та OH‑ – продуктів автопротолізу H2O,
H2O D H+ + OH‑, lg Kw.
Тут немає аналоґу M, бо концентрацію H2O не вводимо до ЗДМ. Залежність [H+] та [OH‑] -
[OH‑] = Kw / [H+], lg [OH‑] = lg Kw + pH.
У кислому розчині переважає H+, [H+] > [OH‑], у лужному – OH‑, [H+] < [OH‑], нейтральний є межею,
[H+] = [OH‑], pH = - (lg Kw) / 2.
Усупереч розповсюдженому твердженню, у нейтральному середовищі не завжди pH = 7, бо на lg Kwс впливають температура, коефіцієнти активності, розчинник.
Колір індикаторів. Перехідному забарвленню приблизно відповідає окіл межі областей переважання
lg KHi − 1 < pH < lg KHi+ 1.
Дата добавления: 2016-08-07; просмотров: 1200;
