НЕЛІНІЙНІ ЕКОНОМЕТРИЧНІ МОДЕЛІ.
У реальних економічних умовах залежність між змінними може адекватно представлятися, як правило, у нелінійній формі. Ця залежність описується формулою
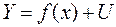 ,
,
де 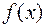 — нелінійна функція аргумента
— нелінійна функція аргумента 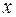 ,
, 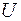 — випадковий чинник.
— випадковий чинник.
Відповідна економетрична модель має вид:
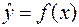 .
.
Вид економетричної моделі вибирається на основі графічного зображення у системі координат ( 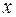 ,
, 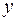 ) статистичної інформації (побудови діаграми розсіювання).
) статистичної інформації (побудови діаграми розсіювання).
Розглянемо найважливіші нелінійні економетричні моделі.
Гіперболічна (зворотна) залежність має вид
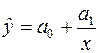 .
.
Вона зводиться до лінійної заміною 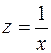 . Одержимо
. Одержимо
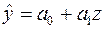 .
.
Перевірка моделі на адекватність та побудова прогнозу здійснюється, як і для лінійної моделі, з урахуванням розглянутої заміни змінної 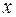 .
.
Задача 5.1. Використати гіперболічну модель для дослідження залежності собівартості 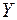 (гр.од./шт.) від кількості виготовленої продукції
(гр.од./шт.) від кількості виготовленої продукції 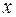 (шт.). Наведена статистична інформація для показників
(шт.). Наведена статистична інформація для показників 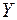 і
і 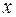 :
:

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
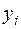
| ||||||||||

|
Потрібно знайти статистичні оцінки параметрів лінійного рівняння регресії.
¡ Статистичні оцінки 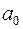 ,
, 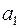 параметрів
параметрів 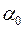 та
та  гіперболічного рівняння регресії, із врахуванням заміни
гіперболічного рівняння регресії, із врахуванням заміни 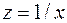 , задовольняють системі нормальних рівнянь (2.12):
, задовольняють системі нормальних рівнянь (2.12):
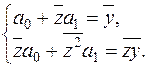
Для знаходження коефіцієнтів цієї системи складемо розрахункову табл. 5.1.
Таблиця 5.1

| 
| 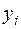
| 
| 
|  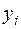
|
| 1 | |||||
| 2 | 0,5 | 0,25 | 18,5 | ||
| 3 | 0,33 | 0,11 | 11,33 | ||
| 4 | 0,25 | 0,06 | 5,25 | ||
| 5 | 0,2 | 0,04 | 5,8 | ||
| 6 | 0,17 | 0,03 | 4,5 | ||
| 7 | 0,14 | 0,02 | 3,57 | ||
| 8 | 0,13 | 0,02 | |||
| 9 | 0,11 | 0,01 | 2,56 | ||
| 10 | 0,1 | 0,01 | 2,2 | ||
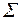
| 2,93 | 1,55 | 96,71 |
Використовуючи нижній рядок табл. 5.1, отримаємо (обсяг вибірки 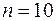 ):
):
 ;
; 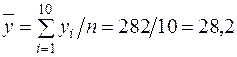 ;
;
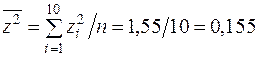 ;
; 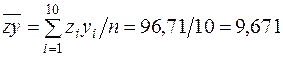 ;
;
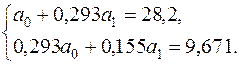
Розв’язок цієї системи рівнянь згідно із формулами (2.13):
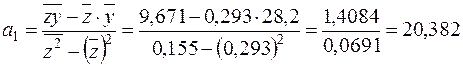 ,
,
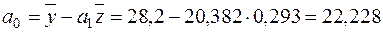 .
.
Отже, емпіричне рівняння регресії має такий вигляд:
 .
.
Для знаходження та оцінки значущості коефіцієнтів регресії 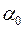 та
та 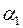 , точкової оцінки дисперсії збурень, вибіркового коефіцієнта детермінації, коефіцієнта кореляції та побудови для них довірчих інтервалів можна використати розглянуті в §2 методи дослідження лінійної моделі парної регресії. При цьому необхідно здійснити потрібну заміну переходу від нелінійної моделі до лінійної. ¥
, точкової оцінки дисперсії збурень, вибіркового коефіцієнта детермінації, коефіцієнта кореляції та побудови для них довірчих інтервалів можна використати розглянуті в §2 методи дослідження лінійної моделі парної регресії. При цьому необхідно здійснити потрібну заміну переходу від нелінійної моделі до лінійної. ¥
Степенева (мультиплікативна) залежність має наступний вид
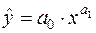 ,
,  ,
,  .
.
Її графік зображено на малюнку 5.1. Степенева залежність використовується для моделювання ситуацій, в яких ріст витрат 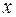 деякого ресурсу обумовлює необмежене збільшення випуску
деякого ресурсу обумовлює необмежене збільшення випуску 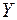 .
.

Малюнок 5.1.
Вона зводиться до лінійної моделі логарифмуванням з довільною основою, наприклад,  . Тоді отримаємо співвідношення
. Тоді отримаємо співвідношення
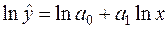 .
.
Застосуємо такі заміни:
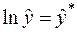 ,
,  ,
,  .
.
Отримаємо рівняння
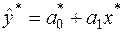 .
.
Експоненціальна (показникова) модель записується так:
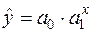 ,
,  ,
, 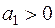 ,
, 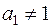 .
.
Для одержання лінійної залежності застосуємо логарифмування. Тоді
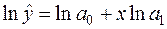 .
.
Здійснивши заміну змінних 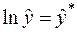 ,
,  ,
, 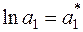 , отримаємо
, отримаємо
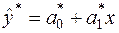 .
.
Криві з границею росту і точкою перегину часто використовуються для статистичного аналізу попиту на деякі нові товари. Такою кривою є, наприклад, крива Джонсона:
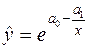 ,
,  ,
, 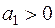 .
.
Її графік зображено на малюнку 5.2.

Малюнок 5.2.
Знайдемо логарифми обох частин кривої Джонсона:
 .
.
Замінивши 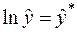 ,
,  , одержимо лінійну залежність
, одержимо лінійну залежність
 .
.
Для моделювання немонотонних (коливних) процесів набули широкого використання многочлени (поліноми)
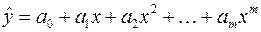 .
.
Якщо всі статистичні значення  (
( 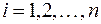 ) різні, то, як відомо з теорії інтерполяції, через
) різні, то, як відомо з теорії інтерполяції, через 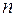 точок можна єдиним способом привести многочлен степені
точок можна єдиним способом привести многочлен степені  .
.
Для одержання лінійної моделі використаємо заміну 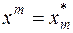 . Одержимо
. Одержимо
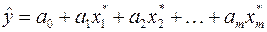 .
.
Ця множинна лінійна залежність з числом змінних 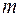 ,
, 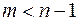 .
.
При дослідженні залежності обсягу податкових надходжень 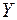 від величини податкової ставки
від величини податкової ставки 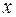 застосовують криву Лаффера
застосовують криву Лаффера
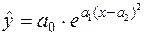 .
.
Тут 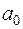 ,
, 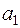 ,
, 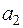 — невідомі коефіцієнти, які визначаються на основі статистичної інформації. Логарифмуємо обидві частини цієї залежності. Маємо
— невідомі коефіцієнти, які визначаються на основі статистичної інформації. Логарифмуємо обидві частини цієї залежності. Маємо
 .
.
Використаємо заміни змінних 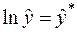 ,
, 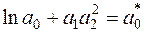 ,
, 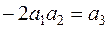 . Матимемо многочлен степені 2
. Матимемо многочлен степені 2
 .
.
Коефіцієнти 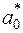 ,
,  ,
, 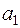 знаходимо як розв’язок такої системи лінійних рівнянь
знаходимо як розв’язок такої системи лінійних рівнянь
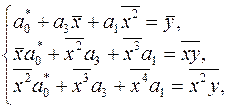
де 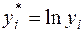 ,
, 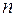 — число статистичних значень кожної із змінних
— число статистичних значень кожної із змінних 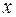 ,
, 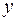 .
.
Графік кривої Лаффера зображено на малюнку 5.3.

Малюнок 5.3.
Для опису процесів в демографії, маркетингу застосовують криву Гомперця
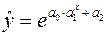 ,
,  .
.
Логарифмуванням ця крива зводиться до модифікованої експоненціальної моделі
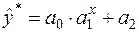 ,
,
де 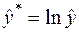 .
.
Графік цієї залежності наведено на малюнку 5.4.


Малюнок 5.4.
Зворотною до модифікованої експоненти є логістична крива
 ,
,  ,
,  ,
, 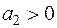 .
.
Її графік зображено на малюнку 5.5.

Малюнок 5.5.
Дата добавления: 2016-06-13; просмотров: 2296;
