Метод матеріального балансу при розрахунках рівноважного складу розчинів
При розчиненні у воді сполук – сильних електролітів (які повністю розпадаються на іони) – за умови іони, що утворюються у розчині не вступають в інші реакції, рівноважний склад частково можна описати на основі рівнянь матеріального балансу.
приклад 1. Розчиненням у воді солі MgCl2 приготували розчин із концентрацією 0,25 моль/л. Який рівноважний склад розчину?
Розв’язання: При розчиненні у воді MgCl2 кожна умовна молекула породжує 1 іон Mg2+ та два іони Cl-. Значить [Mg2+] = 0,25 моль/л, a [Cl-] = 0,50 моль/л. Оскільки за участю води в такому розчині проходить тільки реакція дисоціації
H2O D H++OH- KW = [H+]·[OH] = 10-14, (a)
то матеріальний баланс по протонам (або по гідросид-іонам) має вид:
t(H+) = [H+] – [OH] = 0 (b)
з рівняння (а) виразимо рівноважну концентрацію іона гідроксиду [OH] = kw/[H+] і підставимо в рівняння (b):
[H+] – kw / [H+] = 0
[H+]2 = kw =10-14 [H+] =10-7 моль/л,
І в результаті [OH] = 10-14/10-7=10-7
Відповідь: [Mg2+] = 0,25; [Cl-] = 0,50 моль/л; [H+] =
= [OH-] =10-7 моль/л.
Якщо іони, що утворились при розчиненні солі беруть участь в інших реакціях із утворенням нової частинки, кожна така реакція характеризується окремою константою рівноваги, а значить формується незалежне рівняння константи рівноваги закону діючих мас. У результаті число рівнянь дорівнює числу нових невідомих рівноважних концентрацій іонів і молекул. Із указаного в цьому абзаці випливає висновок про те, що об’єднання рівнянь матеріального балансу та рівнянь констант ЗДМ для рівноважної системи розчину з відомими загальними концентраціями класів компонентів забезпечує розрахунки рівноважного складу.
Приклад 2. Розчиненням у воді солі HCOOAg приготували розчин з концентрацією 0,1 моль/л. Який рівноважний склад розчину? (HCOO- – аніон мурашиної кислоти, форміат-іон).
Розв’язання: У розчині присутні такі частинки: Ag+, HCOO-, H+, OH-, AgOH, Ag(OH)2-, HCOOH.
Коментарі: Перші дві частинки утворились при розчиненні у воді мурашинокислого срібла. Наступні дві – при дисоціації води. гідроксокомплекси срібла утворились при взаємодії з водою іонів Ag+.
1) Ag+ + H2O D AgOH + H+ βОH1KW =102·10-14 = 10-12
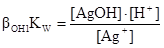 . (a)
. (a)
Константа ЗДМ для реакції (1) складається з констант двох реакцій (b), (c):
 H2O D H+ + OH- KW = 10-14 =
H2O D H+ + OH- KW = 10-14 = 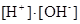 (b)
(b)
Ag+ + OH- D AgOH βОH1 = 102 =  (c)
(c)
----------------------------------------------------------------------
Ag+ + H2O D AgOH + H+ βОH1KW = 102·10-14.
Аналогічно константа ЗДМ (d) для реакції (2) складається з констант двох реакцій (e),(g):
2) Аg+ + 2H2OD Ag(OH)2- +2H+ βОH2KW2 = 104·(10-14)2 =10-24 βОH2KW2 = 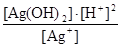 . (d)
. (d)

 2 H2O D H+ + OH- KW2 = 10-14 (e)
2 H2O D H+ + OH- KW2 = 10-14 (e)
 Ag+ + 2OH- D Ag(OH)2- βОH2 = 104 (g)
Ag+ + 2OH- D Ag(OH)2- βОH2 = 104 (g)
--------------------------------------------------
2H2O + Аg+DAg(OH)2- +2H+ βОH2KW2 = 10-24.
Остання частинка – недисоційована форма мурашиної кислоти, утворюється в результаті взаємодії з протонами води форміат-іону:
HCOO- + Н+ D HCOOН βH1 = 103,745 = 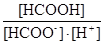 . (h)
. (h)
Звертаємо увагу!Щоб назвати всі частинки, що утворюються у розчині, необхідно проконтролювати наявність констант ЗДМ (див. довідкові таблиці констант рівноваг) між іонами, що утворились при розчиненні сполуки у воді, катіонів з іонами ОН- аніонів з іонами Н+.
Іони і молекули, що присутні в розчині утворюють класи частинок – групи іонів та молекул, до складу яких входить один і той же атом, або одна і таж група атомів. У нашій задачі утворилось три класи частинок:
1) клас іонів срібла: Ag+, AgOH, Ag(OH)2-;
2) клас форміат іонів: HCOO-, HCOOH;
3) клас іонів водню: H+, OH-, AgOH, Ag(OH)2-, HCOOH.
Для кожного з трьох класів записують рівняння матеріального балансу:
t(Ag+) = [Ag+]+[AgOH]+[Ag(OH)2-] = c(HCOOAg) = 0,1 (k)
t(HCOO -) = [HCOO-]+[ HCOOH] = c(HCOOAg) = 0,1 (l)
t(H+) = [H+]+[ HCOOH] – [OH] – [AgOH] –2[Ag(OH)2-] = 0 (m)
З рівнянь (a), (d), (h) виражають відповідно [AgOH], [Ag(OH)2-], [HCOOH] підставляють їх у рівняння (k) та (l) і отримують відповідно вирази для [Ag+] та [HCOO-]
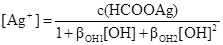 , (n)
, (n)
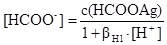 . (o)
. (o)
Після підстановки рівнянь (n) і (o) в рівняння ЗДМ (a), (d). (h) виражають [HCOOH], [AgOH], [Ag(OH)2-] і підставляють у рівняння матеріального балансу по водню (m), додатково замінюють [OH] на KW/[H+]. У результаті отримують рівняння, в якому лише одна невідома. Це – [H+]·[H+]+ 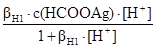 –
– 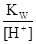 –
– 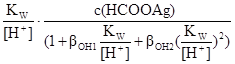 –2
–2 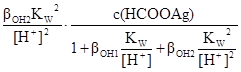 = 0. (p)
= 0. (p)
Для формування системи рівнянь для розрахунку рівноважного складу розчину методом матеріального балансу зручно скористатися матрицею стехіометричних коефіцієнтів:
1) Виділяють незалежні компоненти багатокомпонентної системи – компоненти, які присутні в розчині і не утворюються при взаємодії з іншими іонами (молекулами). При взаємодії з іншими частинками в розчині кожний із незалежних компонентів утворює окремий клас. Для прикладу 2 – це Ag+, HCOO- і H+.
2) Будують матрицю стехіометричних коефіцієнтів.
У 2-4 стовпчиках матриці вказують стехіометричні коефіцієнти в реакціях утворення продуктів за участю незалежних компонентів. 5 стовпчик – це продукти реакції, серед яких у верхній частині вказують і незалежні компоненти. Це значить, що серед продуктів будуть усі іони і молекули, що присутні в розчині. У 6 стовпчику вказують логарифми констант рівноваги утворення кожного з продуктів. Для незалежних компонентів константа рівноваги тотожна одиниці. Рівноважна концентрація кожного з продуктів дорівнює добутку константи рівноваги і рівноважних концентрацій незалежних компонентів у степенях відповідних стехіометричних коефіцієнтів. Наприклад, (див. 7 строчку):
[Ag(OH)2-] = 10-24[Ag+][H+]-2.
Матриця стехіометричних коефіцієнтів
| стехіометричні коефіцієнти при взаємодії незалежних компонентів | |||||
| № п\п | Ag+ | HCOO- | H+ | Продукт реакції | lgK |
| Ag+ | |||||
| HCOO- | |||||
| H+ | |||||
| HCOOH | lgβH1 =3,745 | ||||
| -1 | OH- | lgKw = -14 | |||
| -1 | AgOH | lgβOH1+lgKw= -12 | |||
| -2 | Ag(OH)2- | lgβOH2+2lgKw= -24 |
Рівняння матеріального балансу для кожного класу (див. рівняння (k, l, m)) дорівнюють сумі добутків рівноважних концентрацій продуктів (стовпчик 5) та стехіометричних коефіцієнтів відповідного незалежного компонента.
підстановка в рівняння матервльного балансу по водню (m) дає рівняння (p).
Після зведення у рівнянні (p) до спільного знаменника чисельник утворює рівняння з невідомим у 5 степені.
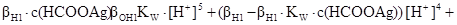
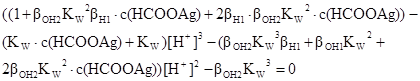
Звертаємо увагу!
Після підстановки значень отримуємо:
103,745·10-1·10210-14·[H+]5 + (103,745–103,745·10-14·0,1) [H+]4 +
+(1+104·10-28·103,745+2·103,745·104·10-28·0,1) – (10-14·0,1+10-14)) · ·[H+]3 – (104·10-42·103,745 +102 10-28+2·104·10-280,1· [H+]2–104·10-28 = 0.
10-9.45 [H+]5 +103,745 [H+]4+[H+]3+10 -25,824· [H+]2 – 10-24 = 0.
Після зведення подібних:
[H+]5 + 1013,195[H+]4 +109,45 [H+]3 +10 -16,374·[H+]2 – 10-14,55 = 0.
Після розвязання рівняння значення рівноважної концентрації [H+] підставляють у рівняння (b), (n), (o) – знаходять [OH], [Ag+], [HCOO-]. Виходячи з останніх за рівняннями (a), (c) знаходять концентрації [Ag(OH)], [Ag(OH)2- ].
Зрозуміло, що розв’язання такого рівняння високої степені досить громіздке, воно незручне для створення комп’ютерних програм розв’язання, потребує алгебраїчних спрощень. Щоб не мати справу з громіздкими рівняннями, треба виділити серед хімічних рівноваг у розчині таку рівновагу (таку хімічну реакцію), для якої значення константи рівноваги з участю переважаючих компонентів (часто вони є незалежними) найбільша. Якщо таку рівновагу вдалося знайти, то використовують рівняння закону діючих мас для цієї рівноваги і розраховують рівноважні концентрації учасників реакції за схемою М. П. Комаря.
Стехіометрія реакції та рівень концентрацій реагентів. Якщо константа ЗДМ досить близька до 1, а її логарифм до 0, висновок, у який бік зміщено рівновагу, не такий тривіальний. Для реакції (1) розмірність концентраційної константи ЗДМ – це (моль/л)a, де a = S aj – сума стехіометричних коефіцієнтів при усіх реагентах, крім розчинника, Н2О та реагентів у твердих фазах. Тривіальна оцінка є справедливою, якщо a = 0, або якщо концентрації за порядком величини близькі до 1 моль/л (тоді розмірність Кс істотно не впливає на висновок про напрям реакції). Вплив стехіометричних коефіцієнтів тим більший, чим більше концентрації за порядком величини відрізняються від 1 моль/л. У сумнівних випадках оцінюємо величину зсуву реакції, підставляючи до ЗДМ оцінки концентрацій с*j. Розглянемо дисоціацію іона Cr2O72‑,
Cr2O72‑ + H2O D 2 HCrO4‑, lg K = ‑1,97 [I = 1],
якщо (а) с(Cr2O72‑) = 0,005 моль/л; (b) с(Cr2O72‑) = 5×10‑5 моль/л. Хоч константа досить мала (К » 0,01), а позитивна сума усіх стехіометричних коефіцієнтів, (‑1) + 2 = 1, та мала вихідна концентрація сприяють зсуву рівноваги реакції праворуч. Оцінюючи цей ефект, розрахуємо рівноважний склад, підставляючи до ЗДМ вирази
[Аj] » с*j = сj + х × aj.
Для варіанта (а)
| Cr2O72‑ | + H2O | D | 2 HCrO4‑, | lg K = ‑1,97 | |
| c | 0,005 | - | |||
| Dc | ‑ x | - | 2 x | ||
| [ ] | 0,005 ‑ x | - | 2 x, |
Підставляючи формули з рядка [ ] у ЗДМ, маємо рівняння
(2 x)2 / (0,005 – x) = 10‑1,97, 4 x2 + 10‑1,97x – 0,005×10‑1,97 = 0,
із позитивним коренем x = 2,56×10‑3 моль/л,
[Cr2O72‑] = 0,005 – x = 2,44×10‑3 моль/л,
[HCrO4‑] = 2 x = 5,12×10‑3 моль/л.
Частка вихідного Cr2O72‑, що залишилася при переході до рівноваги, це
x / 0,005 = 0,512, або 51,2 %.
Аналоґічні розрахунки для варіанта (b) дають
x = 4,91×10‑5 моль/л, [Cr2O72‑] = 5×10‑5 – x = 9×10‑7 моль/л,
[HCrO4‑] = 2 x = 9,82×10‑5 моль/л, x / 5×10‑5 = 0,982, або 98,2 %.
Розглянемо ще, яка реакція є відповідальною за розчинення Ag2S(s) у азотній кислоті, c(HNO3) = 3 моль/л. Кислота HNO3 практично є сильною – повністю іонізованою. Отже c(HNO3) = 3 моль/л фактично означає c(H+) = c(NO3‑) = 3 моль/л. Сульфід розчиняється або через кислотно-основні властивості аніону S2‑, що зв’язується з Н+, або через окиснення сульфідної сірки до елементної дії окисника, іона NO3‑. Розглянемо ці можливості. Першій відповідає лінійна комбінація реакцій
| Ag2S(s) | D | 2 Ag+ + 2 S2‑ | lg Ks = ‑50,1 | |
| H+ + S2‑ | D | HS‑, | lg KH1 = 13,9 | |
| H+ + HS‑ | D | H2S, | lg KH2 = 7,02 | |
| Ag2S(s) + 2 H+ | D | 2 Ag+ + H2S, | ‑29,2. |
Для дуже малої К годі сподіватись на помітний зсув рівноваги праворуч.
Другій можливості відповідає лінійна комбінація
| Ag2S(s) | D | 2 Ag+ + 2 S2‑, | ‑50,1, | |
| S2‑ ‑ 2 е‑ | D | S(s, ромбічна), | 15,7, | |
| NO3‑ + 4 H+ | D | NO(g) + 2 H2O, | 48,7, | |
| 3 Ag2S(s) + 2 NO3‑ + 8 H+ D 6 Ag+ + 3 S(s) + 2 NO(g) + 4 H2O. | ‑5,8. |
Ця константа значно більша, ніж попередня, і різні стехіометричні коефіцієнти закликають до докладнішого дослідження. Складімо схему Комаря,
| 3 Ag2S(s) + | 2 NO3‑ + | 8 H+ | D | 3 S(s) + 2 NO(g) + + 4 H2O + 6 Ag+ | ‑5,8 | ||
| c | - | - | |||||
| Dc | - 3 x | ‑ 2 x | ‑ 8 x | - | 6 x | ||
| [ ] | - | 3 ‑ 2 x | 3 – 8 x | - | 6 x |
Розв’язуючи відповідне рівняння ЗДМ,
(6 x)6 / {(3 – 2 x)2 (3 – 8 x)8} = 10‑5,8,
маємо x = 0,080 моль/л, [NO3‑] = 3 – 2 x = 2,840 моль/л, [H+] =
= 3 – 8 x = 2,360 моль/л, [Ag+] = 6 x = 0,480 моль/л, S(Ag2S(s)) = 3 x = 0,24 моль/л, а це не така вже маленька величина!
У рівняння ЗДМ не входив р(NO(g)), парціальний тиск газу, бо у дослідженій моделі процесу ми припускали, що р(NO(g)) = 1 атм, а надлишок газоподібного продукту над цією величиною виходить із розчину – розчин є насиченим відносно продукту NO(g). За довідковими даними, розчинність NO(g) у воді дорівнює 3,3×10‑3 моль/л при 0 оС та 1,05×10‑3 моль/л при 60 оС. За рівнянням реакції, концентрація продукту NO дорівнює 2 x = = 0,160 моль/л, а це істотно перевищує розчинність, і модель підтверджено. У практичній роботі систему підігрівають. Це змінює константи рівноваги (напрям визначається знаком DH реакцій), пришвидшує перетворення, зменшує розчинність NO(g) та сприяє вилученню його з системи. З нашої оцінки випливає можливість процесу й у звичайних умовах.
Нижче наведено кілька прикладів розв’язання задач на розрахунки рівноважного складу розчинів.
Дата добавления: 2016-08-07; просмотров: 1052;
