Уравнения динамики и статики
При проектировании и исследовании САУ необходимо знать уравнения, описывающие их движения. Процессы в САУ описываются дифференциальными, разностными, интегральными и интегро-дифференциальными уравнениями, которые называют ее математической моделью. При исследовании САУ на различных этапах математическая модель может быть различной. Начинают исследования САУ с простейшей математической моделью, а затем ее усложняют, учитывая дополнительные связи и влияния. Такой подход объясняется тем, что к математической модели предъявляются противоречивые требования. Математическая модель должна достаточно полно описывать динамику САУ и при этом быть по возможности простой.
В дальнейшем будут рассматриваться только обыкновенные дифференциальные уравнения, в неявной форме которые могут быть записаны
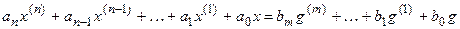 , (3.1)
, (3.1)
или
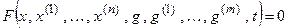 , где (3.2)
, где (3.2)
| x, x(i) | - управляемая (выходная) величина и ее производные 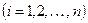 ; ;
| |
| g, g(j) | - задающая (входная) величина и ее производные 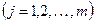 ; ;
| |
| ai и bj | - постоянные коэффициенты, зависящие от параметров системы; | |
| с и m | - числа, определяющие порядок производных 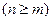 , причем n определяет порядок дифференциального уравнения; , причем n определяет порядок дифференциального уравнения;
| |
| t | - независимая переменная (время). |
Уравнения (3.1) и (3.2) могут быть записаны в явной форме, разрешенные относительно старшей производной (например, (3.2))
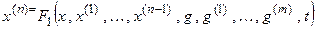 .
.
Данное дифференциальное уравнение в явной форме n-го порядка можно преобразовать в систему n дифференциальных уравнений первого порядка:
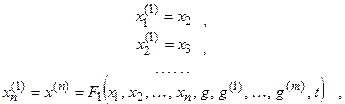
путем введения новых неизвестных
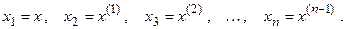
Если в дифференциальное уравнение (3.2) входит n неизвестных функций 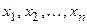 , тогда можно записать систему из n уравнений первого порядка в виде
, тогда можно записать систему из n уравнений первого порядка в виде
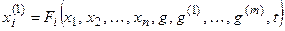 ,
,
где 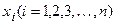 – переменные, характеризующие состояние системы.
– переменные, характеризующие состояние системы.
В векторной форме дифференциальное уравнение будет иметь вид



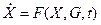
или
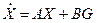 ,
,
| где | X – вектор выходных величин (параметров состояний); |
| G – вектор задающих (входных) величин; | |
| A – матрица объекта управления с элементами aij; | |
| B – матрица задающих величин с элементами bij . |
Широкое применение в ТАУ получила операторная форма записи дифференциального уравнения. Это объясняется тем, что от дифференциального уравнения посредством интегрального преобразования (например, преобразования Лапласа) переходят к операторной форме. Операторное уравнение является алгебраическим и его решение проще, чем дифференциальное. Затем из полученного решения операторного уравнения с помощью обратного преобразования получают решение дифференциального уравнения.
Дифференциальное уравнение (3.1) при нулевых начальных условиях
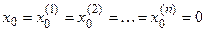
в операторной форме можно записать
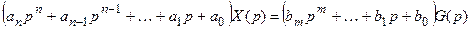
или
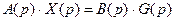 ,
,
где 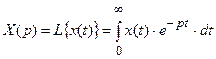 - преобразование Лапласа от
- преобразование Лапласа от 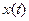 ;
;
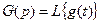 - преобразование Лапласа от
- преобразование Лапласа от  ;
;
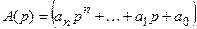 - характеристический многочлен (3.1);
- характеристический многочлен (3.1);
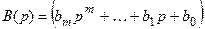 - изображение правой части (3.1);
- изображение правой части (3.1);
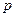 - параметр преобразования Лапласа.
- параметр преобразования Лапласа.
Операторная форма записи дифференциального уравнения, когда начальные условия по всем переменным равны нулю, совпадает с символической формой, когда 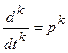 , а p – символ дифференцирования. Поэтому для получения операторной формы записи дифференциального уравнения, когда начальные условия нулевые, применяют приемы символической формы.
, а p – символ дифференцирования. Поэтому для получения операторной формы записи дифференциального уравнения, когда начальные условия нулевые, применяют приемы символической формы.
Уравнение движения САУ в любой форме полностью описывает весь процесс управления, т.е. процесс изменения управляемых величин как в переходном, так и в установившемся режимах.
Под установившимся режимом понимают процесс, при котором регулируемая (управляемая) величина изменяется по закону, определяемому лишь законом изменения задающего воздействия. Установившейся режим САУ, относительно которого рассматривается движение системы в процессе управления, называется исходным.
Переходным режимом называется изменение управляемой величины при переходе САУ из одного в другое установившееся состояние.
Если в установившемся режиме воздействия после их приложения больше не изменяют своих величин во времени, то в САУ устанавливается так называемый статический режим.
Уравнение статики может быть получено из уравнения движения САУ (3.1), если все члены, содержащие производные, приравнять нулю, то есть
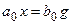 или
или 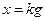 ,
,
где 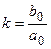 - коэффициент передачи САУ.
- коэффициент передачи САУ.
Графическое отображение данной зависимости, т.е. зависимости между выходной x и входной g величинами САУ в статическом режиме, называется статической характеристикой (рис. 3.1).
 |
Рис.3.1. Статические характеристики элементов САУ
Статические характеристики элементов САУ и систем в целом могут быть как линейными (кривая 1, рис. 3.1), так и нелинейными (кривая 2, рис. 3.1). Если характеристика нелинейная, то необходимо учитывать влияние данной нелинейности на динамику САУ.
Дата добавления: 2016-06-24; просмотров: 2125;
