Классификация систем управления. Как было отмечено ранее существует два взаимосвязанных класса систем управления:

Как было отмечено ранее существует два взаимосвязанных класса систем управления:

- системы автоматического управления (САУ);

- автоматизированные системы управления (АСУ).

А. Классификация САУ

В зависимости от того, какими классами дифференциальных уравнений описываются САУ, их можно укрупненно классифицировать так, как показано на рис. 2.2.

Линейными называют класс систем, описываемый линейными операторными уравнениями (например, линейными дифференциальными уравнениями или их системами), в противном случае система входит в класс нелинейных систем.

Линейными или нелинейными дискретными системами называются такие системы, которые описываются соответственно линейными или нелинейными разностными уравнениями или системами разностных уравнений.

Линейными или нелинейными стационарными системами называются системы, которые описываются дифференциальными уравнениями или системами уравнений с постоянными коэффициентами.

Нестационарными системами (линейными или нелинейными) называют системы автоматического управления, поведение которых описывается дифференциальными уравнениями или системами уравнений с переменными коэффициентами.

Сосредоточенными, или системами с сосредоточенными параметрами называются системы, поведение которых описывается обыкновенными дифференциальными уравнениями.

Распределительные системы – это системы, которые описываются дифференциальными уравнениями в частных производных.

Б. Классификация АСУ

При классификации АСУ целесообразно использовать следующие классификационные признаки:

- степень автоматизации;

- уровень управления;

- интервал управления;

- тип объекта управления и т.д.

По степени автоматизации АСУ могут быть:

- информационными СУ;

- информационн0-советующими СУ;

- управляющими.

1 Математические модели “вход-выход”, “вход-состояние-выход”

На первом этапе расчета и проектирования систем автоматического управления (САУ) ограничиваются качественным описанием систем и в связи с этим рассматривают их функциональные схемы. Такое описание называют содержательным или неформальным. Неформальным описанием САУ называется вся имеющаяся совокупность сведений о ней, достаточная для построения фактического алгоритма ее работы. Неформальное описание системы содержит информацию, достаточную для построения ее функциональной схемы. Последняя же служит основой для разработки формального (математического) описания системы.

Недостаток содержательного или неформального описания систем в том, что такой подход не оперирует количественными характеристиками и, таким образом, наука, в основе которой лежит неформальное описание, не является точной наукой. Для решения же задач исследования и проектирования систем необходимо оперировать количественными характеристиками, определяющими качество ее работы. В связи с этим центральным понятием теории систем является математическая модель или оператор системы.

Под математической моделью САУ понимают количественную формализацию абстрактных представлений об изучаемой системе. Математическая модель – это формальное описание системы с помощью математических средств: дифференциальных, интегральных, разностных, алгебраических уравнений, а также неравенств, множеств и т.д.

Пользуясь понятием системного оператора, можно на единой основе рассмотреть понятие математической модели САУ.

Пусть G и X – множества входных и выходных сигналов САУ. Если каждому элементу gÎG составится в соответствие определенный элемент xÎX, то говорят, что задан системный оператор А.

Связь между входом и выходом системы задается посредством системного оператора A:

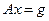и .

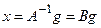Операторное уравнение (или уравнение с оператором A) 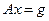следует считать математической моделью САУ, поскольку оно устанавливает количественную связь между входом и выходом 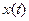системы.

Принципиально важным является ответ на вопрос: как построить оператор системы A?

Важным положением ответа на поставленный вопрос является следующее: в подавляющем большинстве случаев операторное уравнение системы принадлежит к классу дифференциальных уравнений или эквивалентных им интегральных уравнений. Для получения дифференциального уравнения системы в целом обычно составляют описание ее отдельных элементов, т.е. составляют дифференциальное уравнения для каждого входящего в систему элемента.

Совокупность всех уравнений элементов и дает уравнение системы в целом.

Уравнения системы определяют ее математическую модель, которая для одной и той же системы в зависимости от цели исследования может быть разной.

Полезно при решении одной и той же задачи на разных этапах строить разные математические модели: начинать исследование можно с простой модели, а затем ее постепенно усложнять, с тем, чтобы учесть дополнительные физические явления и связи, которые на начальном этапе не были учтены как несуществующие.

Задать оператор системы – это значит задать правило определения выходного сигнала этой системы по ее входному сигналу.