Частотно временной анализ.
Класс Коэна: можно получить бесконечное число частотных распределений. Всё зависит от параметра ядра.
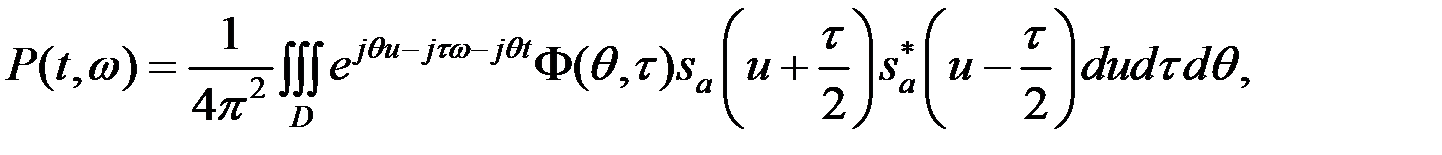(11.4)
где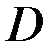 
– область определения сигнала 
; 
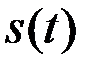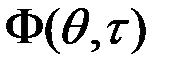– ядро преобразования, определяющее вид и свойства получаемого ЧВР; 
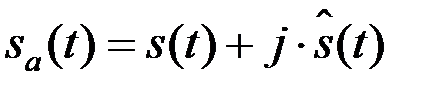– аналитический сигнал анализируемого действительного сигнала 
, 
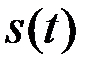– знак комплексного сопряжения.
Преимуществами универсальной формулировки класса Коэна также является то, что:
- путём выбора ядра параметризации 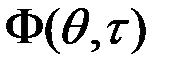возможно получить большинство известных распределений энергии;
- желаемые свойства ЧВР можно эквивалентным образом переформулировать в терминах ограничений на ядро .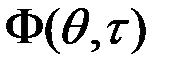
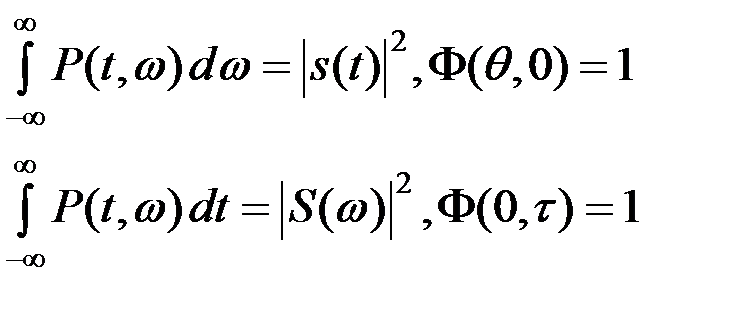(11.5)
Таблица 11.1 – Свойства распределений
| Преобразование сигнала | Сигнал s(t) | Распределение P(t,w) | Требования к ядру F(q,t) |
| Сдвиг по времени | s(t+t0) | P(t+t0,w) | Любое |
| Сдвиг по частоте | S(w+w0) | P(t,w+ w0) | Любое |
| Масштабирование по времени | P(at,w/a) | F(q/a,at)=F(q,t) | |
| Масштабирование по частоте | P(t/b,bw) | F(bq,t/b)=F(q,t) | |
| Обращение по времени | s(-t) | P(-t,-w) | F(-q,-t)=F(q,t) |
Распределение Вигнера-Вилла. Вычисление:
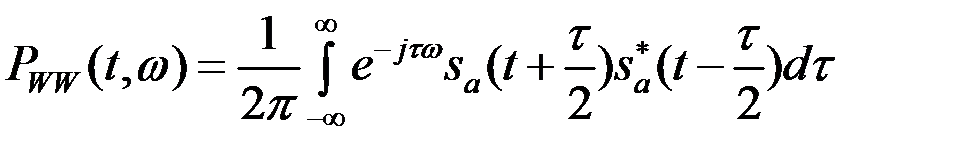(11.6)
Распределение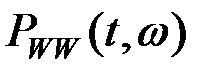 
может принимать только действительные значения (включая отрицательные). Несмотря на высокое разрешение, как по частоте, так и по времени, в распределении может порождать побочные частотные компоненты, затрудняющие анализ сигнала. Это связано с нелинейностью преобразования. Пример частотно-временного распределения Вигнера-Вилла приведен на рис.11.3.
Рисунок 11.3 – ЧВР Вигнера-Вилла
Распределение Цзуя –Уильямса. Вычисляется по (11.7):
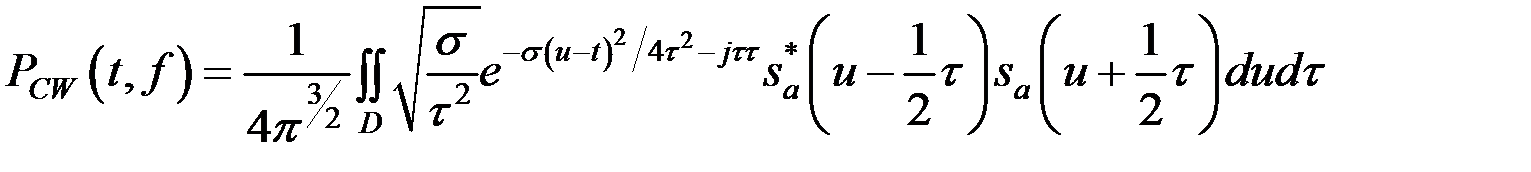(11.7)
Рисунок 11.4 – ЧВР Цзуя-Уильямса
Дата добавления: 2016-06-24; просмотров: 852;