Корреляционный и регрессионный анализ.

Корреляционный анализ позволяет делать статистические выводы о степени зависимости между переменными.

Регрессионный анализ позволяет решать две задачи:

1) устанавливать наличие возможной причинной связи между переменными;

2) предсказывать значения переменной по значениям независимых переменных.

Примеры данных для корреляционного и регрессионного анализа (рис. 6.2-6.3).

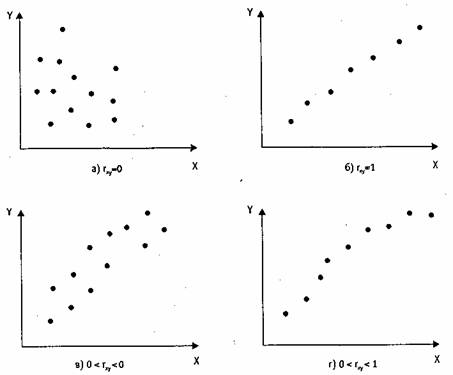Рисунок 6.2 – Исходные данные для анализа

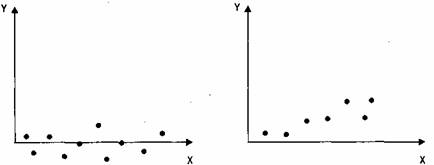
Рисунок 6.3 – Ошибка работы регрессионной модели

Статистическая оценка устойчивости. При статистической оценке устойчивости модели соответствующая гипотеза может быть сформулирована следующим образом: при изменении входной (рабочей) нагрузки или структуры модели закон распределения результатов моделирования остается неизменным.

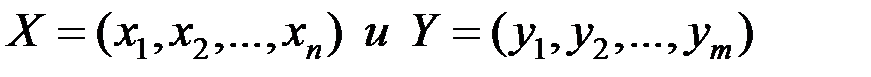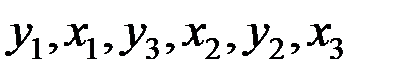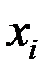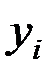Проверку указанной гипотезы Н проводят при следующих исходных данных: есть две выборки , полученные для различных значений рабочей нагрузки; относительно законов распределения X и У никаких предположений не делается. Значения обеих выборок упорядочиваются вместе по возрастанию . Затем анализируется взаимное расположение и . В случае 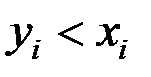говорят, что пара значений 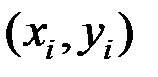образует инверсию .

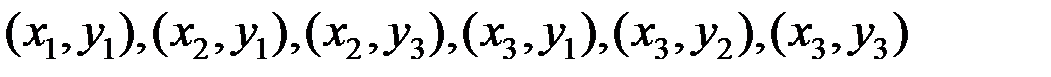Подсчитывают полное число инверсий U. Если гипотеза верна, то U не должно сильно отклоняться от своего математического ожидания : .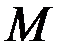

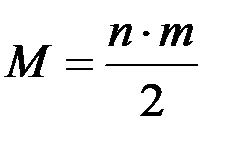Гипотеза не подтверждается если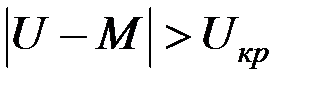
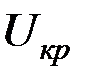( определяют по таблице для заданного уровня значимости)