Лекция 8.Фрактальные модели трафика ТКС
«Модель Клейнрока-Джексона» представляет сеть как множество независимых КС, каждый из которых представляет собой одноканальную СМО с бесконечными очередью и потоком требований. «Аппроксимация независимостью Клейнрока» – допущение о независимости потока в каждом узле, независимости времени поступления заявки и ее длинны от предыдущих заявок, при этом считается, что поток заявок стационарен и время поступления и обслуживания заявок распределены по экспоненциальному закону.
Введение во фракталы. Понятие фрактал введено Б. Мандельбротом в 1975 году. Фрактал – математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения (любая часть фрактала подобна всему множеству целиком). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную размерность. Классификация фракталов приведена на рис. 8.1, примеры – на рис. 8.2-8.4.
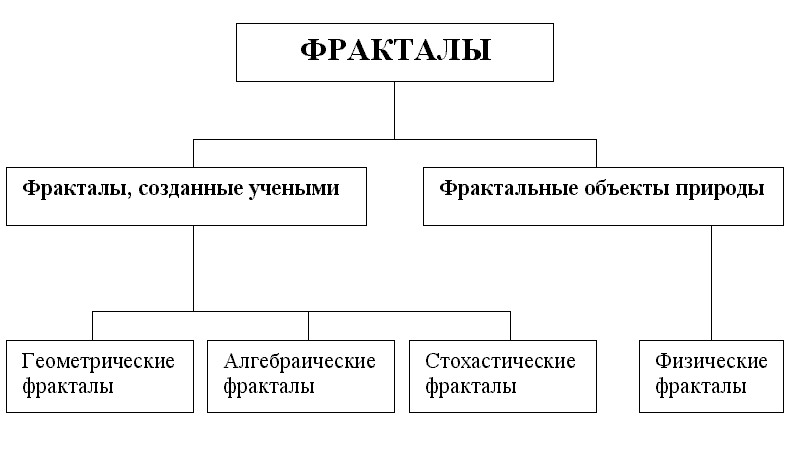
Рисунок 8.1 – Классификация фракталов

Рисунок 8.2 – Треугольник Серпинского

Рисунок 8.3 – Множество Кантора

Рисунок 8.4 – Кривая Коха
Определение самоподобного процесса. Случайный процесс 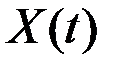 считается самоподобным с параметром Хэрста
считается самоподобным с параметром Хэрста 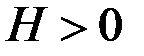 , статистическая характеристика процесса
, статистическая характеристика процесса 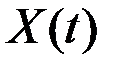 не меняется при масштабировании по амплитуде на
не меняется при масштабировании по амплитуде на 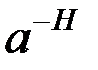 и по времени на
и по времени на 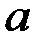 для всех
для всех 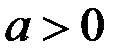 :
:
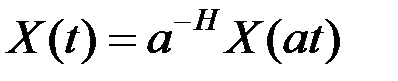 (8.1)
(8.1)
где 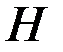 – коэффициент или параметр Хэрста, является мерой самоподобия.
– коэффициент или параметр Хэрста, является мерой самоподобия.
Под самоподобием трафика подразумевается повторяемость распределения нагрузки во времени при различных масштабах времени.
Свойства самоподобных процессов:
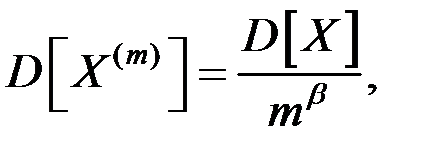 (8.1)
(8.1)
где 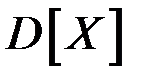 – дисперсия процесса
– дисперсия процесса 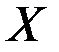 ,
, 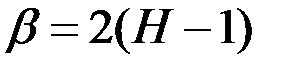 ,
,  – агрегированный процесс с масштабом
– агрегированный процесс с масштабом 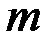 .
.
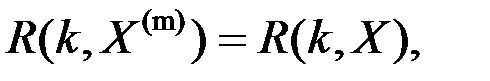 (8.2)
(8.2)
где 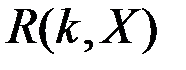 – кореляционная функция,
– кореляционная функция, 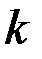 – номер блока,
– номер блока,  – масштаб агрегации.
– масштаб агрегации.
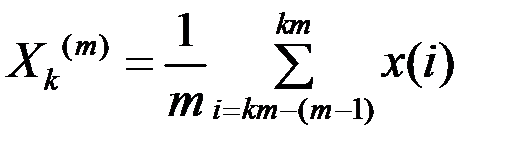 (8.3)
(8.3)
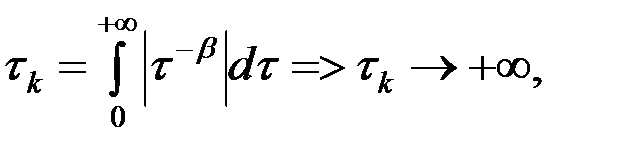 (8.4)
(8.4)
где 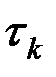 – интервал кореляции.
– интервал кореляции.
Долгосрочная зависимость самоподобных процессов. Процесс 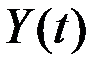 характеризуется долгосрочной зависимостью, если его автокорреляционная функция или функция спектральной плотность мощности спадают асимптотически.
характеризуется долгосрочной зависимостью, если его автокорреляционная функция или функция спектральной плотность мощности спадают асимптотически.
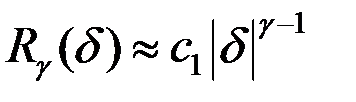 при
при 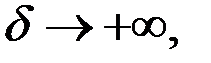
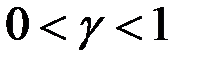 (8.5)
(8.5)
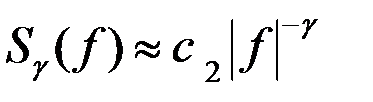 при
при 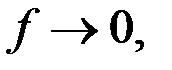
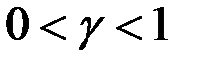 (8.6)
(8.6)
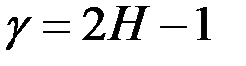 (8.7)
(8.7)
Распределения с «тяжелыми хвостами» (рис. 8.5). Случайная величина 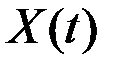 с функцией распределения
с функцией распределения 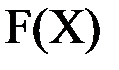 имеет распределение с тяжелым хвостом с индексом хвоста
имеет распределение с тяжелым хвостом с индексом хвоста  , если выполняется условие
, если выполняется условие
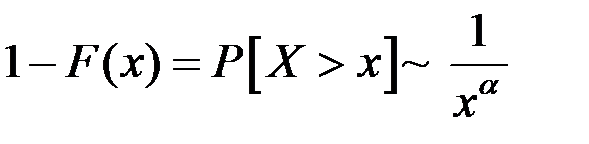 (8.8)
(8.8)
при 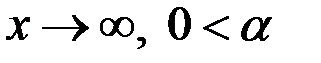 .
.
Рисунок 8.5 – Примеры распределений с «тяжелыми хвостами»
Дата добавления: 2016-06-24; просмотров: 1311;
