Лекция 7. Подходы к моделированию элементов в ТКС
Свойства систем. Среди систем и их моделей встречаются сложные и относительно простые. Сложные системы обладают множеством свойств и соответствующим множеством моделей. Очевидно то, что для сложной системы не существует одной общей модели, которая может быть ее определением. Все свойства систем могут быть разделены на три главных класса:
- общесистемные (целостность, эмерджентность, устойчивость, инвариантность, наблюдаемость, управляемость, открытость, динамичность, надежность и др.);
- структурные (состав, связность, сложность, иерархичность, масштабность, централизованность и др.);
- функциональные, т.е. бихейворальные, поведенческие: инерционность, производительность, оперативность, результативность, точность, экономичность, и др.
Телекоммуникационные системы (ТКС) являются классическим примером сложных организационно-технических систем, определяемых как «множество взаимосвязанных элементов». Здесь выполняется такое важное свойство систем, как целенаправленность. Целенаправленность в ТКС задается выбранными критериями качества предоставляемых услуг (Quality of Service, QoS) и качества функционирования отдельных элементов и всей системы в целом. Выбор адекватных критериев для целенаправленных управляемых систем является важным этапом как при проектировании, так при функционировании систем.
Благодаря реализации управления, на различных уровнях в ТКС обеспечивается эффективное и устойчивое функционирование. В ТКС используются как ситуационные методы управления с помощью лиц, принимающих решения (ЛПР), так и автоматические, реализуемые часто как оптимальные, удовлетворяющие выбранным критериям.
Несмотря на наличие достаточно общих концепций управления типа TMN, TINA и др., до настоящего времени единой для всей ТКС системы управления не создано. На уровнях сетевых элементов, сети, предоставления услуг, бизнес-процессов часто используются независимые, автономные алгоритмы управления, функционирующие по различным критериям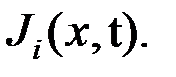 
Для управления функциональными характеристиками систем используются гомеостатические модели, представляемые обычно дифференциальными или разностными уравнениями. Для управления структурными свойствами используют морфогенетические модели в виде различных графов, симплексов, тензорных конструкций и др.
На практике встречаются однокритериальные и многокритериальные задачи. Решения таких задач могут быть ориентированы на получение неких экстремальных, оптимальных свойств системы или на достижение необходимого, требуемого уровня качества этой системы, то есть для системы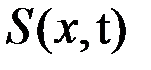 
могут быть выбраны два типа решений:
- оптимальное, когда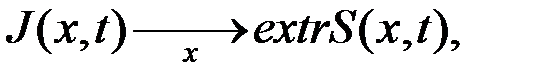 
- достижимое, когда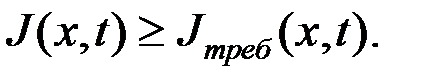 
Решения задач по выбранным критериям могут быть:
- одношаговыми, когда необходимо найти такие параметры, характеристики и ограничения, при которых система 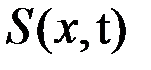обретает нужные свойства (оптимальности или достижимости);
- многошаговыми, которые в свою очередь разделяются на терминальные, когда нужные свойства системы достигаются на конечном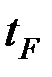 
отрезке времени 
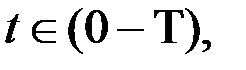и на решения с открытым концом, когда 
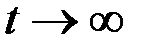и на каждом очередном шаге вдоль траектории движения системы 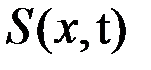поддерживаются требуемые свойства.
Для линейных стационарных динамических систем используют два основных метода представлений:
- представление модели управляемой системы 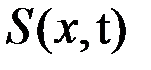в виде передаточной функции 
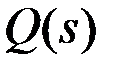в частотной области и исследование реакции этой системы на те или иные воздействия;
- представление модели данной системы во временной области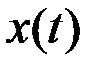 
с помощью уравнения состояния, что дает возможность исследовать непосредственно алгоритм функционирования при различных вариантах его реализации (фильтр, интерполятор, экстраполятор), в том числе и в нестационарных условиях.
Математические модели управляемых систем в частотной области. Известно, что все физически реализуемые сигналы могут быть преобразованы по Лапласу:
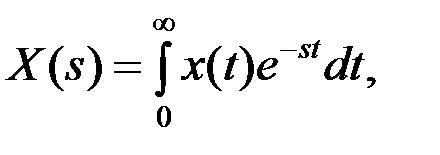(7.1)
где
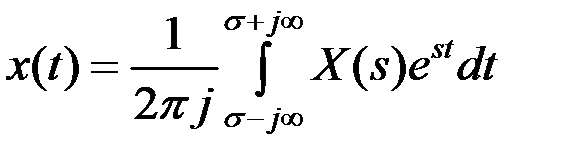
(7.2)
Выражения (7.1) и (7.2) называют прямым и обратным преобразованиями Лапласа. Очевидно, что эти преобразования являются обобщением известных преобразований Фурье. Переменная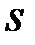 
может рассматриваться как оператор дифференцирования:
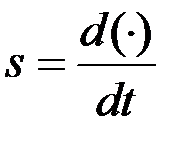(7.3)
Аналогично вводится оператор интегрирования:
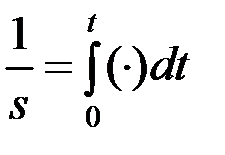(7.4)
Таким образом, дифференциальное или интегро-дифференциальное уравнение удается преобразовать в алгебраическое, что существенно упрощает его решение. Раскладывая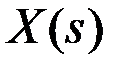 
на простые дроби с помощью правила Хевисайда, находят корни характеристического уравнения системы (нули и полюса). Расположение нулей и полюсов на комплексной S-плоскости определяет характер свободного движения системы, что позволяет судить о ее устойчивости, времени реакции и других важных свойствах.
Динамику исследуемой системы однозначно описывает передаточная функция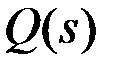 
, определяемая как отношение выходной переменной 
ко входной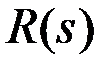 
при условии, что все начальные условия равны нулю:
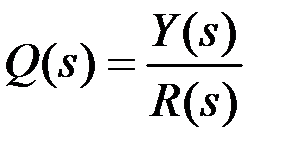(7.5)
Передаточная функция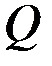 
существует только для линейных стационарных, с постоянными параметрами, систем и не несет никакой информации о внутреннем состоянии и его изменениях. В теории систем такие модели носят название «вход/выход» или «черный ящик».
Ниже приведена характерная модель замкнутой системы с отрицательной обратной связью (рис. 1):
Сигнал на входе объекта 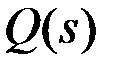представляется в виде:
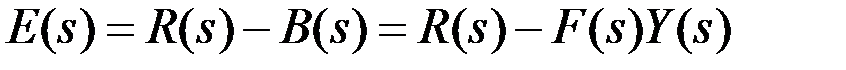(7.6)
Выходной сигнал:
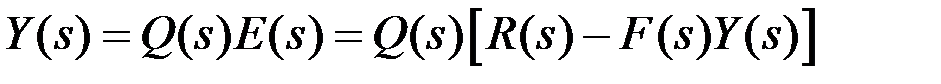(7.7)
Передаточная функция системы:
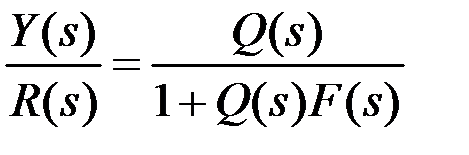(7.8)
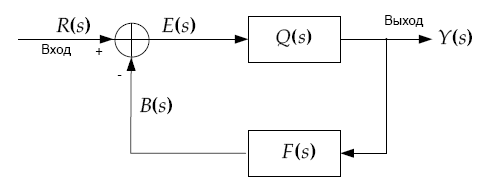
Рисунок 7.1 – Структурная схема системы с отрицательной обратной связью
Таким образом, представление математической модели в частотной области в виде передаточной функции позволяет проводить анализ поведения динамической системы, ее устойчивость и характер реакции, а также осуществлять структурный синтез исходя из взаимодействия отдельных элементов данных систем. Оба рассматриваемые методы представления математических моделей систем в частной и временной областях являются взаимодополняющими. Так, представление во временной области допускает решение как детерминированных, так и стохастических задач анализа и синтеза, в том числе и в нестационарных условиях, а конкретизация внутреннего состояния системы дает возможность непосредственной реализации и исследования эффективных алгоритмов оценки и управления при различных начальных условиях и изменениях параметров.
Цели и задачи моделирования. Целью имитационного моделирования является определение оптимальной структуры и параметров сети.
Основные задачи:
- Определение предельной пропускной способности различных фрагментов сети.
- Определение зависимости потерь пакетов от загрузки отдельных станций внешних каналов.
- Определение времени передачи данных и отклика основных серверов в различных режимах работы.
- Оценка влияния установки новых серверов на перераспределение информационных потоков.
- Оптимизации топологии при возникновении узких мест в сети.
- Выбор того или иного сетевого оборудования, или режима его работы.
- Определение предельно допустимого количества пользователей того или иного сервера.
На рис. 7.2. приведен алгоритм моделирования.
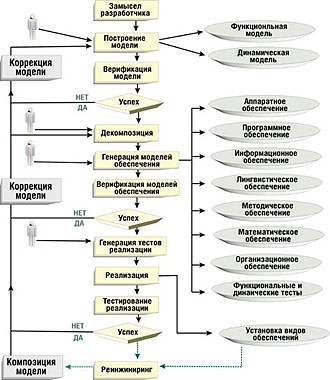
Рисунок 7.2 – Алгоритм моделирования
Исследуемые статистики сетей:
- Статистика очередей: средняя и пиковая длина очереди; СКО очереди.
- Статистика времени ожидания/передачи: среднее и максимальное время ожидания.
- Статистика системного времени: полное число сообщений с статистике системного времени; пиковое значение числа системных сообщений;
- Статистика потерь сообщений: полное число потерянных сообщений; частота потери сообщений; доля потерь из-за переполнения очереди; доля потерь из-за таймаутов.
- Статистика использования ресурсов сети.
Дата добавления: 2016-06-24; просмотров: 775;