Лекция 6. Обработка и анализ результатов моделирования
Условия достижения цели моделирования:
- полученные результаты обладают требуемой точностью и достоверностью;
- исследователь способен правильно интерпретировать полученные результаты и знает, каким образом они могут быть использованы.
Оценка качества моделирования. Оценка качества имитационного моделирования является завершающим этапом разработки модели. Она имеет две цели:
- проверить соответствие модели ее предназначению (целям исследования);
- оценить достоверность и статистические характеристики результатов, получаемых при проведении модельных экспериментов.
При аналитическом моделировании достоверность результатов определяется двумя основными факторами:
- корректным выбором математического аппарата, используемого для описания исследуемой системы;
- методической ошибкой, присущей данному математическому методу.
При имитационном моделировании на достоверность результата влияет положительный ряд дополнительных факторов:
- моделирование случайных факторов, основанное на использовании датчиков случайных чисел, которые могут вносить «искажения» в поведение модели;
- наличие нестационарного режима работы модели;
- использование нескольких разнотипных математических методов в рамках одной модели;
- зависимость результатов моделирования от плана эксперимента;
- необходимость синхронизации работы отдельных компонент модели;
- наличие модели рабочей нагрузки, качество которой зависит, в свою очередь, от тех же факторов.
Калибровка модели.
Если в результате проведенной оценки качества модели оказалось, что ее целевые свойства не удовлетворяют разработчика, необходимо выполнить ее калибровку, т. е. коррекцию с целью приведения в соответствие предъявляемым требованиям.
Как правило, процесс калибровки носит итеративный характер и состоит из трех основных этапов:
1. глобальные изменения модели (например, введение новых процессов, изменение типов событий и т. д.);
2. локальные изменения (в частности, изменение некоторых законов распределения моделируемых случайных величин);
3. изменение специальных параметров, называемых калибровочными.
Целесообразно объединить оценку целевых свойств имитационной модели и ее калибровку в единый процесс.
Процедура калибровки состоит из трех шагов, каждый из которых является итеративным (рис. 6.1).
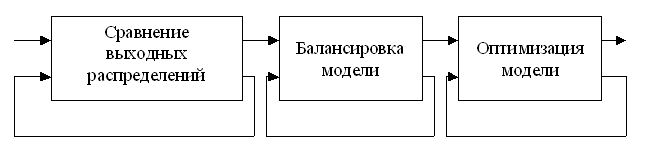
Рисунок 6.1 – Схема процесса калибровки модели
Шаг 1. Сравнение выходных распределений.
Цель — оценка адекватности ИМ. Критерии сравнения могут быть различны. В частности, может использоваться величина разности между средними значениями откликов модели и системы. Устранение различий на этом шаге основано на внесении глобальных изменений.
Шаг 2. Балансировка модели.
Основная задача — оценка устойчивости и чувствительности модели. По его результатам, как правило, производятся локальные изменения (но возможны и глобальные).
Шаг 3. Оптимизация модели.
Цель этого этапа — обеспечение требуемой точности результатов. Здесь возможны три основных направления работ: дополнительная проверка качества датчиков случайных чисел; снижение влияния переходного режима; применение специальных методов понижения дисперсии.
Оценка параметров распределений. Основные критерии проверки гипотез:
1. t-критерий — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Служит для проверки гипотезы о равенстве средних значений двух нормально распределенных случайных величин X и Y в предположении, что дисперсии их равны (хотя и неизвестны). t-статистика строится обычно по следующему общему принципу: в числителе случайная величина с нулевым математическим ожиданием (при выполнении нулевой гипотезы), а в знаменателе — выборочное стандартное отклонение этой случайной величины, получаемое как квадратный корень из несмещенной оценки дисперсии.
2. F-критерий (F-тест, критерий Фишера) — любой статистический критерий, тестовая статистика которого при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение). Служит для проверки гипотезы о равенстве дисперсий Dx и Dy при условии, что х и у распределены нормально. Статистика теста так или иначе сводится к отношению выборочных дисперсий (сумм квадратов, деленных на «степени свободы»). Чтобы статистика имела распределение Фишера необходимо, чтобы числитель и знаменатель были независимыми случайными величинами и соответствующие суммы квадратов имели распределение Хи-квадрат. Кроме того, предполагается, что дисперсия случайных величин, квадраты которых суммируются, одинакова.
3. Критерии согласия — используются для проверки того, удовлетворяет ли рассматриваемая случайная величина данному закону распределения (например, критерий Пирсона).
Оценка влияния и взаимосвязи факторов. Основная задача оценки — отыскание аналитических зависимостей, связывающих между собой различные параметры, фигурирующие в модели. Основные методы:
- Однофакторный дисперсионный анализ.
- Многофакторный дисперсионный анализ.
- Корреляционный и регрессионный анализ.
Однофакторный дисперсионный анализ. Суть анализа сводится к определению влияния на результат моделирования одного выбранного фактора.
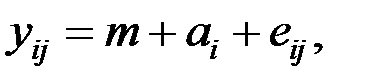 (6.1)
(6.1)
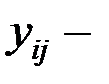 j-е значение у в i-й серии опытов;
j-е значение у в i-й серии опытов;
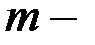 генеральное среднее случайной величины у;
генеральное среднее случайной величины у;
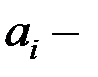 параметр, отражающий влияние фактора х («эффект» i-го значения фактора х);
параметр, отражающий влияние фактора х («эффект» i-го значения фактора х);
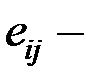 ошибка измерения у.
ошибка измерения у.
Многофакторный дисперсионный анализ (МДА). МДА позволяет выбрать из группы факторов, участвующих в эксперименте, те, которые действительно влияют на его результат.
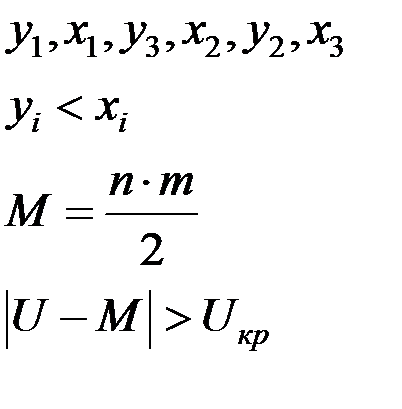 (6.2)
(6.2)
где 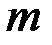 – генеральное среднее случайной величины у;
– генеральное среднее случайной величины у;
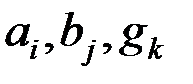 – неизвестные параметры («эффекты» соответствующих факторов).
– неизвестные параметры («эффекты» соответствующих факторов).
Решение задачи дисперсионного анализа заключается в проверке гипотез о независимости результатов измерений от факторов а, b, g:
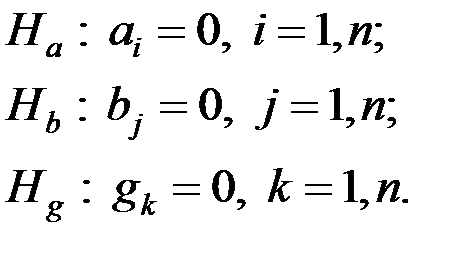
Дата добавления: 2016-06-24; просмотров: 1711;
