Преобразование схем замещения. Коэффициенты распределения токов.

Ответ:После составления схемы замещения, определения сопротивлений всех элементов и приведения этих сопротивлений к одной ступени трансформации схема преобразуется к простому виду, показанному на рис. 2.7.

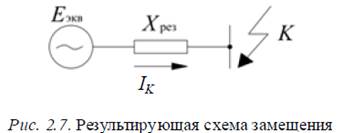
Для преобразования схем используются методы, известные из курса ТОЭ. Так, последовательные сопротивления непосредственно суммируются, параллельные – суммируются через проводимости, производится преобразование треугольника в звезду, трехлучевой звезды в треугольник, замена нескольких источников одним эквивалентным и т. д. При преобразованиях схем в ходе выполнения расчетов нужно учитывать некоторые специфические особенности: 1. Первоочередной задачей расчета КЗ является нахождение тока непосредственно в аварийной ветви или в месте КЗ. Поэтому преобразование схемы нужно вести так, чтобы аварийная ветвь по возможности была сохранена до конца преобразования или, в крайнем случае, участвовала в нем на последних этапах. 2. Часто схема замещения является симметричной относительно

некоторой промежуточной точки. Использование этого обстоятельства позволяет значительно упростить преобразование схемы. Например, если в представленной на рис. 2.8, а схеме параметры Т1 и Т2, G1 и G2 одинаковы, то потенциалы точек А и В одинаковы, поэтому точки А и В можно либо закоротить, либо разорвать.

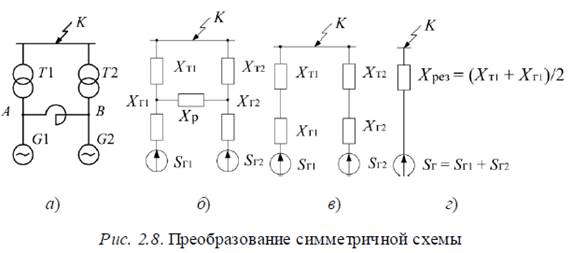3. Замена двух и более однотипных источников питания одним эквивалентным возможна, если источники питания находятся в практически одинаковых условиях по отношению к точке КЗ, что проверяется по условию 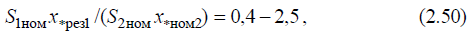где – номинальные мощности источников питания; 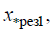– результирующие сопротивления между соответствующим источником питания и точкой КЗ. Если расчетное сопротивление ветви между источником питания и точкой КЗ 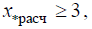то объединение источников питания допустимо при наличии в схеме ветвей, содержащих источник бесконечной мощности (U = const) и источник сопротивления ветви 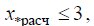объединять их в один эквивалентный источник не рекомендуется, так как при этом ухудшается точность определения тока КЗ. При упрощении схемы замещения ЭЭС можно пренебречь источником меньшей мощности, если

где 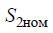– мощность источника питания, меньшего по мощности; –сопротивление цепи между этим источником и точкой КЗ. 4. Коэффициенты распределения токов. В практике расчетов токов КЗ часто возникает необходимость в определении взаимных сопротивлений между точкой КЗ и отдельными источниками. Для этой цели используются коэффициенты распределения. Рассмотрим случай, когда два источника связаны с точкой КЗ через общее сопротивление X3 (рис. 2.9).

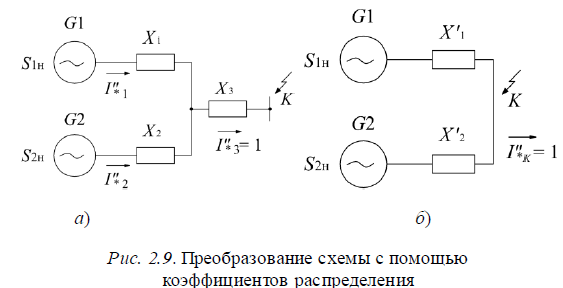Для получения схемы рис. 2.9, б необходимо: а)определить результирующее сопротивление из схемы, приведенной на рис. 2.9, а:

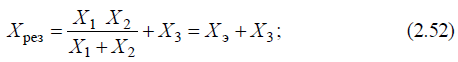б)принять относительное значение сверхпереходного тока КЗ в точке K равным 1, т. е. 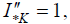откуда в соответствии с законами Кирхгофа можно записать уравнения: 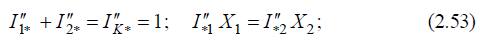в)совместно решая (2.52) и (2.53), находим:

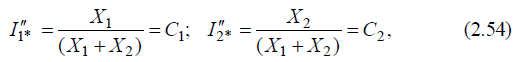где С1 и С2 – коэффициенты распределения, т. е. относительные значения токов КЗ, которыми каждый генератор участвует в питании точки КЗ. Коэффициенты С1 и С2 могут быть определены следующим образом: 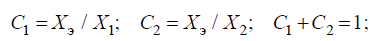г)для замены схемы на рис. 2.9, а схемой на рис. 2.9, б необходимо соблюсти условия: 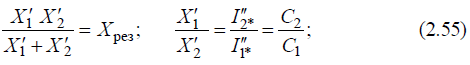д)решая совместно (2.55), получим: 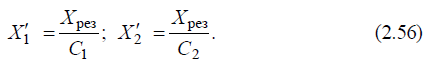Если к точке короткого замыкания через общее сопротивление Хо присоединены n источников, то расчет производится в следующей последовательности:

а)определяются эквивалентное и результирующее сопротивления:

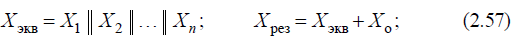б)определяются коэффициенты токораспределения:

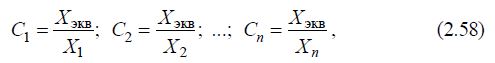причем 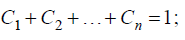в)рассчитываются сопротивления новой схемы замещения: 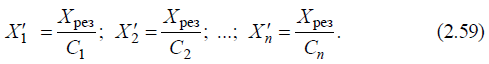Трудность преобразования схем замещения в значительной степени определяется выбранным порядком выполнения операций по упрощению схемы. Поэтому при преобразовании схем следует придерживаться такого порядка расчетов и записи результатов, которые обеспечивают простую проверку получаемых результатов. После получения простейшей схемы (рис. 2.7), содержащей место КЗ и эквивалентную ЭДС за эквивалентным сопротивлением для расчета тока в месте КЗ, используют закон Ома, а для определения токов и напряжений в других ветвях схемы (если в этом есть необходимость) совершают обратный переход – от простейшей схемы к более сложной, вплоть до исходной.