Учёт нагрузки при определении токов КЗ в установившемся и сверхпереходном режимах. Учёт сопротивления дуги в месте КЗ.

Ответ:Расчетные сопротивления линий. Для воздушных и кабельных линий из цветных металлов активное сопротивление проще всего определить по справочным данным. Пользоваться для определения активного сопротивления R выражением 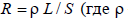– удельное

сопротивление проводника; L и S – его длина, м, и сечение, мм²) не рекомендуется, так как действительное сечение проводов отличается от номинального сечения (прил. 1, табл. П.1.1, П.1.3, П.1.4), действительная длина проволок, из которых свивается провод, за счет скрутки больше длины отдельных проводников. Индуктивное сопротивление воздушных линий для частоты f =50 Гц и магнитной проницаемости м=1 определяется по уравнению

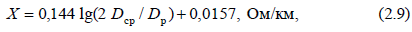где Dр – расчетный диаметр провода, зависящий от числа и сечения отдельных проволок, из которых свивается провод. Величина Dр дается в приложении 1. Величина среднего расчетного расстояния между проводами определяется по выражению 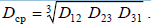Величины D12 , D23, D31 определяются по чертежам опор. Так как расстояния между проводами обычно разные и индуктивные сопротивления трех разных фаз будут не одинаковы, то в распределительных сетях транспозиция фазных проводов не применяется. Индуктивные сопротивления кабелей рассчитать сложно и конструкции их различны. Поэтому активные и индуктивные сопротивления кабелей лучше выбирать по справочным или каталожным данным (прил. 1). Окружающая температура зависит от времени года, времени суток. Кроме того, температура самого провода обычно выше температуры окружающего воздуха за счет подогрева провода током нагрузки, а при отключении КЗ с большой выдержкой времени сопротивление возрастает от нагрева током КЗ. Учет всех этих зависимостей вызывает трудности, поэтому активные сопротивления условно рассчитываются при температуре 20 ºC или максимальной длительно допустимой для данной конструкции. Стальные провода. Активное сопротивление стальных проводов зависит от конструкции провода и значения протекающего по нему тока. Зависимость эта сложная и математическому расчету не поддается. Поэтому активное сопротивление стальных проводов определяется по справочным данным. В приложении 1 приведены зависимости активного, индуктивного и полного сопротивлений стальных проводов от плотности тока. Расчет тока КЗ на линиях со стальными проводами выполняется методом последовательных приближений. Предварительно задаются ожидаемым током КЗ, для этого значения определяют активные и внутренние индуктивные сопротивления проводов. По Dср определяют внешнее индуктивное сопротивление и по этим данным рассчитывают ток КЗ. Полученное значение тока КЗ сравнивают со значением, для которого определились сопротивления. Если разница не превышает 10 %, расчет заканчивается. Если разница велика, расчет повторяется, причем сопротивления определяют для нового значения тока КЗ. Так поступают до тех пор, пока результаты совпадут с точностью до 10 % значения токов. Таким образом, особенностью стальных проводов является низкая удельная проводимость и нелинейная зависимость проводимости от тока, на которую влияет плотность тока и отношение периметра к сечению. Проводимость возрастает с увеличением плотности тока, А/мм², и имеет

относительно большие значения с увеличением отношения периметра к сечению. Провода, кабели и шины. Активное сопротивление проводов, кабелей и шин, выполненных из алюминия, меди, зависит от температуры окружающего воздуха и при повышении температуры увеличивается. Это увеличение описывается уравнением 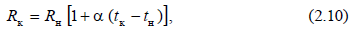где Rн – сопротивление провода при начальной температуре tн ; Rк –cопротивление провода при конечной температуре tк ; a – температурный коэффициент, равный для меди 0,0041 1/ºC, для алюминия – 0,0044 1/ºC и для стали – 0,006 1/ºC. Расчетные сопротивления проводов, кабелей и шин рекомендуется определять по следующей методике. 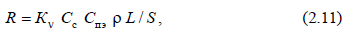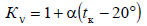Активное сопротивление проводов где – коэффициент увеличения сопротивления с повышением температуры. Коэффициент 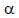определяется по рекомендациям к формуле (2.10). Значения 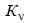для различных температур приведены в табл. 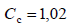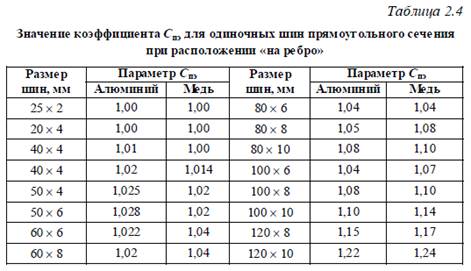2.3; – коэффициент, учитывающий увеличение сопротивления многопроволочных жил проводов и кабелей за счет повива. Для шин и однопроволочных проводов 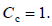Значения Cпэ для медных и алюминиевых шин прямоугольного сечения приводятся в табл. 2.4. Значения коэффициента Cпэ для пакетов шин для приближенных расчетов допустимо принимать как для одиночных шин; 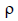– удельное сопротивление при t = 20 ºС: - для меди 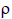= 0,0178 Ом * мм2/м – провода и шины; - для алюминия 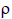= 0,0294 Ом · мм²/м – провода и кабели; - для алюминия 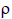= 0,0225 Ом · мм²/м – шины. Сопротивления рассчитывают при следующих температурах: - для проводов и кабелей с резиновой и пластмассовой изоляцией – +65 ºС; - для шин – +70 ºС; - для кабелей с бумажной изоляцией – +80 ºС. 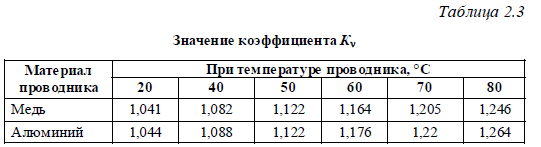Следует отметить, что температура нулевой жилы может быть меньше, чем фазной. Подобное допущение создает некоторый запас при расчетах.

В приложениях 1–3 приводятся значения активных сопротивлений медных и алюминиевых проводов и шин и конструкционных материалов. Если нулевой провод круглый, но отличается от фазного площадью сечения, необходимо индуктивное сопротивление рассчитывать по проводу меньшего сечения. При плоском нулевом проводнике сопротивление определяется по сечению фазного проводника.

Сопротивление электрической дуги. Обычно в месте КЗ образуется некоторое переходное сопротивление, состоящее из сопротивления возникшей электрической дуги и сопротивлений прочих элементов пути токов КЗ от одной фазы к другой или от фазы на землю. Точный учет переходного сопротивления практически невозможен, прежде всего вследствие трудности надежной оценки сопротивления дуги, которое, являясь функцией тока и длины дуги, изменяется в широких пределах. Учет электрической дуги в месте КЗ рекомендуется производить введением в расчетную схему активного сопротивления дуги Rд. Экспериментальные исследования открытых дуг показали, что при токах КЗ в сотни ампер и выше градиент напряжения в дуге мало зависит от тока. При этом сопротивление дуги, являющееся практически активным, определяется по выражению 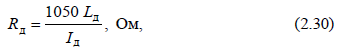где Lд – длина дуги, м; Iд – действующее значение тока в дуге, А. Так, при длине дуги 0,1 м и токе равном 1000 А, сопротивление дуги равно Rд = 0,105 Ом. В ряде случаев переходные сопротивления могут быть столь малы, что практически ими можно пренебречь. Такие замыкания называются металлическими. Естественно, при прочих равных условиях ток при металлическом КЗ больше, чем при наличии переходного сопротивления. Поэтому, когда требуется найти возможные наибольшие величины токов, исходят из наиболее тяжелых условий, считая, что в месте КЗ отсутствуют какие-либо переходные сопротивления. Расчет максимальных и минимальных значений тока дугового КЗ рекомендуется выполнять на основе предельных значений сопротивления дуги, определяемых по статистическим характеристикам разброса поправочного коэффициента, учитывающего снижение тока дугового КЗ по сравнению с током металлического КЗ. При определении минимального значения тока КЗ в установках напряжением до 1000 В следует учитывать влияние на ток КЗ активного сопротивления электрической дуги в месте КЗ. Приближенные значения активного сопротивления дуги приведены в табл. 2.7.

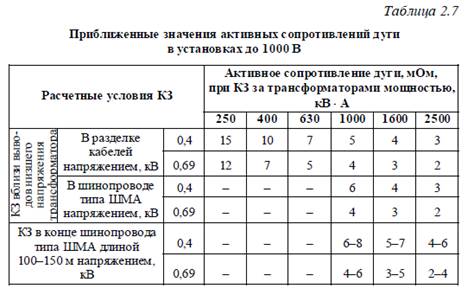В практических расчетах применяются еще две формулы для определения активного сопротивления дуги: 1. Среднее значение активного сопротивления дуги в начальный момент КЗ допустимо определять по формул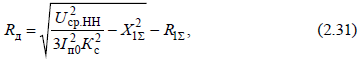е где 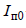Iп0– начальное значение периодической составляющей тока в месте металлического КЗ, кА; 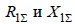– соответственно суммарное индуктивное и суммарное активное сопротивления цепи КЗ, мОм; Кс – сред-

нестатистическое значение поправочного коэффициента, учитывающего снижение тока в начальный момент дугового КЗ по сравнению с током металлического КЗ, который можно определить по формуле 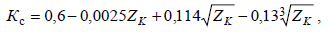где ZK – сопротивление цепи КЗ, зависящее от вида КЗ. При трехфазном КЗ 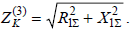2. При точных расчетах активное сопротивление дуги зависит от тока КЗ и длины дуги и рассчитывается по формуле