Определение зависимой и независимых переменных; 6 страница
Завершающий этап процесса кодирования состоит в подготовке книги кодов, которая содержит общие инструкции, указывающие, каким образом была закодирована каждая позиция данных. В ней перечисляются коды каждой переменной и категории, включенные в каждый код. Далее в ней указывается, где в компьютерной записи располагается переменная и каким образом эта переменная читается — например с десятичной точкой или как целое число. Последняя информация обеспечивается установлением формата.
Тема 10: Описательный анализ. Базовые методы анализа маркетинговой информации
1. Построение частотных распределений;
2. Проверка гипотез. Кросс-табулирование.
Данные, полученные в результате исследования и подготовленные к обработке, подвергаются базовому анализу, который содержит следующие этапы:
1. построение частотных распределений (frequency distribution);
2. кросс-табулирование (cross tabulation);
3. проверка гипотез о связях и различиях.
Построение вариационного ряда (частотных распределений)
(frequency distribution)
Так как в матрице ответов содержится значительное число ответов респондентов, то получить обобщенную характеристику возможно построив таблицу одномерного частотного распределения.
С помощью распределения частот можно получить следующие ответы:
ü сколько потребителей знакомо с новым товарным предложением?
ü каково распределение доходов людей, пользующихся торговой маркой?
ü какой процент от общего числа покупателей использует купоны?
Цель построения вариационного ряда (распределения частот) – подсчет и изучение количества ответов, соответствующих различным значениям переменных.
Производится по следующему алгоритму:
1) подсчет числа случаев по каждому значению переменной (табулирование);
Частотное распределение переменной представляют в виде таблицы, где указана частота, частости и накопленные частости, которые принимает изучаемая переменная.
2) расчет процентов и накопленных процентов для каждого значения признака, корректировка на пропущенные значения.
Относительная частота – процент или частость (percent, ¦i/n*100%, где n – объем выборки) – доля объектов, обладающих данным значением, в общей численности.
Валидный процент (valid percent) – относительная частота без учета пропущенных значений.
Накопленный процент(Fi, cumulative frequency) представляет собой сумму всех процентов от первого значения признака до того, к которому относится накопленная частота.
3) построение гистограммы частот.
Основная цель – визуальное представление частотного распределения данных, изучение общего представления о форме распределения, выявление скопления значений в определенном диапазоне.
Гистограмма строитсяпо результатам табулирования данных, измеренных по интервальной или относительной шкале. На ней значения переменных представлены вдоль оси X, а абсолютные или относительные частоты этих значений – вдоль оси Y.
Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить отрезками прямых.
На основе гистограммы оценивают, являются ли данные нормально распределенными.
Кривая нормального распределения – это теоретическая модель, представляющая абсолютно симметричный вид полигона частот. Она имеет форму колокола и одну вершину, а ее концы уходят в бесконечность в обоих направлениях.
В отдельных случаях возможны выбросы данных – сильно отклоняющиеся значения. Иначе называют грубые ошибки. Существует два вида выбросов значений:
– ошибки (их необходимо исправлять);
– корректные, но отличающиеся значения.
4) расчет дескриптивных (описательных) статистик.
Таблица частот представляет собой базовую информацию, ее легко читать, однако иногда возникает необходимость обобщить эту информацию с помощью дескриптивных (описательных) статистик.
К ним относятся:
1. Показатели центра распределения;
2. Показатели вариации (изменчивости);
3. Показатели формы распределения.
1. Показатели центра распределения(measures of location).Характеризуют положение центра распределения, вокруг которого концентрируются данные.
Среднее значение – наиболее распространенный показатель. Его рассчитывают, когда данные относятся к интервальной или относительной шкале. Чаще всего используют среднюю арифметическую.
Мода – значение переменной, которое встречается чаще всего чаще всего. Она соответствует самой высокой точке графика частотного распределения.
Процентили (N-й процентиль) – такое значение переменной, ниже которого расположено N процентов наблюдений данной переменной (сотая доля измерений изучаемой совокупности). Если множество наблюдений разделить на 100 равных частей, то можно получить 99 возможных процентилей.
Первый квартиль – это значение, для которого ¼ или 25% наблюдений находятся ниже него (иначе называют 25% процентиль).
Медиана – значение переменной в середине ряда данных, расположенных в порядке возрастания или убывания. Половина всех объектов из выборки имеют значения переменной, не превосходящие медиану, вторая половина – значения, которые больше, чем медиана.
Положение медианы определяется ее номером. Если количество четное, то она равна полусумме двух серединных значений. Медиана – это 50-й процентиль.
2. Показатели вариации (изменчивости) (measures of variability).Показывают рассеивание (разброс значений) переменной. Дают информацию о степени неоднородности или изменчивости значений внутри распределения:
Размах вариации – это разность между наибольшим и наименьшим значениями переменной в вариационном ряду.
Межквартильный размах – это разность между верхним и нижним квартилями, т.е. 75-м и 25-м процентилями. Эта мера лишена некоторых проблем, характерных для размаха, т.к. рассматривает только средние 50% наблюдений выборки.
Дисперсия (S2x) – это среднее из квадратов отклонений всех значений переменной от ее средней величины. Дисперсия не может быть отрицательной величиной.
Если значения расположены вблизи от среднего – дисперсия невелика; если элементы данных разбросаны – дисперсия существенна. Для выборки дисперсия рассчитывается по формуле:
Стандартное (среднеквадратическое) отклонение (Sx) – это квадратный корень из дисперсии:
Имеет те же единицы измерения, что и исходные данные.
Считается, чем больше значение стандартного отклонения, тем выше изменчивость распределения.
3. Показатели формы распределения.Позволяют судить о том, в какой степени распределение близко к нормальному. Включает показатели:
Асимметрия – показывает, в какую сторону относительно среднего сдвинуто большинство значений распределения. Положительная асимметрия показывает на сдвиг в сторону меньших значений, а отрицательная – в сторону больших значений.
Эксцесс – показатель относительной крутости (островершинности или плосковершинности) кривой вариационного ряда по сравнению с нормальным распределением. При положительном значении – распределение островешинное; при отрицательном – плосковершинное.
Отдельным направлением базового анализа выступает статистическая проверка гипотез.
Статистическая гипотеза – утверждение относительно параметров генеральной совокупности, сформулированное по определенным правилам и подлежащее проверке с помощью выборочного исследования.
Статистические гипотезы служат инструментом проверки выдвигаемых теоретических положений. Бывают двух видов:
ü если предположения делаются относительно параметров статистического распределения (среднего значения или дисперсии) – параметрическая гипотеза;
ü относительно распределения случайной величины (подчинение нормальному распределению, закону Пуассона и др.) – непараметрическая гипотеза.
Общая последовательность проверки гипотез включает следующие этапы:
1. Формулирование гипотез
Статистическая гипотеза состоит из двух утверждений:
Нулевая гипотеза (прямая) – является основной и обычно содержит утверждение об отсутствии различий между сравниваемыми параметрами. Обозначается H0.
Альтернативная гипотеза (обратная) – является противоположной нулевой и принимается после того, как отвергнута основная. Это утверждение, в котором предполагается наличие различий (либо взаимосвязей) между сравниваемыми параметрами.Обозначается H1.
Маркетолог всегда проверяет именно нулевую гипотезу.
2. Выбор подходящего метода проверки гипотезы (статистического критерия).
Статистический критерий – правило, с помощью которого принимаются решения о принятии (отклонении) выдвинутой нулевой гипотезы на основании результатов, наблюдаемых в выборке.
Выбор критерия зависит от цели исследования.
Выбор уровня значимости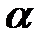 
.
Так как любое решение (принять или отклонить H0) принимается на основе выборки, существует риск получения неверного вывода.
Различают ошибки двух видов:
Ошибка первого рода – возникает, если по результатам выборки отвергается нулевая гипотеза, которая, в действительности, является верной. Вероятность ее появления обозначают 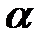и иначе называют уровнем значимости.
Ошибка второго рода – принимается нулевая гипотеза, в то время как она является ошибочной. Вероятность ее появления обозначают 
. А вероятность не совершить такую ошибку 1– – это мощность критерия.
Распространены значения 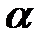: 0,1; 0,05; 0,01. Если 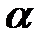=0,01, то исследователь не хочет совершить ошибку первого рода более чем в 10 случаях из 1000. Уровень значимости указывает на вероятность получения достоверного вывода, которая рассчитывается как (1– 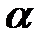), т.е.: 0,90, 0,95, 0,99.
2. Нахождение размера выборки, сбор данных и вычисление выборочной статистики
3. Определение вероятности получения выборочной статистики или критических значений для проверочной величины
Критическое значение – это значение проверочной статистики, которое разделяет области отклонения и принятия нулевой гипотезы.
4. Сопоставление найденной вероятности с уровнем значимости 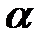или изучение, попадает рассчитанная проверочная статистика в область отклонений или принятия гипотезы.
5. Принятие суждения об истинности или ложности гипотезы Н0.
Если рассчитанная вероятность меньше уровня значимости 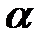, то нулевая гипотеза Н0 отвергается.
Если рассчитанное значение проверочной статистики больше критического значения, то гипотезу Н0 также отклоняется.
8. Формулирование заключения.
Заключение должно быть выражено в контексте проблемы маркетингового исследования и управленческих решений.
К наиболее распространенным методам изучения взаимосвязи двух переменных относятся методы анализа таблиц сопряженности.
Таблицы сопряженности (кросс-табулирование) – это статистический метод объединения распределения значений двух или более переменных одновременно в одну таблицу. Таблицы сопряженности служат для описания связей двух (и более) категориальных переменных. Наиболее распространены таблицы сопряженности с двумя переменными (называют двумерное перекрестное табулирование).
Для оценки взаимосвязи между переменными в таблицах сопряженности используют следующие статистические приёмы:
Статистический критерий хи-квадрат (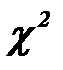 
/хи-квадрат) – критерий согласия Пирсона, который используется для проверки статистической значимости связей, наблюдаемых в таблицах сопряженности.
Недостаток 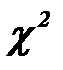: делается вывод о наличии связи, но не даётся ответ о том, какая связь. Это позволяют оценить коэффициент Фишера (фи) и коэффициент сопряженности признаков Пирсона.
Коэффициент Фишера (фи) – используется для измерения связи в таблицах сопряженности, которые состоят из 2 строк и 2 столбцов (размерностью 2Х2).
Этот коэффициент принимает значения от 0 (связи между признаками нет) до 1 (абсолютная взаимосвязь).
Коэффициент сопряженности Пирсона – используется для измерения связи в таблицах сопряженности любого размера. Коэффициент колеблется от 0 (связи между признаками нет) до 1 (никогда не равняется 1). Чем ближе к единице, тем теснее связь.
Тема 11: Дисперсионный и ковариационный анализ
1. Дисперсионный анализ. Процедура выполнения дисперсионного анализа.
2. Ковариационный анализ. Условия применения ковариационного анализа.
Дисперсионный анализ – это статистический метод, при помощи которого исследуется влияние одной или нескольких независимых переменных на одну или несколько зависимых переменных.
Независимая переменная(факторная) – переменная причины, которая определяет изменение другой переменной (результативной). Обозначается х.
Зависимая переменная(результативная) – отражает следствие и зависит от изменения факторных переменных. Обозначается у.
Для наилучшей точности расчетов необходимо соблюдать следующее:
ü Независимая переменная может принимать несколько значений, следовательно при ее помощи можно разделить все единицы на несколько групп (категорий), т.е. это категориальная переменная (номинальная или порядковая).
ü Зависимая переменная является всегда количественной, метрической – т.е. измеряется с помощью интервальной и относительной шкалы.
Различают несколько видов дисперсионного анализа:
1.одномерный дисперсионный анализ. Метод дисперсионного анализа, в котором оценивается один или несколько факторов, влияющих на изменение зависимой переменной.
2.многомерный дисперсионный анализ. При котором исследуется влияние одного или нескольких факторов, влияющих на изменение нескольких зависимых переменных.
Сущность дисперсионного анализа заключается в проверке гипотезы о влиянии независимых переменных на зависимую. В основе техники проведения дисперсионного анализа лежит сравнение средних значений результативного признака в разных группах.
Рассмотрим однофакторный дисперсионный анализ.
Однофакторный дисперсионный анализ проводится с целью определения влияния одной (независимой) переменной на другую (зависимую) переменную.
В результате исследования в зависимости от значений независимой переменной выделяют несколько групп (категорий), для которых рассчитываются средние значения зависимой (результативной) переменной.
Следовательно, нулевая гипотеза формулируется следующим образом: средние величины в различных группах равны, т.е.:
H0: 
Эта гипотеза утверждает, что нет различий во влиянии факторного признака на результативный.
Алгоритм однофакторного дисперсионного анализа включает следующие этапы:
1) Определение зависимой и независимой переменной;
Производится теоретический анализ, в ходе которого устанавливаются зависимые и независимые переменные. Производится сбор данных.
2) Разложение общей дисперсии;
При оценке различий между средними значениями по отдельным группам измеряют вариацию между ними на основе суммы квадратов отклонений.
При этом различают следующие виды суммы квадратов отклонений (вариаций):
Полная (общая) вариация – общая сумма квадратов отклонений значений признака от средней величины.
Она рассчитывается в целом по совокупности и показывает вариацию (колеблемость) результативного признака у, сложившуюся под воздействием всех факторов:
,
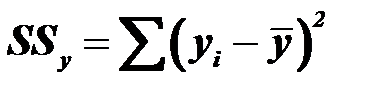где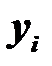 
– индивидуальное значение результативного признака;
– среднее значение по всем единицам (общая средняя).
Согласно модели однофакторного дисперсионного анализа общую вариацию результативной переменной y можно разложить на два компонента.
Общая вариация складывается из двух компонентов:
1) межгрупповой (факторной) вариации;
2) внутригрупповой (остаточной) вариации.
Эту взаимосвязь можно представить следующим образом:
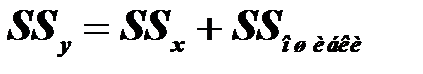
Смысл разложения полной вариации в том, чтобы наглядно представить и затем изучить различия в групповых средних.
Межгрупповая вариация – характеризует колеблемость результативного признака, которая возникает под воздействием только факторного признака х, который положен в основу группировки:
,
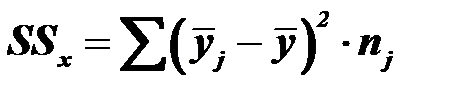где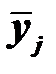 
– среднее значение результативного признака в j-й группе;
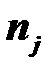– число единиц в j-й группе.
Внутригрупповая вариация (остаточная, ошибки) – измеряет колеблемость результативного признака, связанную с влиянием всех прочих признаков, кроме факторного:
,
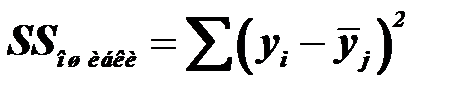где 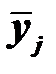– среднее значение результативного признака в j-й группе.
Величина вариации (колеблемости) зависит от числа единиц в группе, поэтому при разной численности групп эти величины будут несопоставимы. Чтобы численность групп не влияла на величину вариации, вычисляют дисперсии в расчёте на одну степень свободы.
Число степеней свободы для разных видов вариации равно:
ü для общей вариации: df общ=n – 1;
ü для межгрупповой дисперсии: df межгр =m – 1;
ü для внутригрупповой дисперсии: df ост =n – m.
Деление сумм квадратов отклонений на соответствующее число степеней свободы дает три вида дисперсии (средний квадрат отклонений):
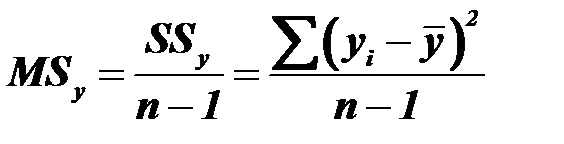- общая дисперсия;
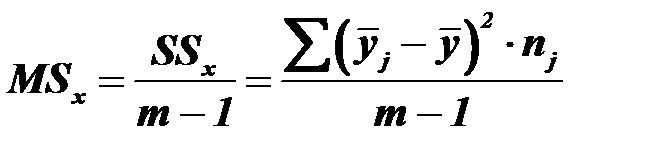- межгрупповая дисперсия;
- внутригрупповая (остаточная, ошибки).
3) Измерение эффектов(исчисление корреляционного отношения);
Степень влияния независимого признака х на результативный у оценивается с помощью корреляционного отношения.
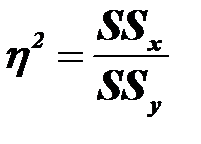
Значение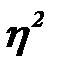 
варьируется от 0 до 1. Оно равно 0, когда все групповые средние равны, т.е. переменная х не влияет на у. Значение 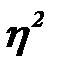равно 1, когда внутри каждой из групп переменной х изменчивость отсутствует, но имеется некоторая изменчивость между группами.
Таким образом, корреляционное отношение показывает долю вариации результативной переменной, обусловленную влиянием факторной (независимой) переменной.
4) Проверка значимости.
Нулевую гипотезу (о равенстве групповых средних) можно проверить с помощью расчета F-критерия:
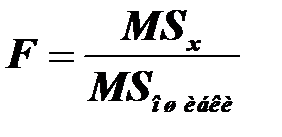
Расчетное значение сравнивают с табличным значением. F-критерий Фишера построен так, что его значение всегда положительно и может изменяться от 1 до бесконечности. Этот критерий подчиняется F – распределению, поэтому рассчитанное значение сопоставляют с табличным при уровне значимости α и числе степеней свободы (df), равным m – 1 и n – m.
Если Fфакт > Fтабл, то нулевая гипотеза отклоняется. Следовательно, влияние признака-фактора является существенным или значимым.
5) Интерпретация полученных результатов.
Если нулевую гипотезу о равенстве групповых средних не отклоняют, то независимые переменные не оказывают статистически значимого влияния на зависимую переменную.
С другой стороны, если нулевую гипотезу не учитывать, то эффекты независимых переменных на зависимую трактуются как статистически значимые. То есть среднее значение зависимой переменной отличается для различных групп независимой переменной. Сравнение значений групповых средних показывает характер влияния независимой переменной.
При многофакторном дисперсионном анализе (ANOVA) исследуется влияние двух и более факторов на одну результативную переменную.
Процедура многофакторного дисперсионного анализа аналогична однофакторному дисперсионному анализу. Многофакторный дисперсионный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее. Здесь кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать их совместное действие.
Основой для проведения такого анализа выступает комбинационная группировка (ее производят по двум и более признакам).
При таком анализе необходимо учитывать взаимодействия между факторами, причем с возрастанием числа факторов существенно нарастает сложность интерпретации взаимодействий.
Взаимодействие двух факторов означает, что влияние одного из них проявляется по-разному на разных уровнях другого фактора.
Статистические характеристики, соответствующие многофакторному дисперсионному анализу, также определяются по аналогии с однофакторным дисперсионным анализом.
Если проводится исследование, в котором участвует и метрические независимые переменные и категориальные, то используют ковариационный анализ.
Ковариационный анализ – это специальный метод анализа дисперсий, в котором эффекты (влияние) одной или более независимых переменных, выраженных в метрической шкале, удаляют из зависимой переменной перед выполнением дисперсионного анализа.
Ковариационный анализ используют при проверке взаимосвязей зависимой переменной с одной контролируемой и неконтролируемыми независимыми переменными.
Ковариационный анализ является как бы синтезом регрессионного и дисперсионного анализа. Основные теоретические и прикладные проблемы ковариационного анализа относятся к линейным моделям. Если в линейной модели взаимосвязи присутствуют только категориальные предикторы с помощью введения фиктивных переменных, то получается модель дисперсионного анализа. Если в линейной модели присутствуют только количественные предикторы – получается модель регрессионного анализа. А при совместном введении факторов и ковариат проводится ковариационный анализ.
Ковариата – количественная независимая переменная, используемая в ковариационном анализе, значительно коррелирующая с зависимой переменной. Она может быть выражена в метрическом виде (т.е. в виде относительной или интервальной шкалы). По отношению к зависимой переменной ковариаты являются сопутствующими переменными.
Основные этапы реализации ковариационного анализа идентичны этапам дисперсионного анализа. Имеются следующие особенности (принципы).
Принципы (особенности) ковариационного анализа:
ü по смыслу включение в анализ ковариаты означает исключение ее влияния на зависимую переменную.
За счет этого вариация последней уменьшается, что позволяет сделать более очевидным влияние анализируемых факторов;
ü вариацию в зависимой переменной, обусловленную ковариатой, удаляют путем корректировки среднего значения зависимой переменной.
На основе скорректированных значений выполняют дисперсионный анализ;
ü значимость суммарного эффекта и эффекта каждой ковариаты оценивают с помощью F-критерия (отношение межгрупповой дисперсии к дисперсии ошибки).
Тема 11: Корреляционно-регрессионный анализ
1. Характеристика и задачи корреляционно-регрессионного анализа.
2. Корреляционный анализ. Диаграмма рассеяния. Интерпретация коэффициента корреляции.
3. Регрессионный анализ. Уравнение регрессии. Стандартная ошибка оценки. Коэффициент детерминации.
Корреляционный и регрессионный анализ применяются для обозначения методов, направленных на изучение связи между двумя или более переменными, измеренными по интервальной или относительной шкале.
Если при изменении значений одной переменной меняется распределение другой переменной, то между двумя переменными существует статистическая связь.
С помощью корреляционно-регрессионного анализа решают следующие задачи:
1) измерение тесноты связи между двумя (и более) переменными;
2) изучение направления взаимосвязи;
3) оценка параметров уравнения регрессии;
4) проверка значимости построенной модели и др.
Он направлен на установление степени связи (корреляционный анализ), а также её формы, т.е. аналитического выражения, связывающего признаки (регрессионный анализ).
Несмотря на то, что корреляционный и регрессионный анализ очень часто заменяют и дополняют друг друга, существуют различия в целях их применения.
Корреляционный анализ – метод, используемый для измерения степени связи между двумя или более переменными. При этом он рассматривает совместное изменение двух оцениваемых переменных.
Регрессионный анализ – метод, используемый для построения уравнения регрессии, которое описывает связь зависимой переменной с двумя или более независимыми переменными. Этот метод позволяет исследовать распределение зависимой переменной в условиях, когда одна или несколько независимых переменных сохраняются фиксированными на различных уровнях.
Т.е. фактически оба метода изучают одну и ту же взаимосвязь, но с разных сторон, и дополняют друг друга. На практике корреляционный анализ выполняется перед регрессионным анализом. После доказательства наличия взаимосвязи методом корреляционного анализа можно выразить форму этой связи с помощью регрессионного анализа.
Дата добавления: 2016-06-13; просмотров: 4534;