АВТОМАТОВ И АВТОМАТИЧЕСКИХ ЛИНИЙ

При смешанном агрегатировании одновременно имеет место параллельное и последовательное расположение рабочих позиций. Очевидно, как это следует из названия, что при смешанном агрегатировании может иметь место последовательное расположение машин с параллельным агрегатированием или параллельное расположение машин с последовательным агрегатированием. На самом деле такое деление не принципиально, поскольку оно условно. Ведь важно в данном случае лишь то, что в одной машине или линии имеется много позиций, на которых выполняются одинаковые и различные операции. Разумеется, что такое оборудование имеет все недостатки и достоинства, которые характерны для параллельного и последовательного агрегатирования. Однако, можно предположить, что в данном случае проблема выбора числа позиций имеет особую остроту.

Рассмотрим модель машины, состоящей из p параллельно объединенных машин с последовательным агрегатированием и имеющих по q позиций. Производительность машины с параллельным агрегатированием Q(p) определяется формулой:

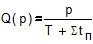, (1)

где p - число параллельных потоков, 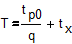- время технологического цикла линии с последовательным агрегатированием, 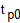- время, необходимое на реализацию техпроцесса каждой детали, q - число последовательно расположенных позиций, 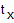- время холостого хода ( в дальнейшем будем считать, что время холостого хода не зависит от числа позиций), 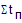- суммарные внецикловые потери. Внецикловые потери 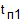для одного потока могут быть представлены в виде:

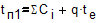, (2)

где - потери по одному комплекту инструмента, - потери по одному комплекту механизмов. Поскольку все потоки объединены, то суммарные потери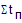

составят: 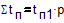. (3)

Учитывая, что технологическая производительность 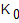- величина обратно пропорциональная технологическому времени 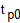, и подставляя последовательно (2) в (3), а (3) в (1), получим:

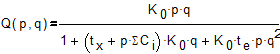. (4)

Это наиболее общая формула, которая может быть использована как для параллельного агрегатирования (q=1) , так и для последовательного агрегатирования (p=1). Для исследования производительности рассмотрим (4) как параметрическую формулу с параметром p. При 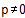справедливы следующие выражения:

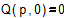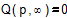и . (5)

Из (5) следует, что производительность Q(p,q) имеет экстремум, поскольку её значения положительны при любых положительных значениях параметров, входящих в (4). Для нахождения экстремума продифференцируем (4) по q:

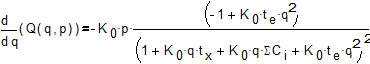. (6)

Приравнивая правую часть (6) нулю и разрешая полученное уравнение относительно q, получим:

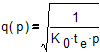. (7)

Число параллельных потоков выступает здесь в качестве параметра. Рассмотрим зависимость q(p) при = 0.002 1/c и 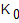= 0.6 с (см. рис.1). Из графика видно, что с увеличением числа параллельных потоков оптимальное число последовательных позиций уменьшается. Причем эта зависимость имеет непропорциональный характер.

Подставляя (7) в (4), можно получить зависимость максимально достижимой производительности 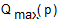при заданном числе параллельных потоков p :

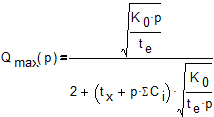. (8)

На рис.1 представлена функция 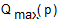при фиксированных значениях остальных параметров.

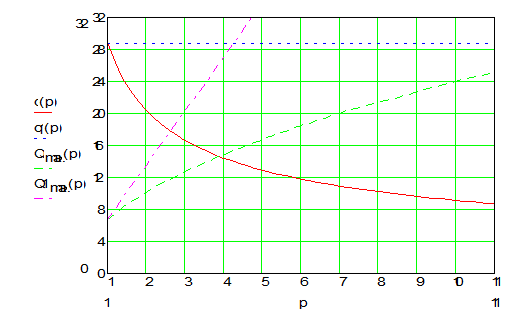
Рис.1. Зависимость оптимального числа позиций и максимально достижимой

производительности при tx=0.03 c, te=0.002c, =0.002 c и Ko=0.6 c

Очевидно, что функция имеет предел. Для его нахождения достаточно числитель и знаменатель разделить на 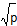и далее воспользоваться правилом нахождения предела от частного:

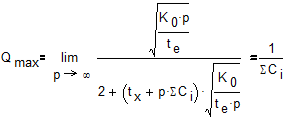. (9)

Из (9) следует, что при любом сколь угодно большом увеличении числа последовательных позиций q и числа параллельных потоков p производительность машины или линии имеет предел, который численно обратно пропорционален потерям по комплекту инструмента. Это обстоятельство объясняется тем, что компенсировать можно любые потери за исключением потерь на регулировку, смену или ремонт инструмента.

На рис.2 представлены зависимости производительности машины или линии со смешанным агрегатированием от числа последовательных позиций q при различном числе параллельных потоков p, tx=0.03 c, te=0.002 c, =0.002 c и Ko=0.6 c, построенные на основании выражения (4).

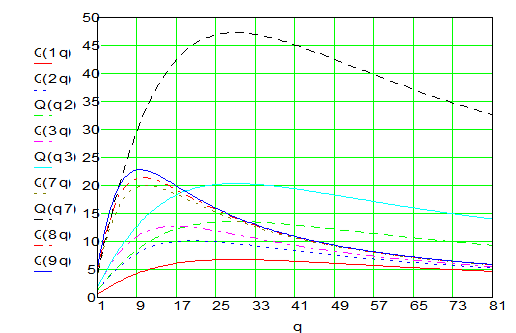
Рис. 2. Производительность машины с параллельным агрегатированием при

различном числе последовательных позиций и параллельных потоков

Из графиков, представленных на рис. 2, следует, что при большом числе параллельных потоков производительность очень критична к числу последовательных операций в каждом потоке.

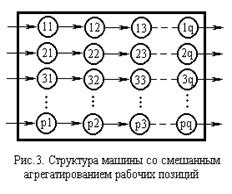
Схема смешанного агрегатирования представлена на рис.3. Машина, выполненная по такой схеме, имеет p параллельных потоков и q последовательных позиций в каждом потоке. Конструктивно схему можно выполнить несколькими способами. Наиболее простым из них является многорядное расположение позиций. Кроме того, позиции часто располагаются по окружности. Сами позиции в таких машинах неподвижны. Недостатки этих схем заключаются в необходимости дублирования всех механизмов (в том числе питания) и выдаче продукции одновременно на нескольких позициях.

Рассмотрим конкретные примеры линий со смешанным агрегатированием. На рис.4 представлена схема роторной линии .

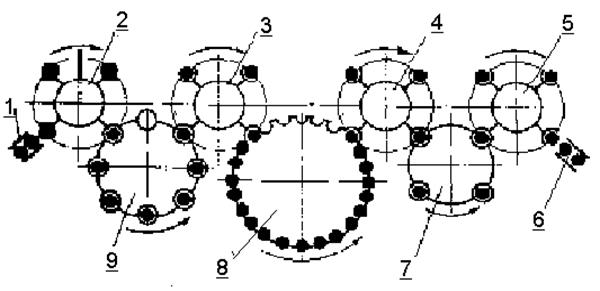
Рис.4. Схема роторной линии

Загрузка роторной линии осуществляется из магазина накопителя 1, транспортирование изделий внутри машины производится транспортными роторами 2, 3, 4 и 5, а разгрузка осуществляется в приемный магазин 6. Технологические роторы 7, 8 и 9 имеют разное число позиций. В представленной машине (линии) три машины с параллельным агрегатированием рабочих позиций соединены последовательно транспортными роторами. Главной особенностью таких машин и линий является то, что технологические роторы могут иметь различное число рабочих позиций.

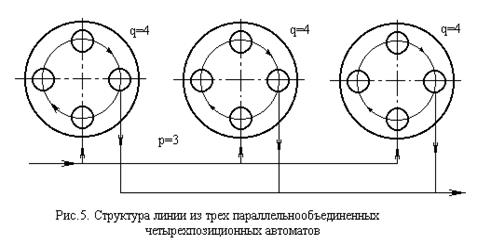
На рис. 5 представлена схема линии с параллельным агрегатированием, состоящей из трех четырехпозиционных машин последовательного агрегатирования. Особенностью такой схемы является то, что все три машины должны быть одинаковыми (делать одни и те же операции, а также иметь одинаковое число позиций). Линии, выполненные по схеме, представленной на рис.5, иногда имеют независимые параллельные потоки. В этом случае суммарные потери каждой машины с последовательным агрегатированием независимы от других машин и определяются формулой:

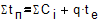. (10)

После подстановки (10) в (1) и соответствующих преобразований выражение для производительности :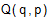

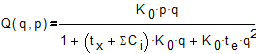. (11)

Для анализа выражения (11) продифференцируем его по q:

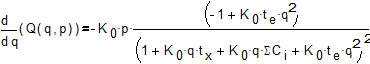. (12)

Из (12) следует, что оптимальное число последовательных позиций q не зависит от числа параллельных потоков p и определяется также, как и при простом последовательном агрегатировании:

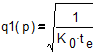. (13)

Подставляя (13) в (12), получим выражение для определения зависимости максимальной производительности от числа параллельных потоков:

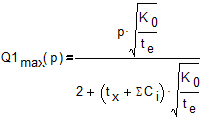. (14)

Для сравнения графики функций, соответствующие выражениям (13) и (14), представим на рис.1. На рис.2 для сравнения приведем кривые производительности, соответствующие выражению (11). Сравнительный анализ показывает, что линии со смешанным агрегатированием, состоящие из p независимых q позиционных последовательно агрегатированных машин, позволяют достичь большей производительности. Однако, такая машина может быть построена, например, по схеме, представленной на рис.5, и никогда не может быть реализована по схеме, изображенной на рис.4.

Машины и линии со смешанным агрегатированием широко применяются для автоматизации простых по реализации технологических операций в массовом производстве. Традиционно они используются для изготовления патронов, в фармацевтической, пищевой (фасовка жидких и сыпучих продуктов) и легкой (изготовление фурнитуры) промышленности .

Вопросы для самоконтроля

1. Каким образом может быть организовано смешанное агрегатирование рабочих позиций?

2. Чем обусловлено наличие оптимального числа позиций оборудования со смешанным агрегатированием?

3. Существует ли ограничение роста производительности оборудования со смешанным агрегатированием при увеличении числа рабочих позиций?

4. От чего зависит оптимальное число последовательных позиций машин, сблокированных параллельно?

5. Приведите примеры применения машин со смешанным агрегатированием.