Нужно решить задачу.

II методика

Пример: определите БРУТТО ставку при страховании имущества юридических лиц на основе страховой статистики за 5 лет с учётом прогнозируемого уровня убыточности страховой суммы на следующий год (при заданной гарантии безопасности 0,9).

Показатели	Годы

Фактическая убыточность страховой суммы (%)	2,8	3,2	3,1	3,4	3,6

Нагрузка в БРУТТО ставке = 22%

Основная часть НЕТТО ставки (То) = ? = прогнозируемый уровень убыточности страховой суммы на следующий за анализируемым периодом год.

Для этого будем использовать модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваем на основе линейного уравнения следующего вида:

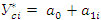
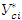- выровненный показатель убыточности страховой суммы

a0 и а1 – параметры линейного тренда

i – порядковый номер соответствующего года

Параметры линейного тренда будем определять методом наименьших квадратов, решав систему уравнений:

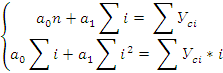
Отсчёт лет ведём с середины ряда, тогда сумма i = 0, а система упрощается:

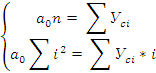
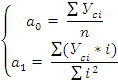
Расчёт параметров уравнений прямой и среднеквадратического отклонения фактических значений убыточности от выровненных, представим след таблицей:

Годы	Фактическая убыточность (Усi), %	Условное обозначение лет (i)	Расчётные показатели	Выровненная убыточность (Ус*i)	Усi – Усi*	(Усi – Усi*)²
Усi * i	I²
	2,8	-2	-5,6		2,86	-0,016	0,0036
	3,2	-1	-3,2		3,04	-0,12	0,0256
	3,1				3,22	-0,02	0,0144
	3,4		3,4		3,4
	3,6		7,2		3,58	0,02	0,0004
					4,3
Итого	16,1		1,8		16,1

Основная часть ставки на следующий год ( 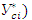= 4,3% от страховой суммы

Определим рисковую надбавку:

Тр=Ϭβ (γ,n)

Ϭ =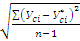

Ϭ – среднеквадратическое отклонение фактических уровней убыточности от выровненных

(в задаче Ϭ = 0,105%)

β – это коэффициент, который зависит от заданной гарантии безопасности гамма (той вероятности, с которой собранных взносов хватит на выплату страховых возмещений) и n (числа анализируемых лет).

n	Γамма
0,8	0,9	0,95	0,975	0,99
	2,972	6,649	13,640	27,448	68,640
	1,592	2,829	4,380	6,455	10,448
	1,184	1,984	2,850	3,854	5,500
	0,980	1,596	2,219	2,889	3,900

Посчитать рисковую надбавку, НЕТТО и БРУТТО ставки. (Тр, Тn, Тб)

Тр = 0,105 * 1,984 = 0,20832%

Тn = 4,3% + 0,208 = 4,508%

Тб = 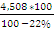= = 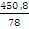5,779%

Расчёт тарифных ставок по методике, предлагаемой статистиками

В этом случае в расчёте нетто-ставки лежит убыточность страховой суммы за период, предшествующий расчётному (обычно за 5 предыдущих лет). Основная часть нетто-ставки (То) = средней убыточности страховой суммы за предшествующий период и определяется как:

То = =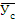

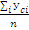
Тр = t * Ϭ

Ϭ – среднеквадратическое отклонение убыточности страховой суммы за предшествующий период.

t – коэффициент доверия зависит от требуемой вероятности, с которой собранных взносов хватит на выплаты возмещений по страховым случаям.

Ϭ =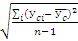

Значение вероятности при разной величине коэффициента доверия (t)

t	Вероятность	t	Вероятность	t	Вероятность
	0,6827		0,9545		0,9973
1,5	0,8664	2,5	0,9876	3,28	0,9990

ПРИМЕР:

По страховой организации сложились след показатели убыточности страховой суммы по добровольному страхованию домашнего имущества граждан.

Показатели	годы

Убыточность страховой суммы (%)	1,2	1,4	1,1	1,5	1,2

Определить:

1) Основную часть НЕТТО-ставки

2) С вероятностью 0,54 – рисковую надбавку

3) НЕТТО и БРУТТО ставку при условии, что нагрузка составляет 26% в БРУТТО-ставке.

ПРИМЕР:

Рассчитайте конечную тарифную ставку по страхованию от несчастных случаев.

Вероятность наступления риска – 0,02

Средняя страховая сумма = 20т.р.

Среднее страховое возмещение = 8000

Количество договоров, которые предполагается заключить со страхователями = 1100

Доля нагрузки в тарифной ставке – 26%

Среднеквадратическое отклонение страхового обеспечения – 2,5 т.р.

Коэффициент зависящий от гарантий безопасности α(γ) – 1,645

<3 4 567 8 9 >

Дата добавления: 2016-05-25; просмотров: 1696;