Уравнения массоотдачи и массопередачи в локальной форме.
Запишем уравнения массоотдачи для двух фаз G и L. В качестве движущих сил используем разность концентраций.
Предположим, что распределяемый компонент переходит из фазы G в фазу L:
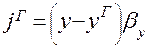(1.15)
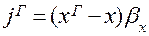(1.16)
где х и у – рабочие концентрации, распределяемого компонента в фазах L и G
соответственно. Используя допущение об отсутствие сопротивления переносу вещества со стороны межфазной поверхности равновесии на границе раздела фаз, запишем:
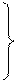
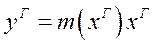(1.17)
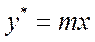
Если коэффициент распределения не зависит от состава фазы то
.
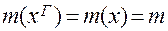Уравнение (1.16) с учетом (1.17) представим в виде:
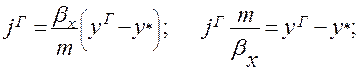
а уравнение (1.15) в виде
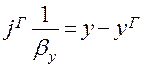
Последние соотношения сложим:
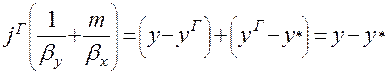
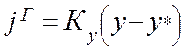(1.18)
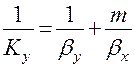или
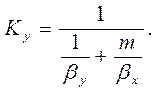(1.19)
Уравнение (1.19) выражает аддитивность фазовых сопротивлений.
Если движущая сила процесса выражается в концентрациях другой фазы L, то уравнение массопередачи примет вид:
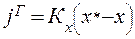(1.20)
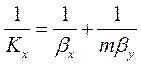
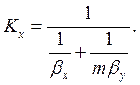(1.19)
Итак, мы получили уравнения массопередачи (1.18) и (1.20), движущими силами в которых являются разности рабочей и равновесной концентрации компонента в одной из фаз. Использование коэффициентов массопередачи Ку или Кх зависит от выбора фазы, через концентрацию, которой записана движущая сила.
Связь между Ку и Кх устанавливается по формулам (1.18) и (1.20) и имеет вид:
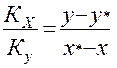(1.22)
В частных случаях, когда m=const получаем:
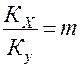
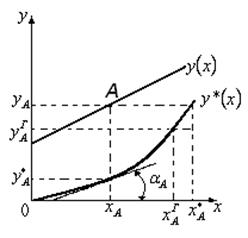
Рис.1.6. Определение коэффициента распределения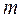 
.
В общем случае зависимость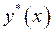 
представляет собой выпуклую или вогнутую кривую. Однако в рабочем диапазоне изменения параметров эту кривую можно выпрямить, выразив 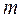через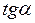 
.Итак имеем:
, 
, 
; 
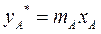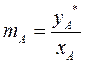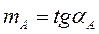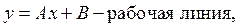
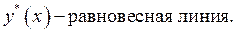
Дата добавления: 2016-05-25; просмотров: 869;