Установившееся истечение жидкости через
Большие отверстия
Малое отверстие характеризуется тем, что его размеры незначительны по сравнению с величиной напора над его геометрическим центром. Поэтому считают, что напор имеет постоянное значение для всех точек отверстия. Для большого отверстия, т. е. отверстия, размеры которого сравнимы с величиной напора в его центре, такое предположение не верно. Рассмотрим, например, истечение жидкости из большого отверстия в боковой стенке сосуда (рис. 10.3). В верхней точке такого отверстия, где напор жидкости меньше, скорость истечения меньше, чем в нижней точке отверстия, где напор жидкости больше.
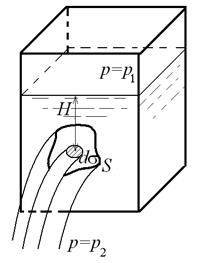
Рис. 10.3. Истечение жидкости через большое отверстие
При вычислении напора жидкости для большого отверстия применяют следующий приближенный прием. Считают, что каждый элемент 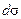 такого отверстия представляет собой малое отверстие, характеризуемое одним и тем же коэффициентом расхода
такого отверстия представляет собой малое отверстие, характеризуемое одним и тем же коэффициентом расхода 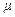 и скоростью истечения, соответствующей напору в центре этого малого отверстия. Таким образом, принимается, что расход
и скоростью истечения, соответствующей напору в центре этого малого отверстия. Таким образом, принимается, что расход 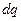 жидкости через элемент отверстия
жидкости через элемент отверстия 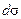 определяется формулой (10.9), полученной для малого отверстия:
определяется формулой (10.9), полученной для малого отверстия:
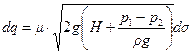 ,
,
а полный расход - интегралом от этого выражения, вычисленным по площади всего отверстия:
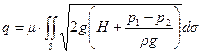 . (10.11)
. (10.11)
Пример 1. Истечение жидкости в атмосферу происходит через прямоугольное отверстие шириной 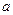 и высотой
и высотой 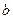 , расположенное на боковой стенке сосуда. Уровень свободной поверхности жидкости над верхней кромкой отвертстия равен
, расположенное на боковой стенке сосуда. Уровень свободной поверхности жидкости над верхней кромкой отвертстия равен 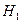 (рис. 10.4а). Требуется вычислить расход
(рис. 10.4а). Требуется вычислить расход 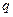 жидкости через это отверстие.
жидкости через это отверстие.
(переделать рис. 10.4б; 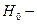 глубина центра круга!!!)
глубина центра круга!!!)
а. б.
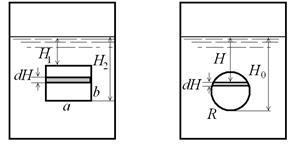
Рис. 10.4. Истечение жидкости через большие отверстия:
а) прямоугольное; б) круглое
Вычисление. В этом случае 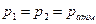 , так что
, так что 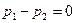 ,
, 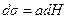 . На основании формулы (10.11) имеем:
. На основании формулы (10.11) имеем:
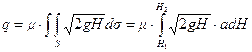
или
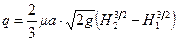 , (10.12)
, (10.12)
где 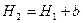 .
.
Пример 2. Истечение жидкости в атмосферу через круглое отверстие радиуса 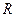 в боковой стенке сосуда. Уровень свободной поверхности жидкости над центром отвертстия равен
в боковой стенке сосуда. Уровень свободной поверхности жидкости над центром отвертстия равен 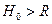 (рис. 10.4б). Требуется вычислить расход
(рис. 10.4б). Требуется вычислить расход 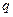 жидкости через это отверстие.
жидкости через это отверстие.
Вычисление. В этом случае 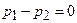 , так что
, так что 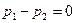 . Кроме того,
. Кроме того, 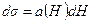 , где
, где 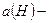 длина хорды круглого отверстия, находящаяся на глубине
длина хорды круглого отверстия, находящаяся на глубине 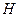 под свободной поверхностью. На основании формулы (10.11) имеем:
под свободной поверхностью. На основании формулы (10.11) имеем:
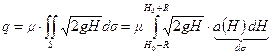 .
.
Сделав замену переменной интегрирования согласно формулам
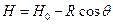 ,
, 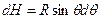 ,)
,)
где 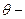 переменный угол (
переменный угол ( 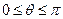 ), отсчитываемый от положительного направления вертикальной оси по часовой стрелке, так что рассаматриваемая хорда видна из центра круга под углом
), отсчитываемый от положительного направления вертикальной оси по часовой стрелке, так что рассаматриваемая хорда видна из центра круга под углом 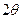 , получим:
, получим:
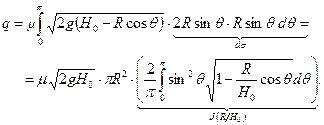 (10.13)
(10.13)
Значения интеграла 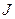 , стоящего в круглых скобках, зависит от отношения радиуса отверстия к глубине нахождениия его центра под свободной поверхностью жидкости. Однако в интервале
, стоящего в круглых скобках, зависит от отношения радиуса отверстия к глубине нахождениия его центра под свободной поверхностью жидкости. Однако в интервале 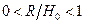 значений этого отношения, интеграл мало отличаются от единицы:
значений этого отношения, интеграл мало отличаются от единицы: 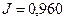 при
при 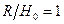 ;
; 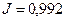 при
при 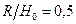 ;
; 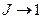 при
при 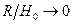 . Иными словами, относительная погрешность результатов, получаемых по формуле (10.13) от результатов, получаемых по формуле (10.8) для малого отверстия, составляет не более 4%.
. Иными словами, относительная погрешность результатов, получаемых по формуле (10.13) от результатов, получаемых по формуле (10.8) для малого отверстия, составляет не более 4%.
Дата добавления: 2016-05-16; просмотров: 1247;
