Истечение жидкости через малое отверстие в тонкой стенке
Рассмотрим основные закономерности истечения жидкости из сосуда через малое отверстие в его стенке, которую будем считать тонкой. Предположим также, что площадь 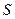 отверстия много меньше площади свободной поверхности жидкости в сосуде, вследствие чего скоростью опускания этой поверхности можно пренебречь, а само истечение считать установившимся.
отверстия много меньше площади свободной поверхности жидкости в сосуде, вследствие чего скоростью опускания этой поверхности можно пренебречь, а само истечение считать установившимся.
Воспользуемся уравнением Бернулли, применив его к жидкости, расположенной между сечениями 1 - 1 и 2 – 2, рис. 10.1. Первое из них совпадает со свободной поверхностью жидкости, второе выбрано в том месте вытекающей струи, где она становится цилиндрической. Подчеркнем, что в цилиндрической части струи скорости жидкости считаются равными друг другу, а давление вдоль сечения остается постоянным, равным его значению на поверхности струи. Имеем:
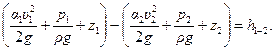 (10.1)
(10.1)
Здесь 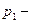 давление на свободной поверхности жидкости в сосуде;
давление на свободной поверхности жидкости в сосуде; 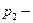 давление в той среде, в которую происходит истечение.
давление в той среде, в которую происходит истечение.
Скорость жидкости 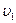 на свободной поверхности, в силу сделанного предположения, пренебрежимо мала:
на свободной поверхности, в силу сделанного предположения, пренебрежимо мала: 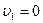 ; скорость истечения
; скорость истечения 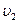 в дальнейшем будем обозначать просто
в дальнейшем будем обозначать просто 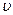 .
.
Потери 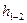 напора связаны с диссипацией механической энергии за счет сил внутреннего вязкого трения во всем объеме жидкости в сосуде, а также с дополнительными местными потерями, возникающими в самом отверстии. Если пренебречь первыми из них, так как скорости жидкости в сосуде невелики, то
напора связаны с диссипацией механической энергии за счет сил внутреннего вязкого трения во всем объеме жидкости в сосуде, а также с дополнительными местными потерями, возникающими в самом отверстии. Если пренебречь первыми из них, так как скорости жидкости в сосуде невелики, то 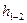 можно записать в следующем виде:
можно записать в следующем виде:
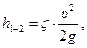 (10.2)
(10.2)
где 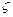 — коэффициент местного сопротивления отверстия, тогда
— коэффициент местного сопротивления отверстия, тогда
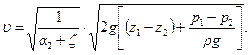 (10.3)
(10.3)
Введем в рассмотрение параметр 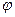 , называемый коэффициентом скорости и определяемый равенством
, называемый коэффициентом скорости и определяемый равенством
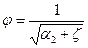 , (10.4)
, (10.4)
тогда равенство (10.3) можно переписать в следующем виде:
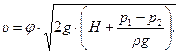 (10.5)
(10.5)
Формула служит для вычисления скорости истечения жидкости через малое отверстие при постоянном напоре. Коэффициент скорости 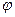 , входящий в эту формулу, зависит от числа Рейнольдса, которое в данном случае можно определить формулой
, входящий в эту формулу, зависит от числа Рейнольдса, которое в данном случае можно определить формулой
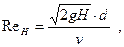
в которой 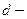 диаметр отверстия;
диаметр отверстия; 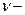 кинематическая вязкость жидкости;
кинематическая вязкость жидкости; 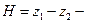 напор в середине отверстия;
напор в середине отверстия; 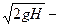 характерная скорость. Однако эксперименты показывают, что при больших
характерная скорость. Однако эксперименты показывают, что при больших 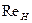 эта зависимость практически исчезает, и значение коэффициента
эта зависимость практически исчезает, и значение коэффициента 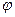 становится постоянным, близким к единице:
становится постоянным, близким к единице:
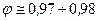 ;
;
В то же время для малых значений 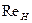 зависимость
зависимость 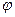 от
от 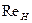 необходимо учитывать.
необходимо учитывать.
Если 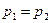 , т.е. давление на свободной поверхности жидкости и давление в среде, в которую эта жидкость вытекает, равны друг другу, то формула (10.5) упрощается и приобретает вид:
, т.е. давление на свободной поверхности жидкости и давление в среде, в которую эта жидкость вытекает, равны друг другу, то формула (10.5) упрощается и приобретает вид:
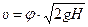 . (10.6)
. (10.6)
Если 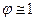 , то из (10.6) получается известная формула Торричелли:
, то из (10.6) получается известная формула Торричелли:
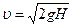 , (10.7)
, (10.7)
которая утверждает, что в рамках сделанных предположений скорость истечения жидкости из малого отверстия в сосуде равна скорости свободного падения материальной точки в пустоте с высоты 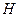 .
.
Вычислим расход жидкости. Поскольку скорости частиц в цилиндрической части струи одинаковы, то расход 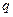 жидкости рассчитывается по следующей формуле:
жидкости рассчитывается по следующей формуле:
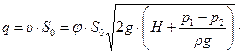 (10.8)
(10.8)
Если обозначить через 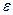 коэффициент сжатия струи, то площадь
коэффициент сжатия струи, то площадь 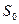 сжатого сечения струи жидкости и площадь отверстия
сжатого сечения струи жидкости и площадь отверстия 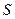 связаны: соотношением
связаны: соотношением 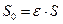 . Поэтому формула (10.8) может быть записана по-другому:
. Поэтому формула (10.8) может быть записана по-другому:
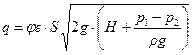 .
.
Произведение 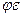 называют коэффициентом расхода и обозначают буквой
называют коэффициентом расхода и обозначают буквой 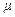 :
:
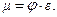
Окончательно формула для расхода жидкости через малое отверстие принимает вид:
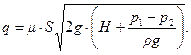 (10.9)
(10.9)
В общем случае коэффициент расхода, так же как и коэффициент скорости, зависит от режима истечения, определяемого числом Рейнольдса 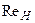 . При больших числах
. При больших числах 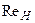 коэффициент
коэффициент 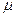 расхода изменяется незначительно. Так, например, для воды, нефтепродуктов, газового конденсата, многих нефтей и других и не слишком вязких жидкостей
расхода изменяется незначительно. Так, например, для воды, нефтепродуктов, газового конденсата, многих нефтей и других и не слишком вязких жидкостей 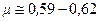 . Для вычисления коэффициента
. Для вычисления коэффициента 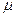 расхода при
расхода при 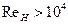 проф. А.Д. Альтшуль предложил эмпирическую формулу
проф. А.Д. Альтшуль предложил эмпирическую формулу
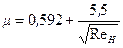 . (10.10)
. (10.10)
Дата добавления: 2016-05-16; просмотров: 1737;
