Определение времени опорожнения резервуаров
Закономерности истечения вязкой несжимаемой жидкости через отверстия в стенках сосудов имеют важное приложение к задачам практики в нефтяной промышленности. Это, прежде всего, задачи о времени опорожнения всевозможных резеруаров и подвиженых емкостей.
Покажем, как, например, вычислить время истечения жидкости из резервуара, форма которого известна. Рассмотрим случай, когда жидкость вытекает в атмосферу через отверстие площадью 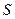 в дне сосуда. Давление на свободной поверхности принимается равным атмосферному (рис. 10.9).
в дне сосуда. Давление на свободной поверхности принимается равным атмосферному (рис. 10.9).
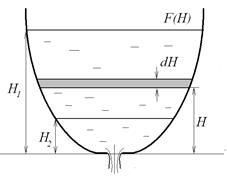
Рис. 10.9. Расчет времени опорожнения резервуара
Движение жидкости в рассматриваемом случае является неустановившимся, т. к. напор изменяется с течением времени, а, следовательно, меняется и расход вытекающей жидкости. В тех случаях, когда истечение жидкости происходит медленно, можно пользоваться гипотезой последовательной смены стационарных состояний.
Смысл этой гипотезы состоит в том, что если уровень жидкости в сосуде меняется медленно, то истечение жидкости в течение каждого интервала времени можно считать установившимся и пользоваться формулой, полученной для расхода жидкости при постоянном напоре
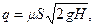
полагая в ней величину 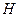 равной значению напора в данный момент времени. Таким образом:
равной значению напора в данный момент времени. Таким образом:
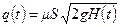 . (10.22)
. (10.22)
За малый интервал 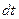 времени уровень жидкости в сосуде уменьшится на величину
времени уровень жидкости в сосуде уменьшится на величину 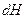 . Если площадь свободной поверхности жидкости в сосуде обозначить через
. Если площадь свободной поверхности жидкости в сосуде обозначить через 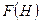 , то объем
, то объем 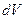 жидкости, соответствующий уменьшению уровня жидкости на величину
жидкости, соответствующий уменьшению уровня жидкости на величину 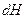 , дается выражением
, дается выражением
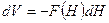 , (10.23)
, (10.23)
причем знак минус в этой формуле берется потому, что 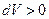 при
при 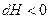 .
.
Объем 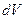 жидкости, вытекающей из сосуда, можно выразить по-другому, через расход
жидкости, вытекающей из сосуда, можно выразить по-другому, через расход 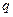 :
:
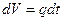 .
.
Подставляя вместо 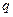 его выражение, согласно, (10.22), получаем
его выражение, согласно, (10.22), получаем
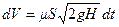 . (10.24)
. (10.24)
Сравнивая (10.23) и (10.24), находим:
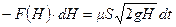 ,
,
или
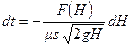 . (10.25)
. (10.25)
Для определения времени опорожнения резервуара от уровня 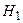 до уровня
до уровня 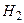 проинтегрируем обе части уравнения (10.25): левую часть по
проинтегрируем обе части уравнения (10.25): левую часть по 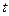 от 0 до
от 0 до 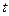 и правую часть по H от
и правую часть по H от 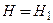 до
до 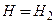 . Получим:
. Получим:
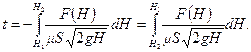 (10.26)
(10.26)
Коэффициент 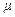 , входящий в эту формулу, зависит, вообще говоря, от числа Рейнольдса
, входящий в эту формулу, зависит, вообще говоря, от числа Рейнольдса 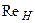 , которое определяется переменной во времени величиной напора
, которое определяется переменной во времени величиной напора 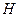 . Поэтому в общем случае интеграл в формуле (10.20) следует вычислять с учетом зависимости
. Поэтому в общем случае интеграл в формуле (10.20) следует вычислять с учетом зависимости 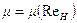 . Однако для многих, не слишком вязких жидкостей, величина коэффициента расхода
. Однако для многих, не слишком вязких жидкостей, величина коэффициента расхода 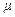 остается постоянной на протяжении всего времени истечения. Рассмотрим случай, когда коэффициент расхода
остается постоянной на протяжении всего времени истечения. Рассмотрим случай, когда коэффициент расхода 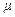 постоянен, тогда:
постоянен, тогда:
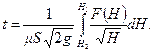 (10.27)
(10.27)
Если резервуар имеет постоянную площадь сечения 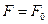 (например, призматический резервуар, рис.10.10), то из (10.27) получим:
(например, призматический резервуар, рис.10.10), то из (10.27) получим:
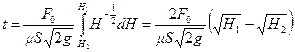 .
.
В частности, время 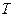 полного опорожнения призматического резервуара от уровня
полного опорожнения призматического резервуара от уровня 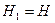 до уровня
до уровня 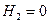 определится по формуле:
определится по формуле:
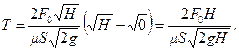 (10.28)
(10.28)
В формуле (10.28) в числителе стоит удвоенный объем резервуара, а в знаменателе — расход жидкости из отверстия при постоянном напоре 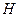 , поэтому
, поэтому
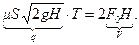
Таким образом, если умножить расход при постоянном напоре на время истечения, то получим удвоенный объем резервуара. Следовательно, для истечения количества жидкости, равного объему резервуара, при переменном уровне требуется время в два раза больше того, за которое вытекает то же количество жидкости при постоянном напоре, равном начальной высоте уровня жидкости в резервуаре.
Пример.Задача об определении времени истечения жидкости из цистерны. Требуется найти время опорожнения круглой горизонтальной цистерны с длиной 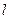 и радиусом
и радиусом 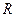 , рис. (10.10) и рис. (10.11).
, рис. (10.10) и рис. (10.11).
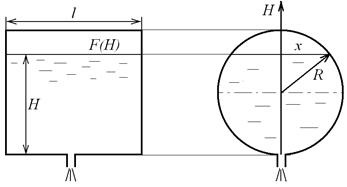
| Рис. 10.10. Призматический резервуар | Рис. 10.11. Цилиндрическая цистерна |
Площадь 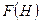 опускающейся свободной поверхности жидкости в цистерне записывается в виде
опускающейся свободной поверхности жидкости в цистерне записывается в виде
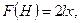 где
где 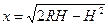 ,
,
тогда
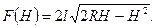 (10.29)
(10.29)
Определим время 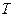 полного опорожнения цистерны, при котором уровень
полного опорожнения цистерны, при котором уровень 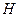 жидкости будет уменьшаться от
жидкости будет уменьшаться от 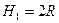 до
до 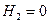 . Из общей формулы (10.26) с учетом выражения (10.29) для
. Из общей формулы (10.26) с учетом выражения (10.29) для 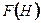 получим:
получим:
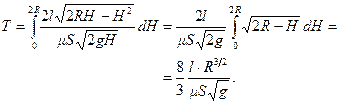 . .(10.30)
. .(10.30)
Дата добавления: 2016-05-16; просмотров: 6226;
