Жидкости с тепловым расширением

То, что различные среды при нагревании расширяются, а при охлаждении сжимаются, учитываются в модели жидкости с объемным расширением. В этой модели плотность 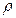есть функция от температуры 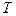, так что :

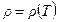, (2.3)

в которой 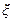( 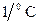) - коэффициент объемного расширения, а 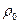и номинальные плотность и температура жидкости. Для воды, нефти и нефтепродуктов значения коэффициента 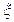приведены в таблице 2.1.

Из формулы (2.3) следует, в частности, что при нагревании, т.е. в тех случаях, когда , 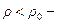жидкость расширяется; а в тех случаях, когда 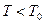, 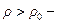жидкость сжимается.

Таблица 2.1

Коэффициент 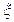объемного расширения

Плотность 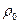, кг/м3	Коэффициент 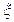, 1/ 0C
700-719	0,001225
720-739	0,001183
740-759	0,001118
760-779	0,001054
780-799	0,000995
800-819	0,000937
820-839	0,000882
840-859	0,000831
860-880	0,000782

Пример 1. Плотность 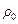бензина при 20⁰С равна 745 кг/м³. Какова плотность этого же бензина при температуре 10⁰С?

Решение.Используя формулу (2.3) и таблицу 1, имеем:

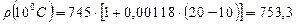кг/м³, т.е. эта плотность увеличилась на 8,3 кг/м³.

Используется также модель жидкости, учитывающей как барическое, так и тепловое расширение. В этой модели 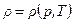, причем справедливо следующее уравнение состояния:

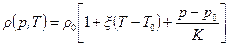. (2.4)

Здесь .

Пример 2. Плотность бензина 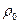при 20⁰С и атмосферном давлении ( МПа) равна 745 кг/м³. Какова плотность этого же бензина при температуре 10⁰С и давлении 6,5 МПа?

Решение. Используя формулу (2.4) и таблицу 2.1, имеем:

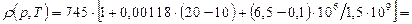
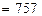кг/м³, т.е. эта плотность увеличилась на 12 кг/м³.