Несжимаемая жидкость

В тех случаях, когда изменениями плотности у частиц жидкости можно пренебречь, используют модель так называемой несжимаемой жидкости. Плотность каждой частицы такой гипотетической жидкости остается постоянной в течение всего времени движения (иными словами, полная производная 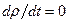), хотя она может быть и разной у разных частиц (как, например, у водонефтяных эмульсий). Если же несжимаемая жидкость однородна, то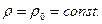

Подчеркнем, что несжимаемая жидкость представляет собой лишь модель, которую можно использовать в тех случаях, когда изменения 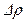плотности жидкости много меньше значения самой плотности 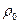, так что .

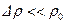Вязкость жидкости

Если слои жидкости движутся друг относительно друга, то между ними, возникают силы трения. Эти силы называют силами вязкого трения,а свойство сопротивления относительному движению слоев - вязкостью жидкости.

Пусть, например, слои жидкости движутся так, как показано на рис. 2.1.

Рис. 2.1. К определению вязкого трения

Здесь 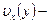распределение скоростей в потоке, а 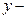направление нормали к площадке 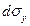. Верхние слои движутся быстрее нижних, поэтому со стороны первых действует сила трения, увлекающая вторые вперед по ходу течения, а со стороны нижних слоев действует сила трения, тормозящая движение верхних слоев. Величина 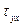- это x-составляющая силы трения между слоями жидкости, разделенными площадкой с нормалью y, рассчитанная на единицу площади.

Если ввести в рассмотрение производную 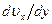, то она будет характеризовать скорость сдвига, т.е. разность скоростей слоев жидкости, рассчитанную на единицу расстояния между ними. Оказывается, что для многих жидкостей справедлив закон, согласно которому касательное напряжение 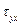между слоями пропорционально разности скоростей этих слоев, рассчитанной на единицу расстояния между ними:

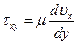, (2.5)

Смысл этого закона понятен: чем больше относительная скорость слоев жидкости (скорость сдвига), тем больше сила трения между слоями.

Жидкость, для которой справедлив закон (2.5) называют ньютоновской вязкой жидкостью. Многие капельные жидкости удовлетворяют этому закону, однако, входящий в него коэффициент пропорциональности оказывается различным для различных жидкостей. Говорят, что такие жидкости являются ньютоновскими, но с разной вязкостью.

Коэффициент пропорциональности 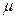, входящий в закон (2.5), называют коэффициентом динамической вязкости.

Размерность этого коэффициента такова

.

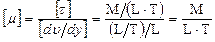В системе СИ 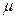измеряется в 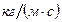и выражается в Пуазах (Пз). Эта единица введена в честь Жана Луи Мари Пуазейля, (1799-1869) – выдающегося французского врача и физика, много сделавшего для изучения движения жидкости (в частности, крови) в трубе.

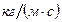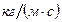Пуаз определяется так: 1 Пз = 0,1 . Чтобы составить представление о величине 1 Пз, заметим, что коэффициент динамической вязкости воды в сто раз меньше 1 Пз, т.е. 0,01 Пз = 0,001 = 1 санти Пуаз. Вязкость бензинов составляет 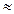0,4-0,5 Пз, дизельных топлив 4 – 8 Пз, нефти – 5-30 Пз и больше.

Для описания вязких свойств жидкости важен также другой коэффициент, являющийся отношением коэффициента динамической вязкости 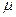к плотности жидкости, а именно 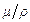. Этот коэффициент обозначают 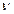и называют коэффициентом кинематической вязкости.

Размерность коэффициента кинематической вязкости такова:

[ ] = .

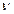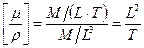В системе СИ 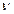измеряется м²/с и выражается Стоксами (Джордж Габриель Стокс (1819-1903) – выдающийся английский математик, физик и гидромеханик):

1 Ст = 10^-4 м²/с.

При таком определении кинематической вязкости для воды имеем:

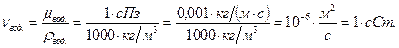
Иными словами, единицы измерения для динамической и кинематической вязкости выбраны таким образом, чтобы и та, и другая для воды была бы равна 0,01 единицы: 1 сПз в первом случае и 1 сСт – во втором.

Для справки укажем, что кинематическая вязкость бензина составляет примерно 0,6 сСт; дизельного топлива - 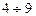сСт; маловязкой нефти - 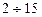сСт и т.д.

Зависимость вязкости от температуры. Вязкость многих жидкостей - воды, нефти и почти всех нефтепродуктов - зависит от температуры. При повышении температуры вязкость уменьшается, при понижении - увеличивается. Для расчета зависимости вязкости, например, кинематической 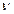от температуры 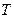используются различные формулы, в том числе и формула О.Рейнольдса - П.А.Филонова

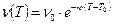, (2.6)

где 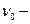кинематическая вязкость жидкости при температуре 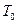, а 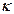(1/K) - опытный коэффициент. Формула (2.6) отражает тот факт, что с изменением температуры вязкость жидкости изменяется экспоненциально.

Для того чтобы воспользоваться формулой (2.6), необходимо знать либо коэффициент 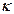, либо вязкость 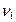той же жидкости еще при одной температуре 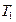. Тогда этот коэффициент находится по формуле

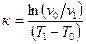. (2.7)

Пример. Кинематическая вязкость летнего дизельного топлива при температуре + 20⁰С равна 5 сСт, а при температуре 0⁰С она увеличивается до 8 сСт. Какая вязкость того же дизельного топлива при температуре + 10⁰С?

Решение. По формуле (2.7) рассчитываем коэффициент 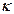: 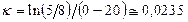. По формуле (2.6) находим искомую вязкость: 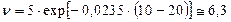сСт.

Идеальная жидкость

Если силы трения между слоями жидкости много меньше нормальных (сдавливающих) сил, то вводят модель так называемой идеальной жидкости. В этой модели считается, что касательные силы трения между частицами, разделенными площадкой, отсутствуют 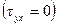и при течении жидкости, а не только в состоянии покоя(см. в п. 1.9 определение жидкости). Такая схематизация жидкости оказывается весьма полезной в тех случаях, когда касательные составляющие сил взаимодействия (силы трения) много меньше их нормальных составляющих (сил давления). В других же случаях, когда силы трения сопоставимы с силами давления или даже превосходят их, модель идеальной жидкости оказывается неприменимой.

Поскольку в идеальной жидкости существуют только нормальные напряжения, то вектор напряжения 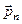на любой площадке с нормалью 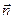перпендикулярен этой площадке 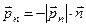. Повторяя построения п.1.9, можно заключить, что в идеальной жидкости все нормальные напряжения равны по величине и отрицательны ( 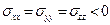). Следовательно, в идеальной жидкости существует параметр 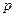, называемый давлением:, 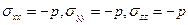, а матрица напряжений имеет вид:

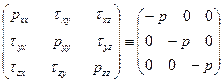. (2.8)