Постоянные нагрузки на магистральный трубопровод.
Постоянные нагрузки действуют в течение всего срока строительства и эксплуатации трубопровода.
· Собственный вес трубопровода – вес погонного метра трубы вычисляется по формуле
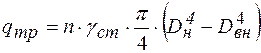 , (8.2)
, (8.2)
где 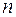 – коэффициент надежности по нагрузке,
– коэффициент надежности по нагрузке, 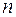 =1,1;
=1,1;
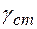 - удельный вес стали,
- удельный вес стали, 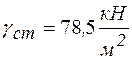 ;
;
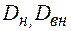 - наружный и внутренний диаметры трубы.
- наружный и внутренний диаметры трубы.
· Вес одного метра изоляционного покрытия
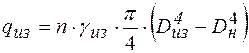 , (8.3)
, (8.3)
где 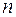 = 1,1 - коэффициент надежности по нагрузке;
= 1,1 - коэффициент надежности по нагрузке;
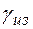 - удельный вес изоляции;
- удельный вес изоляции;
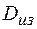 - наружный диаметр изоляции.
- наружный диаметр изоляции.
Для предварительных расчетов ориентировочно можно принимать вес изоляции равным 10% от веса трубы.
· Давление грунта на единицу длины трубопровода
 , (8.4)
, (8.4)
где 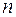 = 1,2 – коэффициент надежности по давлению грунта;
= 1,2 – коэффициент надежности по давлению грунта;
 - удельный вес грунта;
- удельный вес грунта;
 - средняя глубина заложения оси трубопровода.
- средняя глубина заложения оси трубопровода.
· Гидростатическое давление воды на единицу длины трубопровода, определяемое высотой столба жидкости над подводным трубопроводом
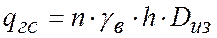 , (8.5)
, (8.5)
где 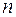 =1,0 – коэффициент надежности гидростатического давления воды;
=1,0 – коэффициент надежности гидростатического давления воды;
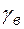 - удельный вес воды с учетом засоленности и наличия взвешенных частиц;
- удельный вес воды с учетом засоленности и наличия взвешенных частиц;
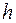 – высота столба воды над рассматриваемой точкой трубы;
– высота столба воды над рассматриваемой точкой трубы;
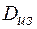 – диаметр изолированной и футерованной трубы.
– диаметр изолированной и футерованной трубы.
· Выталкивающая сила воды, приходящаяся на единицу длины трубопровода полностью погруженного в воду
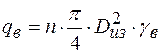 , (8.6)
, (8.6)
где 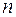 = 1,0 – коэффициент надежности гидростатического давления воды.
= 1,0 – коэффициент надежности гидростатического давления воды.
Если магистральный трубопровод проложен на участках грунтов, которые при обводнении переходят в жидкопластическое состояние, то в формуле (8.16) вместо удельного веса воды принимают удельный вес разжиженного грунта, определяемый по результатам инженерных изысканий.
· Предварительное напряжение, создаваемое за счет упругого изгиба при повороте оси трубопровода.
Определим деформации и напряжения в поперечных сечениях изогнутой трубы (рисунок 22).

Рисунок 22.
Рассмотрим деформацию волокна трубы с координатой y. Относительное удлинение волокна 

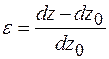 , (8.7)
, (8.7)
где  - длина выделенного элемента трубы до деформации;
- длина выделенного элемента трубы до деформации;
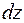 - длина элемента после деформации.
- длина элемента после деформации.
После того, как трубопровод получил упругий изгиб его деформации и напряжения являются функцией радиуса кривизны 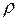
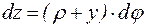 ;
; 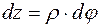 .
.
После подстановки этих значений в выражение (8.7) получаем выражение деформаций трубы через её радиус кривизны
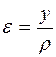 . (8.8)
. (8.8)
Напряжения получаем с учетом закона Гука
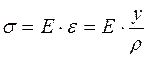 . (8.9)
. (8.9)
Для точек наиболее удаленных от оси трубы  . В этих точках соответственно возникают наибольшие растягивающие и наибольшие сжимающие напряжения
. В этих точках соответственно возникают наибольшие растягивающие и наибольшие сжимающие напряжения
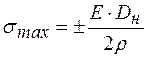 . (8.10)
. (8.10)
Дата добавления: 2016-04-22; просмотров: 1257;
