Поняття логічного слідування
Основним завданням математичної логіки є мистецтво правильних умовиводів із правильних посилок, тобто мистецтво міркування.
Одержання нових знань із уже наявних, виражених у формі висловлення, називається умовивід або міркування. При цьому вихідні висловлення, твердження називаються гіпотезами або посилками, а одержувані – висновком або логічним наслідком.
Правильним умовиводом називається таке міркування, висновок (логічний наслідок) якого є істинний щораз, коли істинні його гіпотези.
Умовивід представляють у вигляді 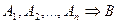 , де
, де
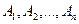 ‑ гіпотези,
‑ гіпотези, 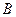 ‑ висновок, а символ “
‑ висновок, а символ “ 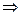 ” означає “отже”.
” означає “отже”.
Формула B(p1,p2,...,pn) є логічним слідуванням формули A(p1,p2,...,pn), якщо B приймає значення 1 для всіх тих наборів значень пропозиційних змінних, для яких формула A істинна (тобто приймає значення 1); позначатимемо це AÞB.
Очевидно, що дві формули A і B є рівносильними тоді і тільки тоді, коли кожна з них є логічним слідуванням іншої, тобто A=B тоді і тільки тоді, коли AÞB і BÞA.
Формула B(p1,p2,...,pn) є логічним слідуванням формул 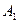 (p1,p2,...,pn), … ,
(p1,p2,...,pn), … , 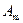 (p1,p2,...,pn), якщо B приймає значення 1 для всіх тих наборів значень пропозиційних змінних, для яких всі формули
(p1,p2,...,pn), якщо B приймає значення 1 для всіх тих наборів значень пропозиційних змінних, для яких всі формули 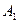 , … ,
, … , 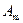 приймають значення 1; позначатимемо це
приймають значення 1; позначатимемо це 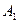 , … ,
, … , 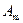 ÞB.
ÞB.
Теорема. Формула B(p1,p2,...,pn) є логічним слідуванням формул 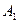 (p1,p2,...,pn), … ,
(p1,p2,...,pn), … , 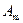 (p1,p2,...,pn) тоді і тільки тоді, коли тавтологією є формула
(p1,p2,...,pn) тоді і тільки тоді, коли тавтологією є формула 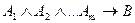 , тобто
, тобто
якщо 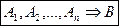 , то
, то 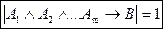 (тавтологія)
(тавтологія)
Правильність (або істинність) побудованого умовиводу можна перевірити двома способами, а саме:
за допомогою таблиці істинності можна показати, що висновок істинний щораз, коли істинні гіпотези; за допомогою логічних правил можна довести істинність висновку.
Властивості логічного слідування
- Якщо
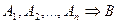 і
і 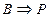 , то
, то 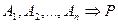 (властивість транзитивності).
(властивість транзитивності). - Якщо
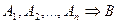 і Р – довільна формула алгебри висловлень, то
і Р – довільна формула алгебри висловлень, то 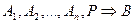
(приєднання довільної формули алгебри висловлень до числа посилок не порушує даного логічного слідування).
- Якщо
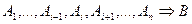 і
і 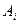 є тавтологією, то
є тавтологією, то 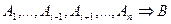
(вилучення з числа посилок формули, яка є тавтологією, не порушує даного логічного слідування)
Схеми логічного слідування (правила виведення) в логіці висловлювань
1. Modus ponens (МР) (правило висновку): p 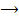 q, p
q, p 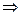 q
q
2. Modus tollens (МТ): p 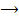 q,
q, 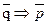 (tollens - заперечувальний)
(tollens - заперечувальний)
3. Введення диз’юнкції: p 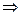 p
p 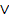 q;
q;
4. Вилучення кон’юнкції: p, q 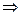 p;
p;
Похолоднішало і почав падати дощ, отже похолоднішало.
5. Правило силогізму: p 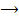 q, q
q, q 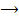 r
r 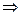 p
p 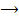 r;
r;
Якщо сьогодні падатиме дощ, то сьогодні ми не поїдемо на пікнік. Якщо ми не поїдемо на пікнік сьогодні, то поїдемо завтра. Отже, якщо сьогодні падатиме дощ, то поїдемо на пікнік завтра.
6. Диз’юнктивний силогізм: 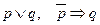 ;
;
7. Резолюція: 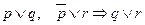 .
.
Множина формул 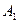 (p1,p2,...,pn), … ,
(p1,p2,...,pn), … , 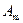 (p1,p2,...,pn), називається сумісною (несуперечною), якщо існує такий розподіл істинісних значень p1,p2,...,pn, , при якому
(p1,p2,...,pn), називається сумісною (несуперечною), якщо існує такий розподіл істинісних значень p1,p2,...,pn, , при якому 
Множина формул, яка не є сумісною, називається суперечною.
Множина формул 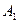 (p1,p2,...,pn), … ,
(p1,p2,...,pn), … , 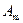 (p1,p2,...,pn), називається сумісною(суперечною) тоді і тільки тоді, коли хоча б на одному наборі (на всіх наборах) значень p1,p2,...,pn,, всі формули (хоча б одна з формул) набувають (набуває ) значення 1 (0).
(p1,p2,...,pn), називається сумісною(суперечною) тоді і тільки тоді, коли хоча б на одному наборі (на всіх наборах) значень p1,p2,...,pn,, всі формули (хоча б одна з формул) набувають (набуває ) значення 1 (0).
Теорема Якщо Г – суперечна множина формул логіки висловлювань, то для довільної формули А має місце слідування 
Дата добавления: 2016-04-22; просмотров: 1841;
